Criteri di stabilità

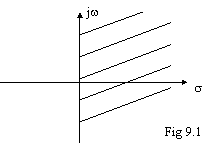
In generale, dato un sistema che presenta una funzione di trasferimento F(s), dove s=s+jw, condizione necessaria affinché il sistema sia stabile è che i poli di F(s) non compaiono nel semipiano positivo (zero compreso) delle s

			Limitando il discorso agli amplificatori, vediamo ora un criterio per determinare la loro stabilità.

9.1.1. Criterio di Nyquist

Il sistema che prendiamo in analisi presenta dunque un anello di reazione e una funzione di trasferimento con questa forma:

Facciamo l'ipotesi che i blocchi G e H siano in partenza stabili, in altre parole non abbiano poli per s³

Questo significa che neanche il denominatore di G_F

presenta dei poli.

Immaginando di scomporre M(s) in numeratore N(s) e denominatore D(s), abbiamo che, per le ipotesi fatte, D(s) non presenta poli per s³0. Quindi non resta che stabilire se N(s) presenta degli zeri, oppure, equivalentemente, se M(s) presenta degli zeri.

In conclusione si ha stabilità quando 1+GH non presenta zeri (né poli per ipotesi) per s³

Per determinare il numero e la posizione dei poli possiamo utilizzare un risultato della teoria delle funzioni analitiche che mette in relazione il comportamento di F(s) con il numero dei suoi zeri e dei suoi poli.

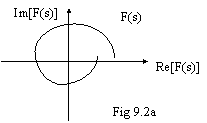
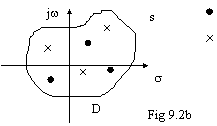
Con riferimento alle . 9.2a e 9.2b, la quantità è uguale al numero di inviluppi di F(s) intorno all'origine (il verso di rotazione dipende da quale delle due quantità è maggiore). Se il dominio D scelto non comprende poli e zeri, oppure se il numero dei poli è uguale al numero degli zeri, F(s) non inviluppa l'origine (inviluppare l'origine=compiere un giro completo intorno all'origine).

Per le considerazioni precedenti, sappiamo che la nostra F(s) non presenta poli per s³0; di conseguenza, qualunque contorno contenuto nel semipiano s³0 noi consideriamo, la nostra F(s) non dovrebbe inviluppare l'origine. Se ciò accade significa che esiste almeno uno zero nel semipiano s³0 e quindi il sistema è instabile. Il contorno più grande che possiamo considerare è quello che contiene tutto il semipiano s³0, quindi:

In definitiva, noi dobbiamo studiare la quantità 1+G(s)H(s) nell'intorno dell'origine; se questa funzione contorna l'origine il sistema è instabile, altrimenti è stabile.

Equivalentemente, ed è quello che faremo, possiamo studiare la funzione G(s)H(s) nell'intorno di 1. Inoltre, siccome G(s)H(s) è a coefficienti reali, è simmetrica rispetto all'asse reale, quindi possiamo limitare lo studio all'intervallo [0,+¥

Per fare questo utilizziamo un diagramma polare ( 9.3b), su cui disegniamo, al variare di jw da 0 a +¥, il modulo e la fase di GH.

				9.3b

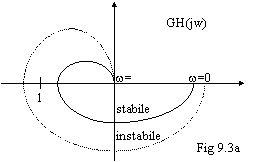
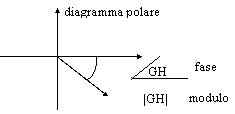
In ura 9.3a compaiono due forme tipiche di GH(jw) per gli amplificatori. Vediamo che la curva che passa tra 0 e 1 (non contorna l'1) indica un sistema stabile, mentre la curva che passa oltre l'1 indica un sistema instabile.

9.1.1.1. Margine di guadagno e di fase

Il criterio che abbiamo visto è teorico. Nella pratica occorre avere un margine maggiore per decidere se un sistema è stabile oppure no.

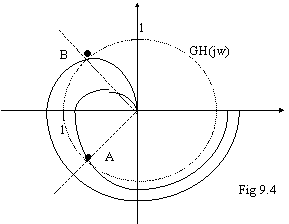
			Consideriamo la fase di GH quando |GH|=1; nell'esempio di 9.4, la curva che passa internamente a 1 interseca la circonferenza di raggio 1 nel punto A, e qui la fase a vale circa 225°; la curva che passa esternamente a 1 interseca la circonferenza nel punto B, e qui la fase a vale circa 135°.

Definizione: Margine di fase = fase di GH (quando |GH|=1) ­- 180°

Nell'esempio il margine di fase della prima curva è 225°-l80°=45°, il margine di fase della seconda curva è 135°-l80°=-45°.

Il criterio teorico, tradotto secondo il margine di fase, dice:

se margine di fase > 0 Þ sistema stabile

se margine di fase < 0 Þ sistema instabile

Il criterio pratico dice:

se margine di fase ³ Þ sistema "ingegneristicamente" stabile

se margine di fase < 45° Þ sistema "ingegneristicamente" instabile

Definizione: Margine di guadagno (in dB) = |GH| quando fase di GH=180°

Nell'esempio, quando la fase è 180°, la prima curva ha modulo <1, quindi il margine di guadagno è >0, la seconda ha modulo >1, quindi il margine di guadagno è <0.

Il criterio teorico, tradotto secondo il margine di guadagno, dice:

se margine di guadagno > 0 Þ sistema stabile

se margine di guadagno < 0 Þ sistema instabile

9.1.2 Criterio di Bode

Il criterio di Bode discende da quello di Nyquist ma è più semplicistico. Nonostante questo, per noi va benissimo, perché limitiamo il nostro studio agli amplificatori.

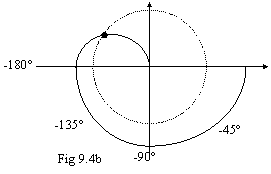
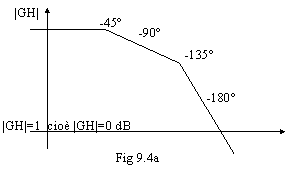
Esiste una precisa corrispondenza tra il grafico di 9.4a e quello di . 9.4b. A destra abbiamo il comportamento modulo/fase di GH al variare di jw, tracciato su un diagramma polare, a sinistra abbiamo il comportamento del modulo di GH, tracciato su un diagramma di Bode. Al diminuire della fase (da -45° a -l80°) il modulo diminuisce fino a diventare minore di 1: questo accade a destra quando la curva interseca la circonferenza unitaria, a sinistra quando la curva passa al di sotto dell'asse X (0 dB).

Il criterio di Nyquist ci dice che una curva di questo tipo ( 9.4b) indica instabilità del sistema. A sinistra ( 9.4a) osserviamo che la curva taglie l'asse X con una pendenza di -40dB/decade.

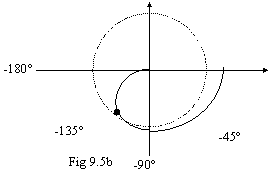
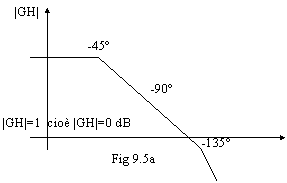
In questo secondo caso il criterio di Nyquist ci dice che il sistema è stabile, perché la curva non contorna l'1. In 9.5a osserviamo che la curva taglia l'asse X (cioè |GH| diventa minore di 1, o minore di 0dB) quando la sua pendenza è pari a -20dB/decade. In . 9.5b notiamo che la curva taglia la circonferenza unitaria con un margine di fase maggiore di 45°, viene quindi rispettato la condizione "pratica" di stabilità.

Da queste considerazioni si può dedurre che la curva del modulo di GH non deve tagliare l'asse X con un'inclinazione superiore a -20 dB/decade, altrimenti il sistema è (praticamente) instabile. Il caso estremo si ha quando il margine di fase è proprio 45°, cioè quando la curva a destra taglia la circonferenza unitaria proprio a -l35° (cioè a 225°). Questo caso è rappresentato dai grafici di 9.6 a e 9.6b; a  sinistra abbiamo che l'inclinazione della curva cambia proprio nel punto di intersezione con l'asse X.

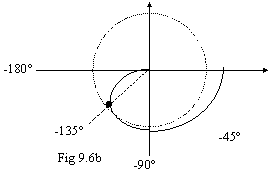
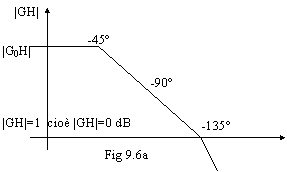
Chiamando a il polo a sinistra e b il polo a destra, quando si verifica questa condizione abbiamo che la seguente relazione è vera:

Infatti il segmento di curva che unisce i due poli ha un'inclinazione di  -20dB/decade, cioè è inclinata di 45 gradi, quindi la distanza che separa i due poli sull'asse X è pari alla distanza che li separa sull'asse Y, distanza pari a G₀H.

Abbiamo visto in precedenza che quando questa relazione è soddisfatta il sistema presenta i seguenti valori:

Q=1, k=1/2 e w a