Tecniche di risoluzione di circuiti - Connessione serie, Connessione parallelo, Partitore di tensione, Partitore delle correnti, Trasformazioni triang

Tecniche di risoluzione di circuiti

Connessione serie

Sono detti connessi in serie dei bipoli collegati tramite i loro morsetti ed attraversati dalla stessa intensità di corrente.

Per la legge di Kirchhoff per la tensione, posso dire che la tensione totale sui bipoli in serie è la somma delle singole tensioni dei bipoli. Se applico questo ai resistori ottengo:

v = v₁ + v₂ + + v_n

v₁ = R₁i v₂ = R₂i v_n = R_ni

E' possibile ora applicare il principio di equivalenza: se due elementi diversi hanno le stesse caratteristiche, la rete non si accorge della differenza. Da questo ricavo che una serie di n resistori equivale ad un unico resistore la cui resistenza è la somma delle singole resistenze.

Connessione parallelo

Ho una connessione di n-poli di tipo parallelo se ai loro morsetti osservo la stessa tensione.

Procedo come prima ma con le correnti.

i = i₁ + i₂ + + i_n

i₁ = G₁v i₂ = G₂v i_n = G_nv

Da qui si ricavano agevolmente due formule:

- , in cui il termine fra parentesi è detto conduttanza equivalente parallelo;

- , in cui il termine fra parentesi è detto resistenza equivalente serie;

E' possibile ottenere anche la resistenza equivalente parallelo:

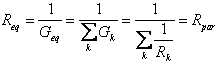
Nel caso in cui il parallelo sia composto di sole due resistenze ho la semplice formula , che nel caso di due resistenze uguali diventa .

La resistenza equivalente è sempre minore di tutte le resistenze considerate. L'operatore parallelo è associativo e commutativo.

Partitore di tensione

Nel caso di una connessione serie di resistori, data la tensione totale, è possibile trovare le tensioni parziali con un semplice partitore di tensione.

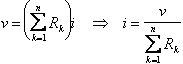, da cui .

Partitore delle correnti

Lo stesso ragionamento si può fare per le correnti che percorrono un parallelo.

Nel caso di due sole resistenze, si ricava, con dei semplici passaggi algebrici,

Trasformazioni triangolo - stella e viceversa

Sono delle tecniche che si usano quando si hanno più resistori in serie, ma la serie non è una serie propriamente detta o un parallelo. Si può dimostrare che per ogni tipo di connessione, si può convertire la rete in un'altra equivalente conentenente solo paralleli o serie propriamente dette tramite le conversioni stella o triangolo.

La conversione da una all'altra si ha con delle formule molto complesse.

La difficoltà maggiore sta nel riuscire a distinguere le conurazioni stella e triangolo. Per svolgere agevolemnte il compito ci si riferisce ai morsetti e li si etichetta. Si ha una stella se da ogni morsetto parte una resistenza e tutte le resistenze si raccolgono in un solo punto. Si ha un triangolo se fra ogni coppia di morsetti si trova una resistenza.

Come già detto, le formule di conversione del caso generale sono lunghe e difficili da ricordare ed applicare. La conversione è utile nel caso in cui le resistenze abbiano lo stesso valore. In questo caso R_t = 3R_s.

E' semplice la verifica della formula:

R_{eq s} = 2R_s R_{eq t} = (2 / 3)R_t ed eguagliando 2R_s = (2 / 3)R_t da cui la tesi.

Teorema di Millman - Brontolo

Un circuito in cui si possono isolare due nodi connessi da rami in cui si hanno serie di generatori ideali di tensione con resistori e generatori ideali di corrente con resistori è un circuito di tipo Millman. La differenza di tensione fra i due nodi si ottiene facilmente con una formula. Etichettando come 1 e 2 i nodi isolati, si scrive, indifferentemente, un'equazione di Kirchhoff per le correnti. Avendo m rami con generatori di tensione e n rami con generatori di corrente si ha:

i_e1 + i_e2 + + i_em + i_a1 + i_a2 + + i_an = 0

Se si analizza un ramo contenente un generatore di tensione si ottiene  da cui .

Con una serie di agevoli passaggi si ha

I valori da inserire nelle sommatorie sono positivi se i generatori sono equiversi con la v che si vuole ottenere. Le resistenze associate ai generatori di corrente non influenzano la v. Se un generatore di tensione è nullo, ovvero ho un ramo con solo una resistenza, si conta la resistenza nella sommatoria a denominatore nella formula.

Principio di sovrapposizione degli effetti

Si dicono reti lineari quelle reti che contengono solo elementi con caratteristiche lineari. In ogni rete lineare, ogni grandezza interna è sempre combinazione lineare di tutte le sorgenti all'interno della rete. Il contributo di ciascun generatore è detto effetto, e può essere calcolato "spegnendo" gli altri generatori.

Si può così dire che, spegnendo ad uno ad uno i generatori e lasciandone solo uno acceso, si calcolano i singoli effetti sulla grandezza che si cerca e poi gli effetti si sommano.

Circuito equivalente di Thevenin

Si supponga di avere una rete composta di soli elementi lineari, e si consideri una generica coppia di morsetti, in modo da avere un bipolo. Si studia il bipolo tramite un generatore di corrente noto. Si utilizza il principio di sovrapposizione degli effetti e si ottiene v = R_eqi + v₀, in cui R_eq è la resistenza e quivalente della rete e v₀ è la tensione dovuta alla rete o tensione a vuoto.

Per il principio di equivalenza, la rete o il suo equivalente serie di generatore di tensione v₀ e resistore di R_eq.

E' necessario disporre di un metodo per identificare R_eq e v.

1) Si risolve direttamante la rete (si ottiene una v in funzione di i ed e, i cui coefficienti son la resistenza e la tensione a vuoto);

2) Si valutano la resistenza equivalente e la tensione a vuoto, che sono rispettivamente la resistenza che si incontra entrando da un morsetto ed uscendo dall'altro e la tensione fra gli stessi;

3) Si usa la tensione a vuoto e la corrente di cortocircuito, ovvero si calcola la R_eq e poi si cortocircuita la rete e si trova la i passante per il c.c., si utilizza successivamente la formula v₀ = -R_eqi₀.

Circuito equivalente Norton

O circuito equivalente parallelo. Si tratta di valutare il circuito preceente con un generatore di tensione noto. Tutto il procedimento è simile, eccezion fatta che in luogo di v₀ si ha i₀, corrente di cortocircuito.

Dato un circuito equivalente Norton, è possibile passare all'equivalente Thevenin o viceversa, secondo lo schema:

- T : R_eq, v₀ N : R_eq, i = (v₀ / R_eq);

- N : R_eq, i₀ T : R_eq, v₀ = R_eqi₀.

Non tutti i circuiti hanno entrambe le rappresentazioni.

Analisi di una rete con un resistore non lineare

1) Si tolga il resistore non lineare: si ottiene un bipolo lineare. Si calcoli un suo equivalente, di Norton o di Thevenin;

2) Si rappresenti la rete tramite il suo circuito equivalente che si osserva ai morsetti tolto il resistore non lineare;

3) Si risolva graficamente. Solitamente non esiste un metodo analitico: va usato un metodo di calcolo numerico. Uno dei più usati è quello di Newton, in cui nell'equazione si itera il risultato dato da un valore di partenza, sino a che il risultato, per infinite prove, converge. Non è detto che ogni valore di parenza il risultato converga. Il metodo grafico aiuta la scelta del valore iniziale. La soluzione grafica si ottiene inserendo in un grafico iXv la rappresentazione di v₀ e della v incognita.

Circuito equivalente per il piccolo segnale

Si hanno due generatori: v_b e v_s. Si dice generatore di polarizzazione il generatore v_b, mentre v_s è il generatore di segnale. Perchè si abbia un piccolo segnale, è necessario che .

Solitamente il generatore segnale è di tipo trigonometrico. La soluzione della rete si sposta in un intorno di (i_q, v_q), la soluzione del circuito in assenza di generatore di segnale. La soluzione varia su una piccola parte della caratteristica del circuito.

Se nel circuito è presente un resistore non lineare governato da v = h(i), lo approssimo come v = h(i_q) + h'(i_q(i - i_q) ovvero il resistore non lineare viene sostituito dalla retta tangente al suo grafico nel punto soluzione della rete. v = v_q + h'(i_q)(i - i_q), cioè è possibile dire v = v_q + r_q(i - i_q) in cui r_q = h'(i_q) è detta resistenza differenziale.

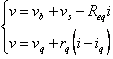
Si può ulteriormente semplificare ritenendo interessanti le variazioni di i e v, cioè di_q e dv_q, su un nuovo piano di riferimento.

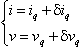
da cui

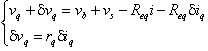
ma da v_q = v_b - R_eqi_q = h(i_q) si ha

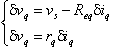
Per la soluzione risolvo il circuito con il generatore di segnale nullo, ed individuo i_q, v_q e poi r_q. Poi applico il sistema trovato.

Generatori di armoniche

Nelle reti resistive lineari non si ha distorsione: se si applica un'onda sinusoidale la si ritrova ovunque con la stessa frequenza. Nelle reti non lineari la situazione cambia, pur essendo la dipendenza istantanea e non avendo le reti memoria, si ha distorsione. Gli elementi non lineari generano armoniche di segnali.

Un esempio è se il segnale non è un piccolo segnale: è necessario migliorare l'approssimazione del dispositivo:

Reti con resistori lineari a tratti

Per la soluzione di questi circuiti non si considerano le condizioni di validità delle caratteristiche. Si risolvono tutti i circuiti possibili, in base ai rami diversi delle caratteristiche. Trovate delle soluzioni, queste si confrontano con le condizioni di validità delle caratteristiche. In questo modo si risolvono anche reti con più resistori non lineari.

Esistono sempre delle soluzioni? Se esistono, quante sono?

Nel caso di resistori lineari si hanno tre casi: una soluzione, nessuna soluzione o infinite soluzioni. Nel caso di resistori non lineari ho i casi di nessuna soluzione, una soluzione o un numero di soluzioni pari al numero dei resistori o dei rami delle caratteristiche.

Teorema

La soluzione di una rete di diodi ideali, generatori ideali ed elementi lineari passivi, se esiste, è unica.

Reti con generatori pilotati

Anche queste reti si possono risolvere applicando le tecniche sopra esposte, seguendo la procedura:

1) Si assumano noti tutti i generatori, ivi compresi i pilotati. Si valutino le grandezze pilota e le grandezze interessanti: esse verrano in funzione di a e di ê.

2) Si risolvano le grandezze pilota;

3) Ora che i pilotati sono realmente noti si risolve la rete o le grandezze interessanti.

Calcolo di un generatore equivalente di un bipolo con generatore pilotato

Nel caso in cui le grandezze pilota siano esterne al bipolo, questo equivalente non dà problemi. nel caso in cui le grandezze pilota fossero interne è necessario prestare la massima attenzione. E' possibile arrivare all'equivalente in tre modi distinti:

- Via diretta, la cui unica incertezza è nell'esistenza o meno dell'equivalente cercato;

- valutazione di v₀ e R_eq: è facile fare dei pasticci, in quanto se si annullano tutti i generatori e si valuta R_eq non si tiene conto del fatto che i generatori dipendono dai rami che si sono scelti per valutare R_eq, e quindi è come se si avesse un generatore esterno che muta le grandezze pilota e così per v₀ si possono ottenere dei valori "strani";

- Valutazione di v₀ e i₀: è solitamente una scelta ottima, ma è possibile che R_eq sia indefinita.