SCARICA DI UN CONDENSATORE

Scrivere la parola Seleziona una categoria selezionaarte biologia chimica diritto economia elettronica fisica geografia informatica inglese italiano latino letteratura lingue management marketingmatematica psicologia ricerche sociologia storia storia dell arte tecnica tecnologia meccanica tedesco varie

  SCARICA DI UN CONDENSATORE

PREMESSA

Un conduttore isolato nello spazio e lontano da altri corpi elettrizzati, avente carica Q, è soggetto all'azione del campo elettrico da esso creato e quindi ha un potenziale V=0.

Aumentando Q aumenta anche V : si verifica che esiste una diretta proporzionalità tra V e Q , ovvero che Q/V = C  cost

Un condensatore  è un dispositivo costituito da due conduttori affacciati, detti armature, disposti in modo tale da avere una elevata capacità. Il condensatore piano in particolare, è costituito due lamine metalliche piane di area S, poste, parallele, a distanza d l'una dall'altra ( con S>>d); tra esse può esservi il vuoto oppure un dielettrico.

Caricando una armatura a +Q e ponendo l'altra armatura a terra, su quest'ultima viene indotta una carica -Q. Il campo elettrico che si crea tra le armature del condensatore piano è uniforme.

Indicando con V₂ e V₁ i potenziali elettrici assunti dalle due armature 

quando posseggono cariche +Q e -Q, si ha che la DIFFERENZA DI POTENZIALE tra le armature

è proporzionale a Q : Q = C (V₂ - V₁)

In tal modo la capacità del condensatore è C = Q/V

l  PROCESSO SI SCARICA

Consideriamo un circuito in condizioni quasi stazionarie, ovvero lentamente variabili nel tempo. Istante per istante si può pensare il circuito in equilibrio, naturalmente con valori istantanei delle grandezze in gioco.

Nel caso della scarica (carica) di un condensatore piano C attraverso una resistenza R si ha un circuito in condizioni quasi stazionarie.

Se in un determinato istante e dopo aver fatto caricare il condensatore (in parte o totalmente) si esclude il generatore, questo inizierà a perdere la carica posseduta che sarà dissipata nella resistenza.

Nell'istante generico t la differenza di potenziale V_C ai capi del condensatore è uguale a quella V_R ai capi della resistenza quindi valgono le relazioni:

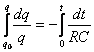
e passando ad integrare:

Risolvendo quest'ultimo integrale ottiene:

In fase di scarica conviene misurare la tensione ai capi del condensatore:

Infatti è possibile cambiando variabili linearizzare la curva rappresentandola in scala semilogaritmica (t,V_C) poiché:

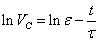
Dalle relazioni appena esposte si evince che la carica e la differenza di potenziale decrescono esponenzialmente nel tempo con una rapidità caratterizzata dalla costante di tempo t = RC, la quale ha le dimensioni di un tempo e caratterizza la rapidità di scarica.

[RC= il tempo che impiega il condensatore per raggiungere il 36% di carica rispetto alla carica iniziale. Più Rc è grande e più capiente è il condensatore]

i

f/RC

(R+r)C

Lo scopo dell'esperimento è quello di verificare la scarica di un condensatore di capacità C attraverso una resistenza R collegata in serie. Verificare inoltre che i dati ottenuti sperimentalmente coincidano con i dati teorici.

Il materiale utilizzato durante l'esperienza è il seguente:

generatore di tensione continua

condensatore elettrolitico di capacità 1000 μF

resistenza R=55,5 kΩ

voltmetro

contasecondi

ESECUZIONE

Si procede montando il circuito

+
+ C R

- -

N.B.: il condensatore elettrolitico è polarizzato, quindi bisogna stare attenti al verso della corrente.

PROCESSO DI SCARICA

Si può verificare il processo di scarica caricando C dopodichè si chiude il circuito e si rilevano le tensioni ad intervalli regolari di tempo(10 secondi).

Raccogliamo quindi i dati in una tabella .

N.B.: nell'esperienza è stato utilizzato un condensatore con capacità elevate, di modo da osservare con più facilità la sua scarica.

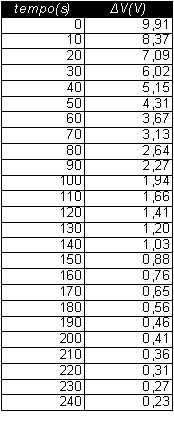
Costruiamo quindi un grafico nella quale si evidenzia l'andamento decrescente di V: il valore limite di V e quello della tensione di alimentazione V₀.

con t = RC

Ricaviamo poi V(t) teoricamente e mettiamo le due tabelle ottenute a confronto verificando così l'esattezza dei dati sperimentali (grafico n°1)

Utilizzando la tabella dei codici colore delle resistenze calcoliamo la restistenza del resistore

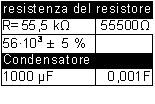
ore

Criteri per la lettura delle strisce colorate per i 'codici' a 4 ed a 5 colori.

Calcolatore per il codice dei colori dei resistori

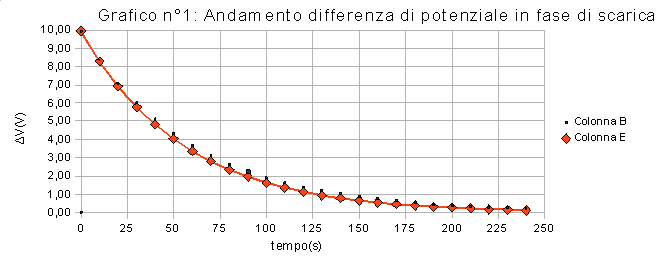
Colonna B rappresenta l'andamento sperimentale mentre colonna E rappresenta l'andamento teorico del condensatore in fase di scarica.(n.B: che le due curve coincidono quasi completamente, l'errore è dovuto all'errore sperimentale)

Dopodichè elaboro un'altro grafico utilizzando la scala logaritmica verificando così l'andamento esponenziale del condensatore, cioè significa che il condensatore di scarica con andamento esponenziale.(grafico n°3)

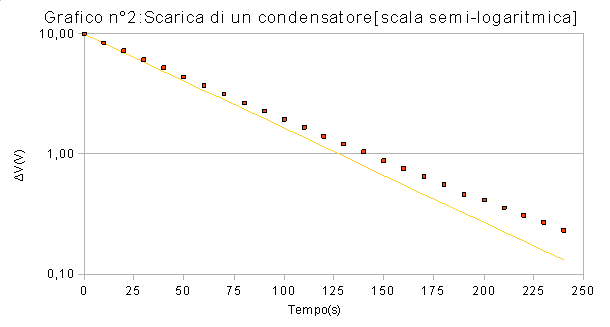
Dopodichè si calcola il logaritmo naturale in base i di ΔV e si riportano i dati in una tabella

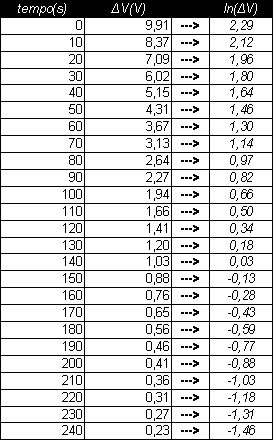
Andiamo così a ricavare il rispettivo grafico utilizzando i dati ottenuti e verifichiamo così la pendenza della retta(grafico n°3). 

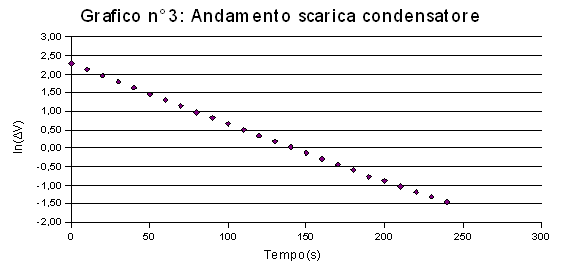
Dati ottenuti sperimentalmente calcolando la pendenza del grafico n°3

K=-0,02 1/ΩF 2,25

in cui 0,02 rappresenta la m della retta y=mx+q; mentre 2,25 rappresenta la q.

Ora calcolo teoricamente  la pendenza della retta utilizzando la segunete formula

-l/RC

·0,001 F)=0,02 ΩF

Mettendo a confronto i due dati ottenuti, quello sperimentale e quello teorico, posso verificare che i due dati coincidono e che quindi -l/RC coincide con il coefficente angolare della retta con asceisse il tempo(t) e per ordinate il logaritmo naturale di ΔV.