STATICA DEI FLUIDI

PRESSIONE    

I corpi si presentano allo stato solido, liquido e gassoso. I solidi hanno una forma e un volume proprio, i liquidi un volume proprio e la forma del recipiente che li contiene, i gas non hanno né volume né forma propria, ma tendono ad occupare tutto lo spazio, messo a loro disposizione.

Per applicare una forza ad un corpo solido rigido, possiamo applicarla ad un suo punto qualsiasi. Ciò non si può fare con un liquido. Provate a spingere con la mano la superficie libera dell'acqua. Essa affonderà semplicemente nel liquido. Per avere degli effetti la forza deve essere applicata ad uno stantuffo, che è una superficie rigida , a contatto con la superficie libera del liquido,e che può liberamente scorrere all'interno del recipiente, senza però far fuoriuscire del liquido. Gli effetti dipenderanno sia dalla forza sia dalla superficie e cioè da una nuova grandezza che dipende dalla forza e dalla superficie. Per capire qual è questa nuova grandezza si prendano due recipienti, muniti di stantuffo, riempiti di liquido che può liberamente passare da un recipiente all'altro.

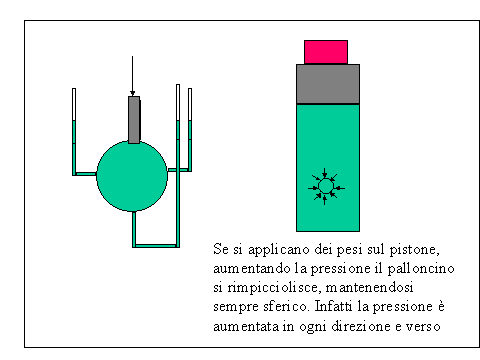
Se agli stantuffi non è applicata nessuna forza essi restano in equilibrio. Se applichiamo una forza parallela ad una delle superficie degli stantuffi l'equilibrio non è modificato(la forza parallela alla superficie non produce nessun effetto all'interno del liquido) . Se invece applichiamo una forza perpendicolare alla superficie del pistone a sinistra, quello a destra si solleva. Per riottenere l'equilibrio dobbiamo applicare una forza perpendicolare alla superficie dello stantuffo di destra. Tale forza però deve essere più grande in quanto la superficie su cui si distribuisce è maggiore. All'equilibrio si avrà sempre F₁/S₁=F₂/S₂ dove F₁ è la forza che agisce perpendicolarmente sulla superficie S₁ e F₂ è la forza che agisce perpendicolarmente sulla superficie S₂. Gli effetti dipendono perciò da una nuova grandezza, che chiamiamo pressione che è eguale a F/S: la sua unità di misura è nel SI N/m² e nel sistema pratico kg_p/m². 1 N/m² = 9,806 kg_p/m². Alla pressione contribuisce solo la componente della forza, applicata al pistone, perpendicolare alla superficie del pistone. La pressione è una grandezza scalare, essa infatti non ha una direzione, ma si esplica all'interno del liquido in ogni direzione e verso( Principio di Pascal). Infatti l'effetto della forza che agisce ad esempio sul pistone di sinistra verso il basso, ha conseguenza anche sulle pareti laterali del cilindro di destra e se vi fosse in quella posizione uno stantuffo esso si sposterebbe. Infatti quando un liquido si trova a contatto con una superficie rigida la sua pressione dà luogo ad una forza perpendicolare alla superficie ed eguale a p*S.

Un'ulteriore esperienza che dimostra il fatto che la pressione si esplica in ogni direzione e verso è la seguente. Nella ura un liquido è contenuto nel recipiente che ha diversi fori in diverse direzioni e posizioni. Se premiamo sul pistone verso il basso, il liquido si innalzerà nello stesso modo in ogni ramo indipendentemente dalla posizione e direzione del ramo stesso Ciò avviene proprio perché la pressione si esplica in ogni direzione e verso.

PRESSIONE IDROSTATICA.

All'interno di un liquido esiste una pressione, dovuta allo stesso liquido e più precisamente al peso del liquido che sta sopra al punto considerato. Perciò , quando ci si immerge, ci sentiamo sempre più compressi, man mano che scendiamo sotto il livello del mare. Tale pressione prende il nome di pressione idrostatica. Essa aumenta all'aumentare dell'altezza (profondità) e dipende dal tipo di liquido considerato. Prendiamo infarti un tubo ad U che riempiamo di liquido. Questo raggiungerà nei due rami lo stesso livello in quanto sulle sue superficie libere agisce la stessa pressione.

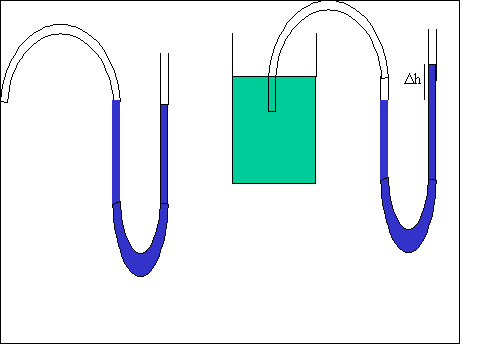
Se aumentiamo la pressione in uno dei due rami si creerà fra gli stessi un dislivello tanto maggiore quanto maggiore sarà l'aumento di pressione nel ramo che si abbassa.

Se con un tubo di gomma colleghiamo uno dei due rami e la sua estremità la immergiamo in un recipiente pieno di liquido il livello di liquido nel tubo ad U si abbasserà nel ramo collegato  al tubo e il dislivello aumenterà all'aumentare della profondità. La pressione all'interno del liquido cresce all'aumentare dell'altezza. Se nel recipiente mettiamo un liquido diverso(di diversa densità) il dislivello sarà diverso a parità di altezza. La pressione dipende anche dalla natura del liquido

Alcune notazioni:

La densità è la massa per unità di volume ed è eguale al rapporto m/V.

Il peso specifico è il peso per unità di volume ed è eguale P/V.

Il peso come sappiamo è la forza di gravità che nel sistema internazionale si misura in N. Se indichiamo con g una costante che vale 9,806m/s² e sappiamo la massa in Kg per sapere il peso in N possiamo moltiplicare m*g. P_S= peso specifico.

P_S= P/V= m*g/V=d*g; P=p_S*V=d*g*V

Si è detto che la pressione di un liquido è dovuta al fatto che al disopra del punto considerato insiste una certa quantità di liquido che ha un certo peso. Consideriamo un punto all'interno del liquido che si trovi ad una certa profondità h, distanza dalla superficie libera del liquido. Immaginiamo di tracciare a questo livello una superficie rigida ideale.

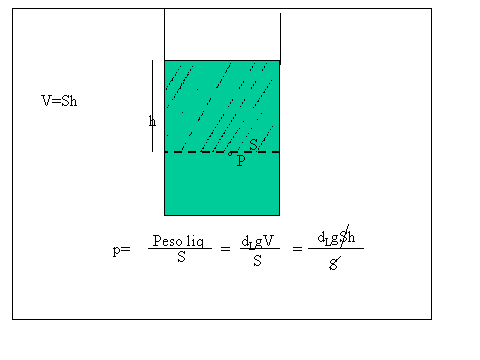
Su tale superficie agirà il peso del liquido che è perpendicolare alla superficie e che dà luogo ad una pressione che per definizione è F/S dove F è il peso del liquido che sta al di sopra della superficie considerata e che è compreso nel volume tratteggiato della ura. Il peso di tale liquido si può calcolare moltiplicando il peso specifico del liquido per il volume che è pari a S*h. P=p_SL*S*h= d_L*g*S*h; p=P/S= d_L*g*S*h/S= d_L*g*h.

Dal fatto, che la pressione idrostatica dipende dall'altezza e dal liquido, discende una particolare unità di misura di pressione che è il mm di Hg, detto anche tor. La pressione di 1 tor è equivalente alla pressione esercitata da una colonnina di mercurio alta 1 mm. Per passare dai mm hg ai pascal (N/m²) bisogna passare dai mm ai m e moltiplicare per la densità del mercurio e per g=9,806m/s², applicare cioè la formula della pressione idrostatica( il mercurio è un liquido).

d_hg=13600Kg/m³; 1tor=13600Kg/m³* 9,806m/s²*10^-3m=133,36 pascal.

PRINCIPIO DEI VASI COMUNICANTI.

Una delle conseguenze del fatto che la pressione di un liquido dipende dall'altezza e dalla natura del liquido(densità) è il principio dei vasi comunicanti. Se immettiamo lo stesso liquido in recipienti diversi, ma in comunicazione fra di loro, il livello raggiunto dal liquido nei vari recipienti, indipendentemente dalla loro forma e dal loro volume , è eguale e, se è diverso, il liquido fluirà dal recipiente a livello maggiore negli altri fino a quando non avrà raggiunto lo stesso livello in tutti i recipienti. Se prendiamo infatti una superficie che si trovi al livello più basso, per l'equilibrio su di essa deve agire la stessa pressione. Essendo i liquidi eguali,avranno pari densità e la pressione sarà identica se le altezze sono eguali. La rete idrica è un insieme di vasi comunicanti, costituito dalle utenze( i rubinetti delle varie case) e la sorgente o serbatoio. Per poter raggiungere tutte le utenze la sorgente o il serbatoio deve avere un livello più alto di tutte le utenze. Se un'utenza si trova ad un livello maggiore non sarà raggiunta dall'acqua, ameno che non si usi una pompa.

Se in due recipienti comunicanti mettiamo due liquidi di densità diversa e non miscibili, il livello sarà diverso e sarà maggiore per il liquido meno denso, le altezze saranno inversamente proporzionali alle densità.

S è la superficie di separazione dei due liquidi e S' è la superficie che si trova allo stesso livello nell'altro ramo. Per l'equilibrio su queste superficie deve agire la stessa pressione d'*g*h'=d*g*h d'/d=h/h'.

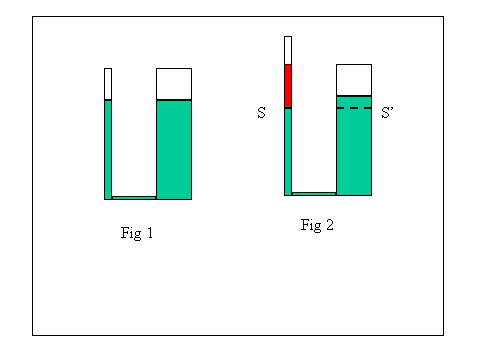
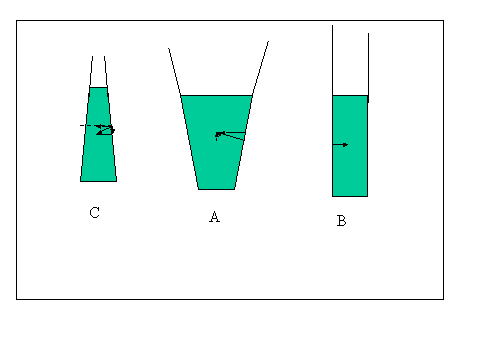Paradosso idrostatico

Siano A B e C tre recipienti con la stessa base e riempiti di liquido allo stesso livello. Le forze che agiranno sulle tre basi è p*S ed essendo la pressione eguale e la superficie eguale anche le forze saranno eguali, pur essendo il peso del liquido immesso nei tre recipienti diverso P_A>P_B>P_C: Per calcolare le forze che agiscono sulle basi bisogna tener conto anche delle reazioni vincolari delle pareti laterali: Infatti la pressione che agisce sulle pareti laterali dà luogo ad una forza perpendicolare alla parete che reagisce con una forza eguale e contraria. Nel caso di A tale reazione avrà una componente perpendicolare alla base con verso diretto verso l'alto, perciò F_A= P_A-R_N, per B la reazione è parallela alla parete perciò F_B= P_B ,per C la reazione avrà una componente perpendicolare alla base diretta verso il basso perciò F_C= P_C+R_N. Per questo F_A= F_B= F_C=p*S.

  SPINTA DI ARCHIMEDE.

Fissiamo ad un dinamometro un corpo. Il dinamometro si allungherà sotto l'effetto della forza peso del corpo. Il dinamometro misurerà quindi il peso del corpo. Facciamo la stessa cosa con il corpo immerso in un liquido. Si noterà che il dinamometro segnerà una forza minore. Siccome la forza di attrazione che agisce sul corpo è rimasta identica sul corpo immerso nel liquido agisce una nuova forza che deve avere verso opposto rispetto al peso. Nel primo caso sulla molla agisce solo P, nel secondo agisce P e una forza diretta verso l'alto, che chiameremo spinta di Archimede, in modo che la forza misurata è la somma algebrica di queste due forze.

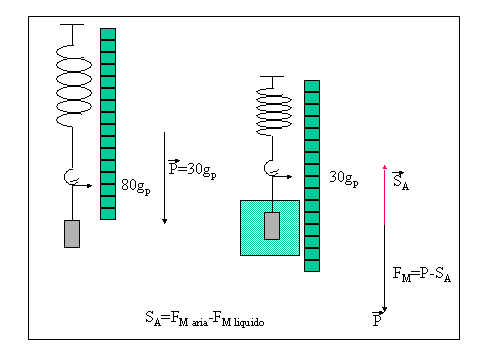
F_1mis= P   F_2mis=P-S_A ; da cui S_A= F_1mis- F_2mis.

I corpi immersi in un liquido ricevono una spinta che va dal basso verso l'alto. Per vedere a chi è eguale tale spinta si fa il seguente semplice esperimento.

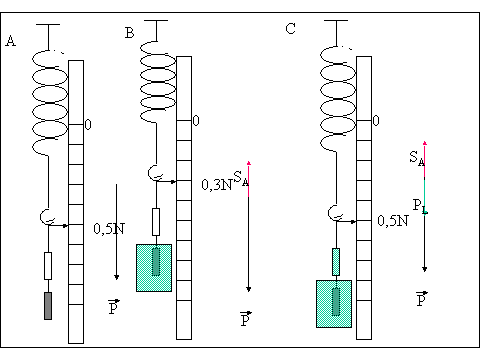
Si prendono due corpi uno cavo e uno pieno in modo che il pieno entri perfettamente nel cavo. Il volume della cavità è esattamente eguale al volume del corpo pieno. Si appendono entrambi ad un dinamometro il pieno sotto (caso A). Il dinamometro misurerà il peso dei corpi. Si immerge il corpo pieno in un liquido (caso B), il dinamometro ci darà una misura minore in quanto misura il peso e la spinta di Archimede. Si riempie il corpo cavo dello stesso liquido in cui è immerso il corpo pieno (caso C). Il dinamometro misura il peso dei corpi la spinta di Archimede e il peso del liquido contenuto nella cavità. Qualunque siano i corpi e qualsiasi liquido usiamo, si avrà sempre F_A=F_C. F_A=P; F_C=P+P_L-S_A ; S_A=P_L. La spinta di Archimede è eguale al peso del liquido che c'è nella cavità, il cui volume è eguale al volume del corpo immerso e cioè al volume di liquido spostato. Possiamo perciò dire che (Legge di Archimede):

UN CORPO IMMERSO IN UN LIQUIDO RICEVE UNA SPINTA CHE VA DAL BASSO VERSO L'ALTO ED è PARI AL PESO DEL VOLUME DI LI LIQUIDO SPOSTATO. S_A=d_L*g*V_{C imm.} V_{C imm}=V_{L Spost..}

La spinta di Archimede è una conseguenza diretta della pressione idrostatica. Infatti sulle superficie dei corpi immersi la pressione del liquido dà luogo a delle forze perpendicolari alle superficie eguali a p*S. Sulla superficie inferiore del corpo la pressione dà luogo ad una forza verso l'alto e sulla superficie superiore ad una forza verso il basso. Siccome la pressione dipende dalla profondità la forza verso l'alto è maggiore della forza verso il basso. La differenza aritmetica fra i due valori assoluti è la spinta di Archimede. Se la pressione fosse stata eguale la spinta sarebbe nulla.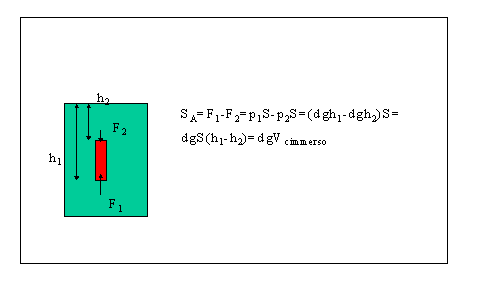

Quando un corpo è immerso in un liquido dobbiamo considerare che su di esso agiscono due forze : il suo peso che lo spinge verso il basso e la spinta di Archimede che lo spinge verso l'alto. Se P>S_A il corpo affonda, se P= S_A , il corpo è in equilibrio, resta nella posizione in cui lo lasciamo, se P< S_A il corpo va verso l'alto, affiora.

Poiché P=d_C*g*V_C e S_A= d_L*g*S*V_{c ,} se d_c>d_L sarà P>S_A e il corpo affonda, se d_c=d_L sarà P=S_A il corpo resta dov'è, se d_c<d_L sarà P<S_A e il corpo galleggia. Se d_c<d_L rl corpo affiora e una parte del suo volume resta immersa. Se V_c è il volume di tutto il corpo e indichiamo con V_{c imm} la parte di volume che è sotto il pelo del liquido dovrà essere S_A= P e cioè d_L*g*V_{c imm}= d_c*g*V_c. Da questa eguaglianza ci possiamo calcolare la parte immersa V_{c imm}= V_c*d_c/d_L. Se conosciamo la densità del corpo possiamo calcolarci, misurando la parte immersa, la densità del liquido. Questo è il principio di funzionamento del densimetro che è uno strumento per misurare la densità dei liquidi.

Calcolo della densità tramite la spinta di Archimede.

Densità di un corpo solido.

Si pesa il corpo in aria e poi in acqua distillata.

P_aria=d_c*g*V_c; P_aria-P_acqua=d_acqua*g*V_c

P_aria P_aria-P_acqua )= d_c*g*V_c/ d_acqua*g*V_c ;

d_c= P_aria P_aria-P_acqua )*d_acqua

Densità di un liquido.

Si pesa un corpo qualsiasi in aria in acqua distillata e nel liquido di cui si vuol determinare la densità.

S_A(acqua) = P_aria-P_acqua = d_acqua*g*V_c

S_A(liquido) = P_aria-P_liquido = d_L*g*V_c

(P_aria-P_liquido )/ (P_aria-P_acqua) = d_liquido*g*V_c/ d_acqua*g*V_c

d_liquido= (P_aria-P_liquido )/ (P_aria-P_acqua)*d_acqua

La determinazione della densità con questo metodo è molto precisa, in quanto non viene misurato il volume,la cui misura comporta grandi imprecisioni