Calcolo Combinatorio

Calcolo Combinatorio

			semplici

Combinazioni

Disposizioni

			Con ripetizione
	con ripetizione

[Conta l'ordine] [L'ordine non conta]

Disposizioni semplici

Def: Dati n elementi distinti, si chiama disposizione semplice degli n elementi presi k a k, con k ≤ n, un gruppo ordinato formato da k degli n   elementi dati.

N.B. Nelle disposizioni semplici non ci sono ripetizioni, pertanto due disposizioni differiscono sia quando hanno elementi diversi, sia quando hanno gli stessi elementi me è diverso l'ordine.

Teo: Il numero delle disposizioni semplici di n elementi di classe k è dato da:

Ovvero è il prodotto di k numeri consecutivi decrescenti a partire da n.

Ex: Ad un concorso con 4 posti partecipano 12 concorrenti. Quante solo le possibili graduatorie di vincitori?  .

Permutazioni semplici

Def: Si chiama permutazione semplice di n elementi una disposizione semplice di n elementi presi ad n a n:

(fattoriale).

Ex: In quanti modi 4 giocatori si possono disporre attorno ad un tavolo quadrato?  

Disposizioni con ripetizione

Def: Dati n elementi distinti si dice disposizione con ripetizione degli n elementi presi a k a k, con k intero qualunque, un gruppo ordinato di k elementi in cui ogni elemento può essere ripetuto fino a k volte.

Teo:

Ex: In quanti modi si può rispondere ad un test di V/F di 12 domande? .

Combinazioni semplici

Def: Dati n elementi distinti, si chiama combinazione semplice degli n elementi di classe k con k ≤ n ogni sottoinsieme formato da k elementi.

N.B. Dato I = la combinazione di classe k, sono tutti i sottoinsiemi di I di cardinalità k (con  elementi).

In generale, le combinazioni sono: .

Teo:

Oss: Le combinazioni di n elementi di classe k si indicano con il simbolo chiamato coefficiente binomiale. Pertanto: 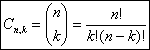proprietà dei tre fattoriali

Ex: Quante sono le combinazioni possibili per fare 6 al superenalotto?

Proprietà del Coefficiente binomiale

Richiami:

Rappresenta il numero di sottoinsiemi di cardinalità k di un insieme di n elementi.

Proprietà:

=> l'insieme vuoto

=> ogni sottoinsieme ha un solo sottoinsieme vuoto

=

proprietà delle classi complementari (ogni sottoinsieme di cardinalità ne individua un altro di cardinalità n-k).

formula di Stifel EX:

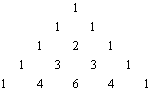Binomio di Newton

(a + b)⁰ = 1

(a + b)¹ = a + b

(a + b)² = a² + 2ab + b^{2 TRIANGOLO DI TARTAGLIA}

(a + b)³ = a³ + 3a²b + 3ab² + b³