| matematica |
|
|||||
|
LOGARITMI
Logaritmo: y = log![]() x | x
x | x ![]() a à
a à
Il logaritmo di un numero è l’esponente che bisogna dare alla base per ottenere quel numero.
Definizioni:
log![]() 1 = 0 4. log
1 = 0 4. log![]() 7. log
7. log![]()
log![]() a
= 1 à log
a
= 1 à log![]() a
a![]() = n 5. log
= n 5. log![]()
log![]() x
= n 6. log
x
= n 6. log![]()
Proprietà:
Il logaritmo in una data base del prodotto di 2 o più numeri è uguale alla somma dei logaritmi di ciascun
numero in quella base .
log![]() m* n = log
m* n = log![]() m
+ log
m
+ log![]() n
n
Il logaritmo in una data base del quoziente di 2 numeri è uguale alla differenza tra i logaritmi del
dividendo e del divisore in quella base.
log![]()
![]() = log
= log![]() m
+ log
m
+ log![]() n
n
3. Il logaritmo in una dat base di una potenza è uguale al prodotto tra l’esponente di quella potenza ed il
logaritmo della base della potenza.
log![]() m
m![]() = n* log
= n* log![]() m
m
Tipi di scrittura nella notazione italiana:
Logaritmo decimale: Log
Logaritmo neperiano: log (e = 2,73) = logaritmo naturale = ln
Funzione logaritmica:
y
= log![]() x
x
Distinguiamo 2 casi:
1. se a > 1: FUNZIONE CRESCENTE 2. SE 0 < a <1 : FUNZIONE DECRESCENTE
![]()
![]()
![]()
![]() y = a
y = a![]() y
y
![]()
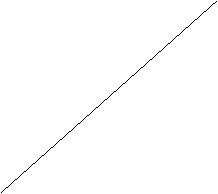



 y y =
y y = ![]() y = log
y = log![]() x
x
 y = log
y = log![]() x
x
1
![]()
![]()
![]()
![]()
![]() 0 1 x 0 1 x
0 1 x 0 1 x
![]()
![]()
Bisett. I e III q. bisett. I e III q.
D = C = D = C =
log![]() f(x)
> log
f(x)
> log![]() f(x)
f(x)
Esempi:
D =
x![]() +
x – 6 > 0 (x –
2) (x + 3) > 0 x > 2 U x < -3
+
x – 6 > 0 (x –
2) (x + 3) > 0 x > 2 U x < -3
x – 2 > 0 x > 2 x > 2
x + 3 > 0 x > -3 x > -3
-3 2
![]()
![]()
![]()
![]()
![]()
![]()
![]() D
=
D
=
![]()
![]()
log![]() (x
(x![]() +
x -6 ) = log
+
x -6 ) = log![]() (x
-2) ( x +3)
(x
-2) ( x +3)
log![]() (x
(x![]() +
x – 6) = log
+
x – 6) = log![]() (x + x – 6 ) à IDENTITA’ : S = x € R
(x + x – 6 ) à IDENTITA’ : S = x € R
S = D + S = x >2
C.E. =
4x + x![]() >0
>0
x (x + 4) > 0
x < -4 U x > 0
C.E. =
log![]() (4x + x ) < log
(4x + x ) < log![]()
4x + x![]()
![]()
2x![]() + 8x -l
+ 8x -l ![]() 0
0
x![]() =
=
![]()
S = x ![]()
![]() U x
U x ![]()
![]() )/2 -4 0 (-4+3
)/2 -4 0 (-4+3![]()
![]()
![]()
![]()
S = 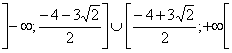
|
Privacy
|
© ePerTutti.com : tutti i diritti riservati
:::::
Condizioni Generali - Invia - Contatta