Prime nozioni di Calcolo delle Probabilità

Ogni volta che siamo di fronte ad un incertezza parliamo di probabilità che un certo evento si verifichi.

Esempi:

Prob. che domani non piova

Prob. che nella prossima estrazione del Lotto

il numero 24 esca sulla ruota di Roma

Prob. che un certo studente riesca a superare l'esame di statistica

Prob. che una certa squadra di calcio riesca a vincere lo scudetto nel 2001.

Prob, di ottenere un doppio 6 lanciando due dadi

Prob. che il tasso d'interesse bancario sia, tra 5 giorni, superiore al 4%.

Per rispondere a queste domande occorrono diverse capacità, tra cui

Nozioni di calcolo di probabilità

Esperienza nel settore specifico

In questo corso cercheremo di acquisire le nozioni elementari di cui al primo punto.

Che cosa è la probabilità?

E' un numero compreso tra 0 e 1 che viene associato ad un evento. In principio, ognuno può assegnare la propria personale probabilità a ciascun evento purché rispetti alcune elementari regole di coerenza.

Per poter parlare di probabilità di eventi dobbiamo immergerci in un contesto sperimentale.

C'è un esperimento (una prova) che può dar luogo a diversi risultati: questi risultati, gli eventi elementari, in genere hanno diverse probabilità di verificarsi.

Esempio

Si lancia un dado con sei facce su un tavolo (esperimento), e siamo interessati alla faccia superiore (non, ad esempio, ai centimetri percorsi dal dado sul tavolo). I sei possibili risultati (eventi elementari) sono

Vedremo più avanti che la probabilità dell'evento

sarà pari a 1/6.

E' importante qui notare, ad esempio, che gli eventi

non avrà la stessa probabilità dell'evento .

Che cosa è un evento?

Un qualsiasi fatto o proposizione che non sappiamo essere vero o falso e perciò quantifichiamo la nostra fiducia sul suo essere vero attraverso un numero compreso tra 0 e 1.

Esistono diversi modi di definire la probabilità

Definizione classica

Prob = # casi favorevoli / # casi possibili

(troppo restrittiva, vale solo in circostanze particolari)

Definizione frequentista

Se un evento E è relativo ad una certa prova, ipoteticamente ripetibile un gran numero di volte

P= lim_{n ¥} Freq. Rel (E)

(più generale, ma non applicabile ad eventi non ripetibili, come ad esempio una partita di calcio)

Definizione soggettiva

La probabilità di un evento è il grado di fiducia che abbiamo nella sua realizzazione. In altri termini P è il prezzo p (compreso in [0,1]) che riteniamo giusto are per partecipare ad una scommessa in cui si vince 1 se l'evento si verifica e 0 se non si verifica

(dovuta a de Finetti (1921), del tutto generale ma che permette alla probabilità di essere diversa da individuo  a individuo)

Esempio:

Consideriamo un'urna con b palline bianche, e n palline nere.

Si estrae una pallina. Calcolare P.

In questo caso le b+n palline, per ragioni di simmetria hanno tutte la stessa probabilità di essere estratte e possiamo usare la definizione classica per cui P=b/(b+n).

Attenzione: se b¹n, P¹

Se si estraggono 2 palline qual è la probabilità di estrarne 2 bianche?

Dipende dal tipo di estrazione:

Si possono estrarre palline da un urna

Con ripetizione (reinserendo la pallina nell'urna)

Ad ogni estrazione l'urna ha la stessa composizione

Senza ripetizione (non reinserendo la pallina)

Ad ogni estrazione si modifica la composizione dell'urna

Lo schema di estrazione dell'urna serve da paradigma per molti esperimenti.

Esempi

Lancio di un dado

Estrazione di una carta da un mazzo

Roulette

etc .

Gli eventi come insiemi

Dal punto di vista matematico è utile trattare gli eventi come fossero sottoinsiemi di un insieme W che rappresenta lo spazio campionario, ovvero lo spazio di tutti i possibili risultati di un esperimento.

In questo modo possiamo effettuare delle operazioni logiche sugli eventi

Unione: L'evento AÈ B rappresenta l'evento che è vero quando si verifica almeno uno dei due eventi A o B.

Intersezione: L'evento A B rappresenta l'evento che è vero quando si verificano entrambi gli eventi A e B.

Negazione: L'evento (oppure) rappresenta la negazione di A e si verifica se e solo se non si verifica A. Si può scrivere anche come W-A.

Esempio: Lancio di un dado

W

Siano A= e B=.

Allora,

AÈ B =

A B

=

In questo contesto W rappresenta l'evento certo mentre la negazione di Wviene rappresentata col simbolo Æ (insieme vuoto o evento impossibile)

Di particolare importanza sono le formule di De Morgan che stabiliscono una dualità tra le operazioni di unione e intersezione e tra gli eventi e le loro negazioni.

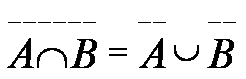
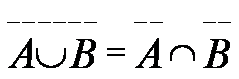
che si possono generalizzare per più di due eventi in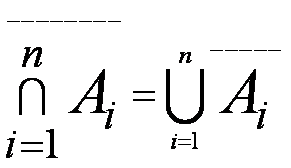

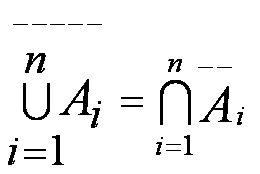
Altre operazioni sugli insiemi

Proprietà distributiva:

A (BÈ C) = (A B) È (A C)

A  È (B C) = (AÈ B) (AÈC)

Proprietà associativa:

A È (BÈ C) = (AÈ B) È C

A  (B C) = (A B) C

Esercizio: verificare le relazioni precedenti nel seguente esempio:

I possibili risultati di una estrazione del lotto sono cinquine di numeri da 1 a 90: definiamo i seguenti eventi:

A=

B=

C=

Incompatibilità tra eventi.

Due eventi A e B sono incompatibili se non possono verificarsi contemporaneamente: in simboli

A B=Æ

Altre definizioni

Due eventi si dicono necessari se almeno uno di loro deve verificarsi per forza: in simboli

AÈ B=W

Esempio: nel lancio di una moneta i due eventi T e C sono, allo stesso tempo necessari e incompatibili.

Un insieme di n eventi E₁, E₂, . , E_n , necessari e incompatibili a due a due, (cioè E_i E_j =Æ, per ogni i¹j) forma una partizione dell'insieme W

Inclusione: un insieme A si dice incluso in B, ovvero A B, se il verificarsi di A implica il verificarsi di B

Suddivisione di un unione in parti disgiunte

Dati due insiemi qualunque A e B, si può sempre scrivere

I postulati del calcolo delle probabilità

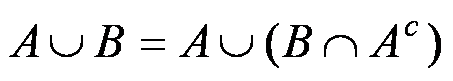
La probabilità è una funzione di insieme che associa ad ogni insieme (o evento) un numero, rispettando i seguenti postulati

P >= 0   per ogni E contenuto in W

P >= 1

Se E_i E_j =Æ, per ogni i¹j=1, . ,n,n+1, .

Allora

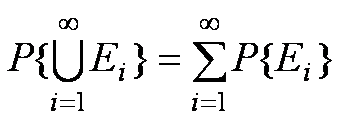
Da questi postulati è possibile dedurre una serie di teoremi che permettono di risolvere i più elementari problemi di calcolo delle probabilità.