matematica

SCHEMA RIASSUNTIVO DELLE TRASFORMAZIONI GEOMETRICHE - AFFINITA, SIMILITUDINI, OMOTETIE, ISOMETRIE

SCHEMA RIASSUNTIVO DELLE TRASFORMAZIONI GEOMETRICHE

AFFINITA'

Una trasformazione lineare si può esprimere in questo modo:

oppure

dove ( a;c ) = f ( 1;0 )

( b;d ) = f ( 0;1)

La trasformazione è individuata dalla matrice A =

con det (A) ¹ (altrimenti la matrice non sarebbe invertibile)

ricordiamo che l'inversa di una matrice è data da A^-l=

Una trasformazione lineare + una traslazione è una generica affinità che ha quindi equazione:

es.

Data la trasformazione :

1. scrivila sotto forma matriciale

2. verifica se è una affinità

3. trasforma il triangolo di vertici A(0,0) B(3,0) C(2,2)

4. trasforma la retta 2x - y = 0

5. trova la retta unita

L'affinità è una trasformazione in cui:

a rette corrispondono rette

a rette parallele corrispondono rette parallele

è costante il rapporto tra le aree di ure corrispondenti ½ad-bc½= det (A) ¹0 si dice rapporto di affinità.

riassumendo:

condizione perché una trasformazione sia un'affinità :

1. det (A) ¹

SIMILITUDINI

E' un'affinità in cui è costante il rapporto tra due qualunque segmenti corrispondenti; tale rapporto costante è chiamato raporto di similitudine

Vediamo come deve essere la matrice A; ovviamente avrà le stessa caratteristiche di un'affinità più altre.

E' una similitudine diretta se A si presenta in questa forma: det (A)= k² e ½k½= rapporto di similitudine

E' una similitudine inversa se A è del tipo: det (A)= -k² e ½k½= rapporto di similitudine

es.

forma matriciale: è . . . . . . . . ..

forma matriciale: è . . . . . . . . . ..

riassumendo:

condizioni perché una trasformazione sia una similitudine :

1. det(A)¹

2. sono uguali in valore assoluto gli elementi delle due diagonali (in una sono uguali nell'altra opposti)

se sono uguali quelli sulla diagnale principale, la similitudine è diretta ed ha det(A)>0 infatti det(A) = a²+b²

se sono uguali quelli sulla diagnale secondaria, la similitudine è inversa ed ha det(A)<0 infatti det(A) = -a² -b²

OMOTETIE

Se A= la similitudine si dirà omotetia in cui a si dice rapporto di omotetia.

il sistema sarà:

in forma matriciale :

Un'omotetia ha stesse caratteristiche dell'affinità + quelle della similitudine + gli elementi sulla diagonale secondaria nulli.

Stabilisci di quali trasformazioni si tratta analizzando le seguenti matrici:

. . . . . . . . . . . .. . . . . . .

. . . . . . . . . . . . . . . . . . . .

ISOMETRIE

(consideriamo quelle che lasciano fissa l'origine, parleremo dopo della traslazione).

Un'isometria è una similitudine con rapporto k=1; questo vuol dire:

- da un punto di vista geometrico che le dimensioni si conservano

- da un punto di vista analitico det (A) = 1 (diretta +1, inversa -1).

riassumendo

Sottolineamo che deve essere una similitudine, deve perciò avere le caratteristiche della similitudine:

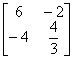1. det (A) ¹

2. sono uguali in valore assoluto gli elementi delle due diagonali (in una sono uguali nell'altra opposti)

in più:

3. det (A)

le condizioni 1, 2, 3 si riassumono dicendo che A*=A^-l dove A* è la matrice trasposta

In particolare:

isometrie dirette: rotazioni

La matrice si presenta nella forma:

con det(A)= 1

possiamo sempre scrivere la matrice A nella forma

in questo modo sappiamo l'angolo di rotazione che, come è stato dimostrato, ha ampiezza a

isometrie inverse: simmetrie assiali

La matrice si presenta nella forma:

con det(A)= -l

possiamo sempre scrivere la matrice A nella forma

in questo modo sappiamo il coefficiente angolare della retta di simmetria che, come è stato dimostrato, è

m = tan

Stabilisci di quali trasformazioni si tratta analizzando le seguenti matrici;

controlla per ciascuna matrice tutte le condizioni :

1. det (A) ¹

2. sono uguali in valore assoluto gli elementi delle due diagonali (in una sono uguali nell'altra opposti)

in più:

3. det (A)

Stabilisci inoltre, una volta concluso che si tratta di una isometria, di quale isometria si tratta:

; ; ; ; ; ; ;

Una similitudine è una composizione di una omotetia e di una isometria. Per poter riconoscere le trasformazioni elememtari che la compongono procediamo così (partiamo dall'esempio n°5)

A= det(A) = -4 Þ la similitudine è inversaÞ k²=-4 Þk=2Þ posso riscrivere la matrice in questo modo:

possiamo concludere che la similitudine in esame è la composizione di una omotetia di k=2 edi una simmetria assiale, con asse di simmetria .

Una traslazione è rappresentata da un vettore di componenti:

In generale:

ogni trasformazione affine generica:

si può pensare come la composizione di un'affinità con l'origine fissa di matrice A=

ed una traslazione di vettore v (p;q).

Per questo è sempre possibile applicare ad una trasformazione qualunque le analisi che abbiamo condotto per l'affinità con l'origine fissa, analizzando la matrice A dei coefficienti.

es.

Studiare la seguente trasformazione:

La trasformazione si può scomporre in una affinità con l'origine fissa:

ed una traslazione di vettore v (-l;2)

Studia l'affinità

Trova i punti uniti

Trova la corrispondente della retta 2x+y = 1 ( riferimento testo 569 ForMat ,Spe vol 1 )

Privacy