ESERCIZI

2.15 ESERCIZI

Nota preliminare.

In tutti gli esercizi in cui la probabilità degli eventi non è assegnata, si suppone che essa sia uniforme su W, cioè, dato un evento A, P(A)=N(A)/N, dove N(A)= numero dei casi favorevoli, N = numero dei casi possibili, o, ciò che è lo stesso N= cardinalità di W. Ad esempio per l'esperimento aleatorio E "lancio di una moneta" si ha: W= con T= e C=; P(T)=P(C)=1/2.

Esercizio N° 1

Sia l'esperimento aleatorio E "doppio lancio di una moneta". Calcolare la probabilità dell'evento "esca almeno una volta testa".

Si considerino i due spazi campioni relativi al primo ed al secondo lancio, rispettivamente W e W

W W

W W W

A==, quindi P(A)=3/4.

Si può calcolare la P(A) in modo diverso considerando i seguenti eventi:

T₁ ==; T₂ ==.

L'evento A si verifica quando si verifica almeno uno degli eventi T₁ e T₂, quindi A= T₁ T_2.

In definitiva, P(A)=P(T₁ T_2.)=P(T₁)+ P(T₂)-P(T₁ T₂ );

(T₁ T₂ )=; P(T₁ T₂ )=1/4; P(T₁)= P(T₂)=1/2, quindi P(A)=3/4.

Esercizio N° 2

Sia l'esperimento aleatorio E "triplo lancio di una moneta" e siano gli eventi:

A=; B=; C=.

Calcolare: P(A),P(B),P(C),P(A B), P(A C), P(B C), P(A B), P(A C),P(B C).

W

A=

B=

C=

A questo punto, si può fare il calcolo diretto, oppure osservare che valgono le seguenti relazioni tra gli eventi:

A B = W (infatti l'evento A B coincide con l'evento "escono zero, una o due teste"), ovvero rappresenta tutti i casi possibili.

A C=A (infatti C A);

B C=B (infatti C B);

A B=C (infatti A B==);

A C=C;

B C=C;

Si ottiene:

P(A)=7/8; P(B)=1/2; P(C)=3/8

P(A B)=P(W)=1 ; P(A C)=P(A)=7/8; P(B C)=P(B)=1/2

P(A B)=P(C)=3/8; P(A C)=P(C)=3/8; P(B C)=P(C)=3/8

Esercizio N° 3

Si supponga di comperare 300 componenti di cui 100 da un produttore A, e 200 da un produttore B; se il 40% dei componenti di A e il 30% dei componenti di B è affetto da difetti, si calcoli la probabilità che  un componente preso a caso sia senza difetto.

Introdotti gli eventi: D=; =

Con riferimento allo schema in ura,

applicando il teorema della probabilità totale, si ha:

P(D) = P(A)P(D|A) + P(B)P(D|B). Poiché:

P(A) = 1/3;   P(B) = 2/3; P(D|A) = 3/5; P(D|B)=7/10,

Sostituendo si ricava che P(D) = 2/3

Domanda: nell'ipotesi che il componente scelto risulti difettoso, quale è la probabilità che sia stato acquistato da A? e da B?

Esercizio N° 4

Con riferimento alla ura, calcolare la probabilità che alla j-ma estrazione, con j=1..6, esca una pallina bianca nel caso:

a)  che ogni  pallina estratta venga rimessa nell'urna e nel caso:

b)  che la pallina estratta non venga rimessa nell'urna. Calcolare, inoltre:

c)  la probabilità P(B) che venga estratta una pallina bianca senza sapere quante palline sono state estratte prima, ovviamente nell'ipotesi che la pallina non venga rimessa nell'urna.

Si consideri l'evento B_j=

a)  Estrazione con rimessa

È ovvio che:

P(B_j) = 4/6 = 2/3 j = 1,..,6 (in effetti, in questo caso sono possibili infinite estrazioni).

Questo risultato, come già detto, vale per ogni estrazione (fino alla 6a) anche nel caso di estrazione senza rimessa; vediamolo solo per la 2a e 3a estrazione:

b) Estrazione senza rimessa

P(B₁) = 2/3; P() = 1/3;

da cui: P(B₂) = P(B₁)P(B₂|B₁) + P()P(B₂|);

poiché P(B₂|B₁) = 3/5 e P(B₂|) = 4/5, si ottiene: P(B₂) = 2/3 e P() = 1/3.

Per calcolare P(B₃) si può applicare ancora la probabilità totale, ad esempio rispetto ai seguenti eventi che risultano essere incompatibili e esaustivi:

(B₁ B₂), (B₁ ), ( B₂), ( ).

P(B₃) = P(B₁ B₂)P(B₃ |B₁ B₂) + P(B₁ )P(B₃ | B₁ ) + P( B₂)P(B₃ | B₂) + + P( )P(B₃ | ).

Essendo:

P(B₃ |B₁ B₂) = ½; P(B₃ |B₁ ) = ¾; P(B₃ | B₂) = ¾; P(B₃ | ) = 1, si ha:

P(B₃) = 1/2 P(B₁ B₂) + 3/4 P(B₁ ) + 3/4 P( B₂) + 1 P( ); quindi

P(B₃) = 1/2 P(B₁ )P(B₂|B₁) + 3/4 P()P(B₂|) + 3/4 P(B₁ )P(|B₁) + 1 P()P(|);

poiché: P(|B₁) = 2/5; P(|) = 1/5

si ottiene: P(B₃) = 2/3 (e di conseguenza P() = 1/3)

Ripetendo il processo, si può vedere che P(B_j) = 2/3 j = 1,.., 6

c)   Caso di estrazioni senza rimessa in numero incognito

Chiamando N_k gli eventi "k-ma estrazione" e sapendo che P(B|N_k) = 2/3 j = 1,.., 6, per calcolare la P(B) (non si può scrivere B_k perché non sappiamo k quanto vale) si applica la probabilità totale condizionando rispetto agli eventi incompatibili e esaustivi:

Poiché sono eventi esaustivi, , quindi P(B) = 2/3, ancora (si noti che il risultato è indipendente dalle P(N_k), anche se sarebbe ragionevole assegnare ad esse la stessa probabilità di 1/6).

Esercizio N° 5

Un medico di fronte a un sintomo A deve individuare la malattia più probabile. Supponiamo che A, in un certo paziente, possa essere sintomo delle malattie B₁, B₂, B₃, B₄, che il medico giudica nell'ordine capaci di verificarsi con probabilità 0.4, 0.3, 0.2, 0.1. D'altra parte, l'esperienza clinica dimostra che se la malattia B₁ è presente, allora il sintomo A si verifica con probabilità P(A|B₁) = 0.4 e, similmente:

P(A|B₂) = 0.5;    P(A|B₃) = 0.6; P(A|B₄) = 0.7

Allora le probabilità a posteriori per le malattie saranno rispettivamente:

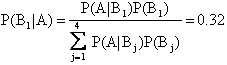
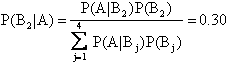
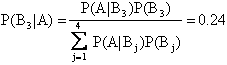
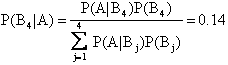
Si noti come la malattia B₁ a priori più probabile resti tale, ma la presenza del sintomo A ha modificato sostanzialmente i rapporti originari.

Esercizio N° 6

Si consideri un sistema di trasmissione digitale; per effetto del rumore, il segnale ricevuto non sempre è uguale a quello trasmesso. si supponga che la probabilità di errore sia 0.1 e cioè:

la probabilità che trasmesso 0 sia ricevuto 0 è 0.9;

la probabilità che trasmesso 0 sia ricevuto 1 è 0.1;

la probabilità che trasmesso 1 sia ricevuto 1 è 0.9;

la probabilità che trasmesso 1 sia ricevuto 0 è 0.1.

Calcolare la probabilità che sia ricevuto 0; la probabilità che sia ricevuto 1; la probabilità che sia stato trasmesso 0 dato che si sia ricevuto 0 nelle seguenti diverse ipotesi:

a) la probabilità che sia stato trasmesso 0 è 1/2;

b) la probabilità che sia stato trasmesso 0 è 0.05;

In generale, quindi, per effetto del rumore, una volta ricevuto 0, non è detto che sia stato trasmesso 0; il sistema di decodifica, allora, deve decidere se optare per uno 0 oppure per un 1, Spiegare in base a quale criterio viene effettuata tale scelta, e trovare, inoltre, un intervallo di valori di X₀ per i quali conviene optare per 0.

a)

Sia:

X₀=  P(X₀)=1/2 P(Y₀|X₀)=0.9

X₁=  P(X₁)=1/2 P(Y₁|X₀)=0.1

Y₀=    P(Y₀|X₁)=0.1

Y₁=    P(Y₁|X₁)=0.9

Poiché X₀ X₁= W e = X₁, si ha: P(Y₀) = P(X₀) P(Y₀|X₀)+P(X₁) P(Y₀|X₁). Sostituendo i valori dati, si ricava che P(Y₀)=1/2.

Procedendo in modo analogo per Y₁ si ricava: P(Y₁) = P(X₀) P(Y₁|X₀)+P(X₁) P(Y₁|X₁)=1/2.

b)

Utilizzando le stesse relazioni del caso precedente, si ottiene:

P(Y₀)=0.14;

P(Y₁)=0.86;

P(X₀|Y₀)=0.32.

Ricevuto 0, il decodificatore opterà per 0 se la probabilità che sia stato trasmesso 0 è maggiore della probabilità che sia stato trasmesso 1, cioè se P(X₀|Y₀)>P(X₁|Y₁); in altri termini, il decodificatore opterà per 0 se

;

.

Posto per comodità P(X₀)=x, il rapporto (*) risulta >1 se . La disequazione è verificata per x>0.1; quindi per 0 P(X₀) 0.1 si sceglierà il bit 0; per 0.1 P(X₀) 1 si sceglierà il bit 0.

Esercizio N° 7

Si supponga che in un reparto di una fabbrica vi siano n macchine funzionanti automaticamente. Nello stesso reparto vi è un addetto alle riparazioni, che interviene solo a guasto avvenuto. Nel caso che si guastino più macchine, l'addetto interviene sulla prima macchina che si è guastata, mentre le altre vengono messe in attesa; successivamente, interviene sulla seconda e così via fino a quando tutte le macchine vengono riparate. Se più macchine si guastano contemporaneamente, l'addetto interviene scegliendo a caso l'ordine delle macchine da riparare.

Nell'ipotesi che

la probabilità che una sola macchina si guasti è P(G1) = 0.4 ;

la probabilità che due sole macchine si guastino è P(G2) =0.2;

la probabilità che almeno tre macchine si guastino è P(G3) = 0.2;

calcolare:

a)   la probabilità che l'addetto non intervenga;

b) la probabilità che una macchina sia in attesa di riparazione dato che l'addetto sta intervenendo su di un'altra macchina.

a) L'addetto interviene quando almeno una macchina si guasta, quindi gli eventi A= coincide con l'evento .

Dire che "almeno una macchina è guasta" significa dire che se ne guasta una, o due, o più di due, quindi:    A = G₁ G₂ G₃ (1);

da cui: P(A) = P(G₁ G₂ G₃) ; essendo G₁, G₂, e G₃ incompatibili:

P(A) = P(G₁ G₂ G₃) = 0.8

La probabilità che l'addetto non intervenga è (risultato che si poteva anche calcolare direttamente).

b)   Una macchina è in attesa se se ne sono guastate almeno due; quindi l'evento B=coincide con l'evento: , cioè:

B = G₂ G₃ (2) T P(B) = P(G₂ G₃) = 0.4

La probabilità che una macchina sia in attesa dato che l'operatore sta intervenendo su di un'altra macchina è P(B|A).

Confrontando la (2) e la (1) si vede che B A T A B = B, da cui

Nota: i prossimi due esercizi, molto simili, sono un esempio di quei problemi che sono stati sbagliati anche da celebri matematici, e quindi vengono riportati anche per curiosità; il lettore che avesse difficoltà a comprendersi non deve dunque preoccuparsi. Essi tuttavia appaiono utili per capire come bisogna essere cauti nell'applicare meccanicamente le formule della probabilità (in particolare, qui si tratta della formula di Bayes).

Esercizio N° 8 ("Il paradosso dei tre carcerati")

In un carcere sono rinchiusi 3 detenuti a, b, c di cui 2 saranno giustiziati. Uno dei detenuti (supponiamo a) chiede al carceriere (d):

" Dimmi chi fra b e c verrà giustiziato.  Se, per ipotesi, ad essere giustiziati sono b e c, me ne indichi solamente uno a tuo piacimento. Ciò non cambierà il mio stato, perché già so che almeno uno di loro sarà giustiziato". Il carceriere accetta.

Dopo la risposta del carceriere il detenuto fa il seguente ragionamento:

"La probabilità di salvarmi passa da 1/3 a ½" . E' corretto il ragionamento?

Si faccia l'ipotesi che il carceriere dica sempre la verità.

Si indichi con A l'evento ; con B l'evento ; con C l'evento . La probabilità che a si salva, supposto che b venga giustiziato () é:

(*)

E' ovvio assumere: P(A) = 1/3; P() = 2/3; P(|A) = 1.

Sostituendo nella (*) si ricava P(A|)=1/2.

Il carcerato fa pressappoco il ragionamento visto, che formalmente sembra corretto, ma che tuttavia porta a risultati errati perché la risposta del carceriere è condizionata alla domanda di a; infatti la risposta che il carceriere dà ad a è condizionata al fatto che a si salvi o meno.

D'altro canto, la risposta che d dà ad a non aggiunge nulla di più di quanto a già non sapesse.

Il ragionamento corretto è il seguente:

Si considerino gli eventi = e = ; la risposta del carceriere può essere riassunta nel seguente specchietto:

Supposto che si verifichi l'evento la probabilità di salvezza di a è

(1)

P(A)=1/3; = 1/2.

P() si calcola con la probabilità totale condizionando rispetto ad A, B, C:

(2)

=1/2; = 0; = 1. Da tali valori si ricava la (2); sostituendola nella (1) si ricava = 1/3.

Dunque, come è ragionevole, la probabilità di sopravvivenza di a continua a rimanere 1/3; anzi, è la probabilità di salvezza di c che è aumentata, perché ora deve valere 2/3 (controllarlo con il calcolo), ma . . C non lo sa!.

(Nota: E' ovvio che ad un risultato analogo si giungeva supponendo che d affermasse l'evento )

Esercizio N° 9 ("il paradosso delle 3 porte")

Siano date 3 porte (a, b, c) dietro una delle quali vi è nascosto un premio. Un giocatore sceglie una porta senza aprirla, dopodiché gli viene mostrata una delle altre due porte dove non vi è il premio; se il premio non si trova dietro nessuna porta, gliene viene mostrata una a caso. A questo punto, al giocatore viene data la possibilità di confermare la porta scelta o cambiare la porta con quella delle due che non è stata aperta.

E' più conveniente confermare la porta o cambiarla?

Si supponga che il giocatore scelga la porta a. Si considerino i seguenti eventi:

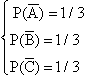
Tutti i possibili casi che si possono verificare sono:

Supposto che al giocatore venga mostrata la porta b, la probabilità che il premio si trovi dietro a è

(1)

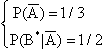
P(B^*) si ricava applicando la probabilità totale, condizionando rispetto ad :

(2)

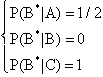  (3)

Sostituendo la (3) nella (2) si ottiene: P(B^*) = 1/2 e quindi = 1/3.

Si osservi che

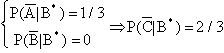
In definitiva, al giocatore conviene cambiare porta. Si può dare una spiegazione intuitiva di ciò?.

Nota: Gran parte dei matematici interpellati a proposito di questo gioco (proposto con gran successo dalla TV USA) sbagliò affermando che il calcolo delle probabilità asseriva l'equivalenza delle due scelte!