5.9 ESERCIZI

Esercizio N° 1

Si consideri il sistema al lato;

Si supponga che il generatore e le linee siano in grado di fare fronte alla massima potenza richiesta dal carico, e che siano gli unici componenti che possano guastarsi.

Con i dati affidabilistici:

P(G)=R₁=0.99; P(L₁)=R₂=0.98; P(L₂)=R₃=0.98,

a)  calcolare l'affidabilità R del sistema nell'ipotesi in cui i suoi componenti siano indipendenti.

b)  Trovare inoltre un intervallo di possibili valori di R nel caso in cui i componenti non siano indipendenti.

a) Nel caso di indipendenza si ha:

P(S) = P[G (L₁ L₂)] = P(G ) [P(L₁ ) + P(L₂) - P(L₁ )P(L₂)] = (0.99)(0.9996) = 0.9896.

b) Se gli eventi non sono indipendenti, e non si conosce la loro probabilità congiunta, si possono calcolare un limite inferiore e uno superiore per R, come segue:

poiché: P(A B) min, detti A e B i due sottosistemi in serie, si vede subito che R deve essere più piccola dell'affidabilità del meno affidabile di essi, che è il generatore, quindi: R < 0.99;

Per trovare un limite inferiore, ragioniamo sulla inaffidabilità F= 1 - R:

F = .

Poiché ancora : P(A B) min T F 0.01 + 0.02 = 0.03 T R

In definitiva, si ottiene:

0.97 < R < 0.99,

Nota: la precedente disuguaglianza che deve essere valida anche nel caso di componenti indipendenti (e infatti è così).

Domanda: Quale è l'importanza pratica di tale tipo di disuguaglianza?

Esercizio N° 2

Calcolare l'affidabilità del sistema precedente nel caso in cui venga aggiunta una terza linea di affidabilità P(L₃)=R₄ = 0.99, nel caso di eventi indipendenti; discutere la convenienza "pratica" di tale ridondanza.

Con l'aggiunta di una terza linea, nel caso di eventi indipendenti si ottiene:

P(S) = P[G (L₁ L₂ L₃)] = P(G ) P(L₁ L₂ L₃) = P(G )[1-P(]=

= P(G)[1-:

si è utilizzato il fatto che, se più eventi sono indipendenti, anche i loro complementari sono indipendenti. Come si vede, aggiungendo un componente in parallelo all'interno di un sottosistema (quello di trasmissione), l'affidabilità del sistema, come intuitivo, aumenta (dato che aumenta l'affidabilità del sottosistema). Poiché pero il sistema era già molto affidabile, l'aumento "relativo" di affidabilità è abbastanza modesto: esso in pratica converrà solo se l'installazione è poco costosa e/o la perdita del carico sarebbe molto gravosa (ad. es. perché è un carico preferenziale).

Esercizio N° 3

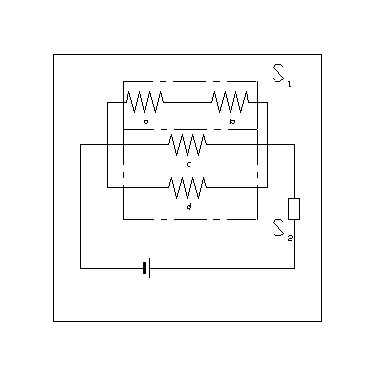Per il circuito in ura, formato da un generatore e da 4 resistenze (a,b,c,d), calcolare:

a) l'affidabilità R del sistema, sapendo che le resistenze a, b, c, d, si possono guastare solo per circuito aperto. Si supponga che A, B, C, D, siano indipendenti, e che P(A), P(B), P(C), P(D) = r = 0.98, dove:

A = ;B = ;

C = ;D = .

b) Indicando con S₁ il sottosistema formato dalla serie di (a,b), e con S₂ quello formato dal parallelo di (c,d), si calcoli la probabilità che a guastarsi sia il sottosistema S₁ e la probabilità che a guastarsi sia S₂ , nel caso in cui si sappia che il sistema S è guasto.

R = P(S) = P(S₁ S₂) = 1- P( ) = 1-P()P()   (*)

P()=1- P(S₁) = 1- P(A B) =1- P(A)P(B) = 0.0396

P() =1-P(S₂) = P( ) = P()P() = 0.0004

Sostituendo P() e P() nella(*) si ricava: R= 0.99998.

Si noti che essendo S₁ e incompatibili ed esaustivi, si poteva pervenire allo stesso risultato mediante la probabilità totale, condizionando S rispetto a S₁ e , ottenendo:

(**)

P(S|S₁) = 1 (perché se funziona S₁ necessariamente funzionerà anche S);

P(S|) = P(S₂) (perché se S₁ è guasto, S funzionerà solo se funzionerà S₂).

Sostituendo nella (**) si ottiene:

R=P(S)=P(S₁)+P()P(S₂) = 0.99998.

b)  La probabilità che a guastarsi sia il sottosistema S₁ nel caso in cui S è guasto [] si ricava immediatamente considerando che se S è guasto, necessariamente dovrà essere guasto anche S₁, quindi = 1; analogo discorso vale per .

Esercizio N° 4

Calcolare l'affidabilità del sistema S supponendo che tutti i componenti siano indipendenti e che p = P(G_i) = 0.98 e r = P(L_i) = 0.99.

Chiamando G e L i sottosistemi formati rispettivamente dai generatori e dalle linee, si ha:

R=P(S)=P(G L)=P(G)P(L) (1)

Il sistema G è un sistema parallelo parziale 2/3 (funziona se funzionano almeno due generatori), quindi: (2)

(3)

Sostituendo la (2) e la (3) nella (1) si ricava R = 0.99872.

Esercizio N°

Il sistema a lato è costituito da 6 componenti tutti indipendenti di affidabilità R_i. Calcolare la funzione di affidabilità strutturale, R_S ,del sistema.

Il sistema è coerente? Nel caso, lo si verifichi.

Per l'indipendenza dei componenti - e quindi dei sottosistemi - del sistema si può scrivere R_S = R_AR_B,

dove:   R_A = R₁R₂; R_B = R₃R₄ + R₅R₆ - R₃R₄R₅R₆;

R_S = R₁R₂[R₃R₄+R₅R₆-R₃R₄R₅R₆]

E' ovvio che il sistema è coerente, e per stabilirlo non c'è bisogno di alcun calcolo! Perché?

Esercizio N° 6

Un apparecchio A deve funzionare a tensione nominale rigorosamente costante; esso può guastarsi solo a causa di alimentazione non costante, e la probabilità di guasto P() è 0.05. Per proteggere l'apparecchio si vuole usare un monitor intelligente, il quale stacca l'alimentazione dell'apparecchio quando la tensione non è costante. La probabilità che il monitor fallisca l'intervento è P() = 0.10. (Ipotesi: il sistema è considerato funzionante quando l'alimentazione è staccata a seguito dell'intervento del monitor; il funzionamento del monitor è indipendente da quello della rete).

Il responsabile dell'acquisto fa la seguente considerazione: " non conviene comprare il monitor, in quanto P() > P()".

D'altro canto, un "esperto", consultato a tale proposito, ne sconsiglia anche lui l'acquisto, in quanto il sistema "rete + monitor" è di tipo serie, e quindi la sua affidabilità è minore dell'affidabilità di A e B presi singolarmente. Chi ha ragione?

La probabilità che il sistema non funzioni nel caso in cui si decide di non installare il monitor è P() = P() = 0.05, dove A è l'evento "buon funzionamento (a tensione costante) della rete di alimentazione. Se si decide, invece, di installare il monitor, il sistema si guasta se si guastano sia la rete che B; quindi si tratta di un sistema parallelo. Dunque, P() = P( ) = P()P() = 0.005, essendo A e B indipendenti. La probabilità di guasto nel secondo caso è minore, quindi l'affidabilità è aumentata. Quindi, nessuno dei due ha ragione. Capita . (e infatti questo è un fatto capitato).

Esercizio N° 7

Si consideri il sistema a lato. Le linee e gli interruttori sono gli unici componenti che si possono guastare. Costruire il diagramma di affidabilità nel caso che:

a) almeno un carico va alimentato e entrambe le linee possono, da sole, far fronte al carico;

b)Entrambi i carichi devono essere alimentati e ogni linea, da sola, riesce a far fronte al carico totale;

c) Entrambi i carichi devono essere alimentati e le singole linee non riescono a far fronte al carico totale (ma solo ad un singolo carico qualsiasi).

Il funzionamento del sistema può essere facilmente descritto con il metodo dei tie-set (o cut set); qui si presenta un ragionamento logico (probabilistico), che porta - come deve essere - allo stesso risultato.

a) Il sistema funziona se si verifica almeno uno dei seguenti eventi:

1) funziona l₁ e [b₁ o (b₂ e b₃)], cioè se si verifica: L₁ [ B₁ (B₂   B₃)];

2) funziona l₂ e [b₃ o (b₁ e b₂)], cioè se si verifica L₂ [ B₃ (B₁   B₂)].

Lo schema affidabilistico è dunque il seguente (verificarlo con il metodo dei Tie-Set):

Si noti che, ragionando sui percorsi che legano l'ingresso all'uscita, lo schema appena visto è perfettamente equivalente allo schema di tipo "ponte".

b) Affinché il sistema funzioni deve funzionare almeno una linea; se ne funziona una sola, devono necessariamente funzionare tutti gli interruttori; se funzionano entrambe, l'interruttore centrale può anche non funzionare. In definitiva, si ottiene il seguente schema (ricavabile semplicemente con il metodo dei Tie-Set):

c) b₁ e b₃ devono necessariamente funzionare, mentre b₂ può anche non funzionare. In definitiva, in questo caso si ha semplicemente la serie di (l₁ , l_{2 ,} b₁, b₃).

Esercizio N° 8

Calcolare l'affidabilità dell'ipotetico sistema in ura, in cui i componenti a e b sono "replicati" nei due rami

P(S) = P(S₁ S₂) = P[(A B) (A B)]

Poiché (A B) (A B), si ha semplicemente:

P(S) = P(A B); quindi, il sistema è equivalente al parallelo di a e b.

Provare a giustificare intuitivamente questo risultato

Esercizio N° 9

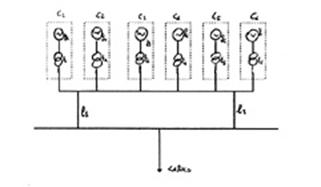
Calcolare l'affidabilità R_S del sistema nei seguenti casi:

a)   Il carico è deterministico ed il suo valore massimo è 95 MW; i generatori e i trasformatori sono tutti uguali tra di loro, sono indipendenti e si suppone che siano gli unici componenti che possono guastarsi; la loro affidabilità in un intervallo di tempo Dt è r_g = 0.97; r_t= 0.99;

b)   Anche le linee si possono guastare; r_l = 0.98 e P_l = 100 MW;

c)   

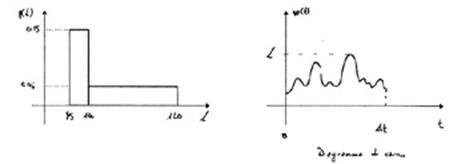
Il carico massimo è descritto da una variabile aleatoria la cui distribuzione di probabilità è rappresentata in ura.

Il carico può assumere solo valori interni gli intervalli L_A = 95÷ 100 MW e L_B = 101 ÷ 120 MW, con probabilità:

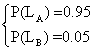
a)

Indicato con c_i il sottosistema costituito da g_i e t_i, e tenendo conto che tutti i componenti sono uguali tra di loro, si ottiene:

r_c = r_g r_t = 0.9603

Il sistema S è un sistema parallelo parziale 5 su 6 il cui schema affidabilistico è quello in ura;

la sua affidabilità vale (calcolarla anche senza utilizzare la formula Binomiale!):

b)

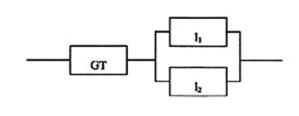Il sistema affidabilistico in questo caso diviene quello mostrato appresso, dove con GT si è indicato il sistema del caso precedente.

L'affidabilità in questo caso è:

c)

L'affidabilità del sistema S può essere calcolata attraverso la probabilità totale:

P(S) = P(L_A)P(S|L_A) + P(L_B)P(S|L_B) (*),

con: P(L_A)=0.95; P(L_B)=0.05

P(S|L_A) è l'affidabilità del sistema nel caso in cui il carico assume un valore compreso tra 95 e 100 MW; si è, quindi nelle stesse ipotesi di cui al punto 2), quindi P(S|L_A) = 0.97836.

P(S|L_B) è l'affidabilità del sistema nel caso in cui il carico assume un valore compreso tra 101 e 120 MW; in tal caso lo schema affidabilistico è costituito da tutti i componenti in serie si; quindi P(S|L_B) = .

Sostituendo nella (*) si ottiene: R = P(S) = 0.96710; si nota che esso è compreso tra P(S|L_A) e P(S|L_B).

Esercizio N° 10

Si supponga di avere un sistema di produzione di energia elettrica che alimenta tre città a, b, c. Il centro di produzione W è collegato direttamente ad a e b tramite due elettrodotti 1 e 2. Le tre città sono collegate tra loro dagli elettrodotti 3, 4, e 5. Calcolare l'affidabilità del sistema nell'ipotesi che gli elettrodotti siano indipendenti e uguali tra di loro. Particolarizzare per R_i = p = 0.90. Il sistema funziona se tutte le città sono alimentate.

Lo schema funzionale del sistema è il seguente:

Si può fare riferimento al seguente schema, perfettamente uguale, ma che permette una più facile visualizzazione del problema:

Si noti che lo schema così ottenuto non è un " sistema ponte", infatti non si tratta di uno schema affidabilistico! (vi sono tre "uscite" : i nodi a,b,c).

Condizionando rispetto ai seguenti eventi:

e applicando la probabilità totale, si ottiene:

   (1)

Calcolo di

Se funzionano le linee 1 e 2 lo schema diviene:

Le città a e b sono sempre alimentate, mentre la città c è alimentata se funziona la linea 4 o la linea 5, quindi = P( 4 5) (le linee 4 e 5 sono in parallelo). Detta q = 1 - p l'inaffidabilità del componente si ha:

= 1- q² (2)

Calcolo di

Se la linea 1 non funziona e la linea 2 funziona, lo schema diviene:

La città b è sempre alimentata, mentre le città a e c sono alimentate se funzionano almeno due delle tre linee 3, 4, 5; quindi il sistema è equivalente ad un parallelo parziale 2/3.

= (3)

Calcolo di

Se la linea 1 funziona e la linea 2 non funziona, lo schema diviene:

Per la simmetria del sistema, si può fare un discorso analogo al caso precedente, ottenendo:

= (4)

Calcolo di

Se la linea 1 e la linea 2 non funzionano lo schema diviene:

In tal caso, il centro di alimentazione e scollegato dal sistema di distribuzione, quindi:

= 0

Considerando che:

= p²

= p q

= q²

e sostituendo la (2), la (3) e la (4) nella (1), si ottiene:

R = P(S) = p² (1- q²) + 2p q ( )

Particolarizzando per p = 0.90 si ottiene:

R = P(S) = 0.97686

Esercizio N° 11

1) Risolvere il sistema in ura, nell'ipotesi che tutti i carichi vanno alimentati e che gli unici componenti che si possono guastare sono le linee; particolarizzare per R_i = p = 0.90.

Calcolare, inoltre:

2) P(3|S); P(1 2|S); P(4 5|S).

1) Ricordando che i generatori sono supposti sempre funzionanti, si può sostituire ad essi un generatore G di potenza pari a G₁ + G₂; in tal caso il sistema diviene affidabilisticamente uguale a quello delle tre città dell'esercizio precedente (già risolto!).

2.a)

(1)

Se la linea 3 funziona, il sistema diviene:

quindi:

P(S|3) = (2p - p²)² = 0.9801

P(3) = p = 0.90

P(S) = 0.97686

Sostituendo nella (1) si ha:

P(3|S) = 0.9030

2.b)

(2)

Se le linee 1 e 2 non funzionano, il sistema non funziona, quindi = 0. Sostituendo nella (2), si ricava che .

Analogo discorso per

Esercizio N° 12

Dedurre lo schema di affidabilità del sistema a lato, supponendo che:

entrambi i carichi vanno alimentati;

solo i componenti 1, 2, 3, 4, 5 sono soggetti a guasto;

tutte le linee hanno capacità adeguata ai carichi.

Particolarizzare il calcolo di R_S nel caso di linee uguali e indipendenti di affidabilità p = 0.90

L'affidabilità del sistema può essere calcolata con la probabilità totale, condizionando rispetto agli eventi 3 e :

R_S= P(S) = P(3)P(S|3) + P()P(S|)    (1)

Calcolo di P(S|3)

Supposta la linea 3 funzionante, il sistema risulta essere costituito dalle linee 1, 2, 4, 5 in parallelo:

ragionando in termini di inaffidabilità:

(2)

Calcolo di P(S|)

Nel caso in cui si suppone il componente 3 guasto, il sistema diviene un sistema serie di parallelo:

Facendo i dovuti calcoli risulta:

(3)

Sostituendo la (2) e la (3) nella (1) e ricordando che P(3) = p e P() = q, si ottiene:

Particolarizzando per p = 0.90 si ha:

R_S = 0.99792

Il problema si può risolvere in altro modo con il metodo dei cut-set.

Gli insiemi di taglio sono:

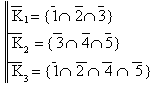
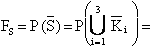
Trascurando i termini superiori al secondo, si ha:

quindi,

che coincide con il risultato trovato in precedenza a meno di una parte su 100.000

Volendo ricavare lo schema affidabilistico equivalente, si deve sfruttare la relazione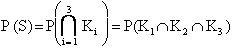

con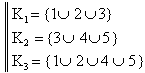

da cui:

Esercizio N° 13

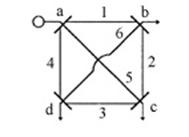Si consideri il sistema elettrico in ura, caratterizzato da un nodo di generazione (a) e 3 nodi carico (b, c, d).

Si vuole caratterizzare l'affidabilità del sistema rispetto all'alimentazione del nodo di carico b, nell'ipotesi che le linee (1, 2, 3, 4, 5, 6) di trasmissione possano non funzionare (gli altri componenti del sistema sono supposti funzionanti con certezza; si noti che ciò implica che gli eventuali prelievi di potenza da c e d non siano tali da sovraccaricare alcuna linea, in ogni condizione di funzionamento); si suppone che ogni linea, quando funzionante, abbia capacità tale da soddisfare il carico in b. dunque:

si derivi un possibile schema affidabilistico del sistema;

si calcoli l'affidabilità del sistema ipotizzando che le linee siano indipendenti, con uguale affidabilità p, e si particolarizzi al caso in cui p = 0.90

Condizionando rispetto agli eventi

si ottiene:

(1)

Calcolo di

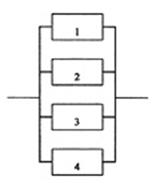Il sistema si riduce ad un parallelo di 4 componenti uguali, la cui affidabilità si può calcolare applicando la binomiale e ragionando in termini di inaffidabilità.

= q⁴, quindi

= 1- q⁴ (2)

Calcolo di

In tal caso il sistema si riduce al parallelo dei componenti 1 e 4:

(3)

Calcolo di

In tal caso il sistema si riduce al parallelo dei componenti 1 e 2:

(4)

Calcolo di

Il sistema diviene del tipo mostrato in ura:

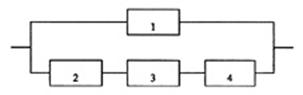Si ricava facilmente che:

(5)

Ricordando che: 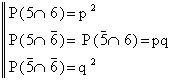   (6)

Sostituendo la (2), la (3), la (4), la (5) e le (6) nella (1) si ottiene:

Particolarizzando per p = 0.90, si ricava:

R = P(S) = 0.997848

L'affidabilità del sistema può essere calcolata anche con il metodo dei cut-set.

Gli insiemi minimi di taglio sono:

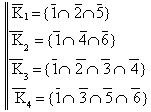
Quindi

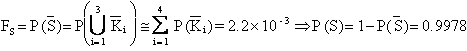
Come per l'esercizio precedente, si può ricavare uno schema equivalente:

5.10 ESERCIZI PROPOSTI

Provare a calcolare l'affidabilità di un sistema serie e di un sistema parallelo di due componenti con il metodo della probabilità totale, anche nel caso di componenti non indipendenti.

. Dati 2n componenti indipendenti e di uguale affidabilità p, discutere qualitativamente perché un loro collegamento secondo una struttura di tipo "SP" sia più affidabile - a parità di n e p - di una di tipo "PS". Provare a dimostrare tale proprietà analiticamente.

. Dato un sistema "PS" di 4 componenti indipendenti e di uguale affidabilità p, verificare che esso è più affidabile del singolo componente solo se p > p₁*= 0.618.

. Nelle stesse ipotesi dell'es. precedente, per un sistema "SP", si verifichi che p₁*=0.382.

. Dato un sistema di tre componenti (a,b,c) in "parallelo parziale" di tipo "2 su 3":

a) dimostrare - sia mediante i tie-sets che con l'algebra degli eventi - che esso è equivalente al parallelo di 3 sottosistemi serie, formati dalle 3 possibili coppie distinte [(a,b), (a,c) ,(b,c)] di componenti;

b) nel caso di componenti indipendenti e di uguale affidabilità p, discutere se e in che caso tale sistema sia più affidabile del singolo componente.

c) nelle stesse ipotesi di b), farne il confronto con un sistema parallelo di due componenti (cioè con il sistema "1 su 2" (discuterlo prima qualitativamente).

. Si fa l'ipotesi che un aereo funzioni se funziona almeno la metà dei suoi motori. Se essi sono indipendenti e di uguale affidabilità p, dimostrare che un quadrimotore è più affidabile di un bimotore se p > 2/3, altrimenti vale la proprietà opposta.

. Dato un sistema ponte, s, con elemento "trasversale" indicato con c (come nel par. 7), calcolare - nell'ipotesi di componenti indipendenti e di uguale affidabilità p - le probabilità:

P(c funziona | s funziona) e P(c guasto | s guasto).

Ripetere con uno qualsiasi degli altri componente. Spiegare il significato "pratico" di tali probabilità.

Si consideri ancora un sistema ponte come nell'es. precedente. Nell'ipotesi che sia p=½, provare a ideare un esperimento di "simulazione" del comportamento del sistema mediante successivi lanci di una moneta, e magari provare ad eseguire qualche simulazione per "stimare" il valore di affidabilità del sistema (si ricordi che il valore esatto è R = 0.5).