LA PROBABILITÀ DI UN EVENTO - Definizione classica (e "geometrica")

2.4 LA PROBABILITÀ DI UN EVENTO

Come già detto nella premessa, il concetto di probabilità è a tutti noto, almeno in termini intuitivi, e per comprendere ed interpretare i metodi e le applicazioni che si studieranno nel prosieguo può essere sufficiente affidarsi a tale concetto intuitivo. In base ad esso, dato un evento aleatorio A, con il termine "probabilità di A", indicato con P(A), si indica un numero che esprime la misura della "tendenza" a verificarsi di tale evento, oppure il grado di "veridicità" della proposizione espressa dall'evento, posto che non si possa decidere a priori se essa è vera o falsa, come già detto. Per convenzione, tale numero è compreso tra 0 e 1: 0 P(A) 1, e talvolta viene espresso in percentuale (ad es.: P(A) = 0.3 oppure P(A) = 30 %).

Attualmente, la probabilità di un evento viene definita mediante assiomi, presentati alla fine di questo paragrafo. E' opportuno tuttavia conoscere le diverse definizioni (o meglio "interpretazioni") della probabilità che si sono avute nel tempo:

Definizione "classica" (talvolta detta "a priori"), introdotta da Jacques Bernoulli nel 17° secolo, e poi generalizzata nella definizione "geometrica";

Definizione "frequentista" (detta anche statistica), legata al nome di von Mises (intorno alla metà del XX° secolo);

Definizione "soggettiva", sviluppata soprattutto dal matematico italiano Bruno de Finetti, pure nel XX° secolo.

Esse sono brevemente illustrate di seguito, e riprese anche più avanti (per una più estesa discussione di tali aspetti, si vedano i libri di Dall'Aglio, Papoulis, ecc. ). Innanzitutto, come si evince dal seguito, si nota che le prime due interpretazioni considerano la probabilità come una proprietà "oggettiva" dell'evento, mentre per i "soggettivisti" - come sono chiamati i seguaci della 3a interpretazione, essa dipende da colui che valuta la probabilità, ossia dal suo stato di informazione, ed è quindi appunto una proprietà "soggettiva".

1. Definizione classica (e "geometrica")

Secondo la definizione classica, "la probabilità P(A) di un evento A è il rapporto tra il numero dei casi favorevoli al suo verificarsi ed il numero dei casi possibili, purché essi siano tutti egualmente possibili".

Tale definizione ha lo svantaggio di essere "tautologica" (o ricorsiva), cioè di definire un concetto nuovo, quello di probabilità, tramite il concetto stesso che si sta definendo; questo avviene quando si parla di casi egualmente possibili, che poi vuol dire egualmente probabili. E' in base a tale concetto di probabilità che siamo soliti affermare, ad esempio: "nel lancio di una moneta la probabilità che esca "testa" è 0.5" . Ma, se vogliamo verificare se un componente elettrico funzionerà per un certo periodo, non possiamo certo affermare che la probabilità di tale evento è pari ad 1/2, pensando che ci sono due casi possibili (funziona o non funziona) e uno favorevole (funziona). Infatti, essendo il componente progettato e costruito per funzionare, i due casi evidentemente non sono equiprobabili!

Tuttavia tale definizione è utile quando si sia in condizioni di evidente simmetria, come nel caso appunto del lancio di una moneta, di un dado, del gioco del lotto; e non è infatti un caso che tale definizione sia stata sviluppata agli inizi della teoria, quando le sue applicazioni numeriche riguardavano appunto il gioco d'azzardo (il primo trattato di calcolo delle probabilità fu l' "Ars Conjectandi" di Bernoulli, apparso nel 1713. Ma già dal '500 alcuni matematici italiani avevano effettuato i primi calcoli probabilistici relativi ai giochi). Per alcune applicazioni, si rimanda la modulo sul calcolo combinatorio.

Originariamente, la definizione era relativa a spazi campione finiti, o comunque discreti (come appunto quelli relativi ai giochi), ma essa è naturalmente estensibile anche al "continuo", come si chiarirà con gli esempi che seguono (provare a dare una risposta prima di leggere la soluzione!):

Es. 2.4.1 (Incontro aleatorio) Una persona X ha un appuntamento alle 12 di un certo giorno con un'altra persona Y: supponendo che Y sia puntuale e aspetti al più 20 minuti, mentre X è un po' ritardatario e arriva "a caso" tra le 12 e le 13, quale è la probabilità che X e Y si incontrino?

In assenza di altre informazioni, bisogna presumere che il fatto che il signor X arrivi " a caso" nell'intervallo (0,60 minuti) a partire dalle 12 significa, come assumeremo per ipotesi, che egli può arrivare con uguale probabilità in tutti gli istanti compresi in tale intervallo, che costituisce appunto uno spazio campione "continuo" (ossia con la potenza del continuo), essendo formato da un intervallo di numeri reali (il tempo è infatti una grandezza continua, anche se nella sua rappresentazione ci fermiamo ai minuti, o ai secondi, ecc.).

E' allora naturale, posto Tx il tempo di arrivo di X a partire dalle 12, calcolare la probabilità dell'evento A in questione come:

P(A) = P(Tx < 20) = 20/60 =1/3

In questo caso abbiamo effettuato il rapporto tra la lunghezza dell'intervallo (0,20) - favorevole all'evento A - e la lunghezza dell'intervallo che definisce l'intero spazio campione. E' chiaro che in casi come questo il numero dei casi favorevoli ed il numero dei casi possibili sono entrambi infiniti, per cui il rapporto di cui sopra si trasforma naturalmente nel rapporto tra misure di intervalli, o più in generale di aree.

In generale, dato un insieme (spazio campione) W, discreto o continuo, si dice che un punto è preso "a caso" in W se, per ogni sottoinsieme A di B, la probabilità che il punto cada in A è data dal rapporto tra la misura di A e quella di W

P(A) = mis(A) / mis(W

A volte questa viene detta "probabilità geometrica", ma in effetti non differisce concettualmente da quella classica (la quale è un caso particolare di quest'ultima relazione). Si noti che, nel caso continuo non è in realtà corretto parlare di "risultati equiprobabili" (come abbiamo fatto a proposito degli istanti di arrivo) perché, proprio in base all'ultima definizione, la probabilità di ogni singolo risultato non può che essere nulla! (come la misura di un punto, che è un intervallo di lunghezza nulla); ad esempio, la probabilità che il signor X arrivi esattamente alle 12.00 (essendo questo inteso come numero reale) è evidentemente nulla, ma quella che arrivi tra le 12.00 e le 12.05 è pari a 5/60, così come quella che arrivi tra le 12.55 e le 13.00. L'equiprobabilità va allora in tal caso intesa nel senso che la probabilità di intervalli (o superfici) di uguale dimensione (misura) è sempre la stessa, indipendentemente da dove sia posizionato l'intervallo: si parla in tal caso di "probabilità uniforme".

Es. 2.4.2 (Incontro "doppiamente" aleatorio) Nelle stesse ipotesi di cui sopra, si supponga che anche la persona Y arrivi "a caso" tra le 12 e le 13; se il primo che arriva aspetta al più 20 minuti, quale è la probabilità che X e Y si incontrino?

Stavolta lo spazio campione è formato, nel piano delle coppie ordinate di numeri reali (Tx,Ty) rappresentanti rispettivamente gli istanti di arrivo di X e Y, dal quadrato definito dalla relazione:

W = ( 0< Tx < 60, 0 < Ty < 60)

Si lascia al lettore la "visualizzazione" dell'evento A in questione (ci si aiuti con un disegno), nonché la verifica del seguente calcolo della sua probabilità:

P(A) = [(60² - 40²)/ 60²] = 5/9

2. Definizione frequentista

Se l'esperimento aleatorio è ripetuto N volte - nelle stesse condizioni - e l' evento A si è presentato N_A volte, la sua frequenza relativa é definita dal numero f_N(A) = N_A /N, compreso tra 0 e 1; secondo la definizione frequentista (Von Mieses, 1928), "la probabilità P(A) dell'evento A è il limite della sua frequenza relativa quando il numero delle osservazioni N cresce indefinitamente":

Ad esempio, quando si dice che la probabilità che esca "testa" - nel lancio di una moneta - è di 1/2, nell'ambito di tale definizione si intende che, in un numero, n, sufficientemente alto di lanci, si verificherà "testa" all'incirca il 50% delle volte, e tale frequenza sarà sempre più prossima a 0.5 quanto più n si avvicina all'infinito. Questa definizione è evidentemente frutto della proprietà sperimentale nota come "legge dei grandi numeri", di cui si è già parlato. Tale definizione viene spesso adoperata in pratica per "stimare" la probabilità di un evento mediante la sua frequenza relativa su un numero "sufficientemente elevato" di prove effettuate nelle medesime condizioni.

La definizione vista presenta delle difficoltà sia dal punto di vista matematico (bisogna postulare l'esistenza di un limite associato ad una serie di prove sperimentali) che, soprattutto, da quello pratico (cosa significa "ripetere l'esperimento nelle stesse condizioni"? ciò implica la conoscenza e il controllo di tutti i fattori che possono influenzare il verificarsi dell'evento, il che appare piuttosto utopistico). Anche in questo caso, tuttavia, come accade per la definizione classica, si possono trovare delle applicazioni in cui il calcolo suggerito da tale definizione appare "ragionevole": esse sono quelle relative ad eventi che si possano ritenere "ripetibili", quali ancora quelli associati ai giochi, alle statistiche relative a popolazioni omogenee, ecc.

3. Definizione soggettiva

La probabilità soggettiva di un evento A è basata sulla esperienza o conoscenza del fenomeno da parte del "soggetto" che valuta tale probabilità; in base alla concezione soggettiva "la probabilità di un evento aleatorio A è un numero che misura il "grado di fiducia" che tale individuo ripone nel verificarsi dell'evento A". In pratica, è in base a tale concetto di probabilità che l'uomo comune effettua dei "pronostici" su eventi come "vittoria della tale squadra nella partita di Domenica prossima", oppure "Domenica pioverà": infatti questa definizione è l'unica che consente di trattare con eventi non ripetibili, nè "simmetrici", per i quali le precedenti interpretazioni cadono evidentemente in difetto. Sulla concezione soggettiva si tornerà più avanti, ma si può per il momento notare che essa è l'unica applicabile sempre. Prendiamo ad esempio il problema dell'"incontro aleatorio". Come si fa a stabilire che il signor X arriva "a caso" entro il tempo di un'ora di ritardo?

Certo non per "simmetria": normalmente (e auspicabilmente!) il ritardo di una persona non è "uniforme", ma si spera che ritardi piccoli siano più probabili di ritardi grandi, almeno se la persona si impegna per arrivare puntuale.

Neanche è molto realistico osservare il signor X tante volte, nelle stesse condizioni, e registrare i suoi ritardi. Se invece conosciamo il signor X, e abbiamo visto (magari in una sola occasione) che è poco puntuale, se ci dice "arriverò entro un'ora" e non abbiamo altre informazioni, è legittimo - in base al nostro stato di informazione, per quanto scarso possa essere - assumere che il suo ritardo sia "uniforme", e quindi la probabilità che arrivi 12.00 e le 12.05 ("puntuale") è pari a 5/60, così come quella che arrivi tra le 12.55 e le 13.00 ("molto in ritardo").

La teoria assiomatica

Si è già detto che la moderna teoria della probabilità prescinde da ogni interpretazione "filosofica" della probabilità, e quindi può essere utilizzata indipendentemente dalla interpretazione che lo studioso voglia dare al significato di probabilità. Essa infatti deduce, a assiomi di carattere generale, delle proprietà che sono accettabili per ognuna delle interpretazione sopra presentate. In effetti. la teoria assiomatica (stabilita dal matematico sovietico Kolmogorov nel 1933) si preoccupando semplicemente di definire une funzione di insiemi, P(A), che soddisfi a delle proprietà intuitive della probabilità, le più evidenti delle quali sono riportate di seguito:

1) P(W

P(

;

la P(A) è una funzione "crescente" degli eventi dello spazio campione, cioè: se A B, allora ci aspettiamo che sia: P(A) P(B); infatti, per dirla in maniera grossolana, i casi in cui si verifica B sono "più numerosi" di quelli in cui si verifica A.

Tutte queste, come altre, proprietà sono anche interpretabili geometricamente, mediante i diagrammi di Venn, se si associa alla probabilità di un evento la misura della sua area, avendo "normalizzato" ad uno l'area dell'intero spazio campione, come si ricava dalla definizione geometrica:

P(A) = mis(A)/mis(W

Si verifica facilmente (lo si faccia come esercizio) che tale particolare definizione rispetta le 4 proprietà sopra riportate.

L'impostazione assiomatica della probabilità si basa su tre assiomi presentati (in forma elementare) di seguito; si vedrà poi che la funzione P(A) così costruita soddisfa a queste e altre proprietà "intuitive". La cosa importante è che tali proprietà sono valide qualunque sia l'interpretazione che si dia della probabilità!.

Assiomi della probabilità

Sia dato uno spazio campione W relativo ad un dato esperimento aleatorio. Indichiamo con A W) "l'insieme delle parti di W", ovvero la famiglia di insiemi costituita da tutti i sottoinsiemi di W, compreso W e . Ad esempio se W , allora A W W

La probabilità P è una funzione degli eventi di W, e assume valori nell'intervallo reale (0,1). Una funzione di insiemi è detta "misura". Dunque, P è una misura che ha A W) come dominio e l'intervallo (0,1) come codominio. Formalmente, indicando con A l'insieme dei numeri reali:

P: A W A

In base alla teoria assiomatica, P(A) deve semplicemente soddisfare ai tre seguenti assiomi:

P(A) AIA W

P(W

Se A e B sono incompatibili (A B ), allora:

P(A B) = P(A) + P(B)    A,BIA W

Si noti che i primi due assiomi sono "banali". Il terzo è pure esso intuitivo, trovando giustificazione sia nella interpretazione classica che in quella frequentista. Ad esempio, se lo spazio campione è composto da N elementi, di cui x verificano l'evento A e y l'evento B, e gli eventi A e B sono incompatibili, è chiaro che - nell'ambito della interpretazione classica - si ha:

P(A) = x/N; P(B) = y/N; P(A B) = (x+y)/N = P(A) + P(B) (un esempio numerico relativo, ad esempio, al lancio di un dado, chiarisce subito questo fatto). Anche la sua interpretazione "geometrica" è immediata (se A e B sono disgiunti, l'area dell'unione è pari alla somma delle aree).

Da questi tre assiomi si ricavano le notevoli proprietà illustrate nel seguito.

2.5 PROPRIETÀ DELLA MISURA DI PROBABILITÀ

Dim. Dalla relazione , tenendo presente che , applicando il 2° e il 3° assioma si ricava l'asserto. Si noti che anche tale proprietà è banale: se, ad esempio, la probabilità che si verifichi l'evento "domani piove" è pari a 0.40, è naturale allora valutare che la probabilità che si verifichi l'evento "domani non piove" sia pari a 0.60. Tuttavia tale proprietà, nell'ambito della impostazione assiomatica, va dimostrata a partire dagli assiomi, che costituiscono il numero minimo di condizioni cui la probabilità deve soddisfare. Lo stesso ragionamento vale per le proprietà che seguono.

Dim. Dato che , poiché P(W) = 1, dalla relazione precedente segue l'asserto.

(Ricordiamo che gli eventi A_j si dicono incompatibili se A_j A_k= j k). Questa proprietà è una generalizzazione del terzo assioma, e si dimostra facilmente mediante la proprietà associativa. Ad esempio, nel caso di 3 eventi A,B,C incompatibili (A B= , A C= , B C= ), si ha: P(A B C)=P(A)+P(B)+P(C). Dim. Infatti, per la proprietà associativa, (A B C)=A (B C); si noti ora che: A (B C) = (proprietà ovvia, che può essere dimostrata mediante la proprietà distributiva). Quindi P(A (B C) ) = P(A) + P(B C). Dato che B C= , P(B C)=P(B)+P(C), da cui segue l'asserto. La generalizzazione a più eventi è immediata, e può essere dimostrata per induzione.

Tra quelle qui presentate, questa è la proprietà più importante. Si noti che, se A e B sono incompatibili, la 4. restituisce, come deve essere, il terzo assioma !. Anche questa proprietà, a ben vedere, può essere compresa intuitivamente, ad es. nell'ambito della interpretazione geometrica: se A e B non sono incompatibili, è noto che l'unione di A e B comprende tutti gli elementi di A e tutti quelli di B, compresi quelli dell'intersezione di A con B, considerati una sola volta. Se noi associassimo a tale evento la somma delle probabilità P(A) + P(B), è come se contassimo "due volte" gli elementi della intersezione (ci si può aiutare con un diagramma di Venn per capire meglio questo fatto): dunque, occorre sottrarre, da tale somma, la probabilità dell'intersezione, per avere la probabilità dell'unione. Naturalmente questa non è una dimostrazione. Prima della dimostrazione, vediamo un esempio numerico elementare. Consideriamo ancora l'esempio 1 relativo al lancio del dado, e assumiamo valida la definizione classica di probabilità : essa è in questo caso ragionevole, se si suppone che il dado sia bilanciato, oppure se non abbiamo conoscenza del dado, cosicchè per noi tutti i risultati elementari sono egualmente probabili, in assenza di informazioni contrarie (dunque, in questo caso l'interpretazione classica e quella soggettiva coincidono dal punto di vista numerico).

Esempio 1. (v. par. precedente). Abbiamo definito gli eventi A = [numero pari], B = [numero maggiore di 3], e già visto che A B = , A B = , quindi - nell'ipotesi di equiprobabilità - dovrà essere: P(A B) = 4/6.

Verifichiamo la validità della 4. Poiché: P(A) = 3/6 = P(B); P(A B) = 2/6, si ha:

P(A) + P(B) - P(A B) = 3/6 + 3/6 - 2/6 = 4/6 = P(A B).

Per dimostrare la 4., utilizziamo come lemmi le proprietà 5.1. e 5.2. (di minore importanza) di seguito esposte.

Dim. Utilizziamo la relazione di decomposizione: A = (A B) (AB); come già detto, a secondo membro si ha l'unione di eventi incompatibili, per cui si può calcolare la probabilità di tale unione mediante il terzo assioma. Si può allora scrivere: P(A) = P(A B) + P(AB). Segue l'asserto.

Dim. Utilizziamo l'altra relazione di decomposizione: A B = (AB) B; essendo (AB) B= , si può scrivere: P(AB)+P(B) = P(A B). Segue l'asserto.

(Nota: per verificare intuitivamente le proprietà 5.1. e 5.2, si faccia uso della probabilità geometrica: ad esempio, è intuitivo che per ottenere l'area di "A meno B" bisogna sottrarre all'area di A quella dell'intersezione tra A e B).

Infine, per dimostrare la 4., basta eguagliare i secondi membri delle relazioni 5.1. e 5.2. Si noti l'importanza del terzo assioma: su di esso sono basate le proprietà 3.-5.

Dimostriamo, infine, un'altra notevole proprietà, ovvero la "crescenza" della misura di probabilità, già discussa.

Dim. Si può utilizzare anche in questo caso la 5.1. Notiamo infatti che, se B A, allora A B = B; quindi dalla 5.1.: P(AB) = P(A) - P(B); essendo AB un evento, per il primo assioma la sua probabilità deve essere non negativa: da ciò segue l'asserto.

Si noti che, in generale, dalla 5.1. si ricava che P(A) P(A B): quest'ultima relazione può essere in effetti considerata un caso particolare della 6., dato che A B A, per ogni coppia di eventi A e B.

Probabilità dell'unione di più eventi

La proprietà 5. può essere generalizzata a più di due eventi. Ad esempio, nel caso di tre eventi (A,B,C), si ottiene:

Dim. Per la proprietà associativa, A B C = A (B C) = A D, dove D = B C; quindi:

P(A B C) = P(A D) = P(A) + P(D) - P(A D) (*); ora:

P(D) = P(B) + P(C) - P(B C) (**); P(A D) = P((A B) (A C)) = P(A B) + P(A C) + P((A B) (A C)) = P(A B) + P(A C) + P(A B A C) (***)

Sostituendo la (**) e la (***) nella (*) si ha: P(A B C) = P(A) + P(B) + P(C) - P(A B) - P(A C) - P(B C) + P(A B C). Si noti che anche in questo caso, se A, B, C sono incompatibili, si ritrova la proprietà: P(A B C)= P(A) + P(B) +P(C).

Nel caso di un numero qualsiasi, n, di eventi, si ha:

Tale relazione (di cui si omette la dimostrazione) può essere dimostrata per induzione, con una tecnica analoga a quella vista precedentemente. Si noti che essa restituisce come casi particolari la 3. e la 7.1.; inoltre, se gli eventi A sono incompatibili, si ritrova la proprietà 3.

In generale, i termini della somma a secondo membro della 7.2. sono 2ⁿ - 1, come si può dimostrare con il calcolo combinatorio; ad esempio, per n=3, si hanno 8-l = 7 termini, come appunto nella 7.1.

Nota sul calcolo della probabilità: differenza tra probabilità e statistica

Dalle precedenti relazioni si nota che il calcolo delle probabilità non insegna a calcolare le probabilità, ma solo a trasformarle. Ad esempio note P(A) e P(B), e nota P(A B), si risale a P(A B), come fatto nell'esempio 1; tuttavia, P(A), P(B) e P(A B) devono essere già note. Ciò non deve lasciare perplessi, in quanto è del tutto analogo a quanto accade in altre discipline scientifiche, come l'Elettrotecnica: questa insegna - ad esempio - come si calcola la resistenza equivalente di un circuito, note quelle dei singoli rami: ma queste ultime devono essere note a priori, ovvero si suppongono già misurate (e la misura del loro valore no è argomento specifico dell'Elettrotecnica).

Il calcolo della probabilità di un evento è effettuato su base sperimentale attraverso la statistica o su considerazioni a priori. Per esempio, nel caso del lancio di una moneta, dire che la probabilità che esca testa è ½ è un ipotesi comunque soggettiva, per quanto ragionevole. Se si lancia una moneta, e, per esempio, su mille lanci la testa esce meno di 50 volte l'ipotesi fatta prima si rivelerà (probabilmente..) sbagliata; se, invece, la testa esce tra 495 e 505 volte, si può ritenere ragionevole l'ipotesi P(T)= ½ anche se non è detto che essa sia vera: ci sono degli appositi test statistici che consentono di verificare sperimentalmente la validità di una ipotesi teorica.

In altri termini , non esiste alcun "teorema" che ci consenta di affermare a priori, ad esempio, che la probabilità dell'evento "testa" è pari ad ½. In pratica, la probabilità su un dato spazio campione va appunto "stimata" sulla base di prove sperimentali (ovvero su base statistica), oppure sulla base di ipotesi soggettive, più o meno ragionevoli, basate sull'esperienza passata del soggetto che formula l'ipotesi, ovvero sull'osservazione di fenomeni analoghi.

Introduciamo a questo punto la esposizione di alcune notevoli disuguaglianze (valide per ogni insieme di eventi considerati, appartenenti allo steso spazio campione); esse - ma questo vale per tutte le formule che qui si incontrano - non vanno imparate a memoria ma capite, in modo da saperle usare al momento giusto (cosa non sempre facile!); in ogni caso, per una migliore comprensione si consiglia il lettore di studiarsene la dimostrazione, o - meglio ancora - di cercare di abbozzarla prima di leggerla.

2.6 DISUGUAGLIANZE NOTEVOLI.

8.1 P(A B) min

Infatti, come già visto in margine alla propr. 6., P(A B) P(A) e P(A B) P(B), da cui l'asserto. In termini affidabilistici, la 8.1. afferma il fatto, intuitivo, che l'affidabilità di un sistema serie è sempre inferiore (o, al più, uguale, ma questo in pratica non succede mai) all'affidabilità di ogni singolo componente del sistema (e quindi del componente meno affidabile). Si noti che tale relazione è soddisfatta dalle probabilità dell'esempio 1. Essa è facilmente generalizzabile a più eventi.

8.2. P(A B) max

La dimostrazione è analoga a quella del caso precedente; infatti si ha:

A A B e B A B, da cui, per la 6.: P(A) P(A B) e P(B) P(A B), da cui l'asserto. In termini affidabilistici, la 8.2. afferma il fatto, intuitivo, che l'affidabilità di un sistema parallelo è sempre maggiore o al più uguale all'affidabilità di ogni singolo componente del sistema (e quindi del componente più affidabile). Si noti che tale relazione è soddisfatta dalle probabilità dell'esempio 1. Essa è facilmente generalizzabile a più eventi.

8.3.

Questa proprietà è immediata per n=2, come si ricava dalla proprietà 4. La dimostrazione generale si ricava facilmente per induzione; ad esempio, nel caso di tre eventi (A,B,C), si ha:

P(A B C) = P(A D), dove D = B C; poichè: P(A D) P(A) + P(D) e: P(D) P(B) + P(C), allora: P(A B C) P(A) + P(B) + P(C).

Naturalmente la 8.3. diviene una uguaglianza se (e solo se) gli eventi in questione sono incompatibili. Inoltre, essa è banale nel caso in cui la somma delle probabilità a secondo membro sia maggiore o uguale ad 1.

8.4.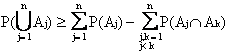

Questa disuguaglianza si ricava dalla probabilità dell'unione generalizzata, considerando solo le prime due sommatorie (si omette la dimostrazione). La 8.2., la 8.3. e la 8.4. sono utili per stabilire, ad esempio, un limite superiore ed uno inferiore alla affidabilità di un sistema parallelo, nei casi in cui sia difficile calcolarne il valore esatto.

8.5.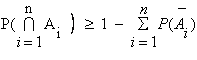

Questa disuguaglianza si ricava dalla 8.3., applicando la formula di De Morgan. La 8.1. e la 8.5. sono utili per stabilire un limite superiore ed uno inferiore alla affidabilità di un sistema serie.

Esempio affidabilistico

Si consideri un sistema "serie" formato da due componenti di uguale affidabilità (probabilità di buon funzionamento) pari a 0.99: si verifichi che l'affidabilità del sistema, R, è compresa nell'intervallo (0.98, 0.99). Si vedrà in seguito che, se i componenti sono indipendenti, la affidabilità del sistema è data dal prodotto delle affidabilità, e quindi vale R = (0.99)² = 0.9801, numero che rientra - come deve essere - nel precedente intervallo.

2.7. EVENTI NULLI ED EVENTI "QUASI CERTI"

Sappiamo che la probabilità dell'evento impossibile è nulla; ci domandiamo: è vero l'inverso? ovvero: se P(A) = 0, possiamo dire che A è impossibile?. La risposta, in generale, è no! Notiamo infatti innanzitutto che la probabilità, essendo una funzione ( i cui elementi sono eventi di uno spazio campione), è in generale univoca, ma non biunivoca. Ossia, ad ogni dato evento A, la funzione probabilità assegna un unico valore, P(A). Tuttavia, due eventi con la stessa probabilità non necessariamente coincidono. Ad esempio, nel caso dell'esempio 1, gli eventi A = [numero pari] e B = [numero maggiore di 3] hanno, nelle ipotesi fatte, la stessa probabilità (pari a 0.5). Tuttavia, essi non sono uguali!

Con lo stesso ragionamento, possiamo dire che dal fatto che P(A) = 0 non si può dedurre: A =

Analogamente, dal fatto che P(A) = 1 non si può dedurre: A = W. Diremo allora che:

Se P(A) = 1, l'evento A è detto "evento quasi certo".

Se P(A) = 0, l'evento A è detto "evento nullo" (ovvero, il complementare di A è "quasi certo").

In generale, nel calcolo delle probabilità, una proprietà definita su un dato spazio campione è detta "quasi certa" se si verifica con probabilità pari ad 1, ovvero se l'insieme degli elementi che non verifica tale proprietà è un evento di probabilità zero (o, nel linguaggio della teoria della misura, un insieme di "misura nulla"). Tale espressione è analoga al "quasi ovunque" dell'analisi matematica.

Per chiarire questo fatto consideriamo il seguente esempio: supponiamo di estrarre a caso un numero del lotto: la probabilità che si verifichi un dato numero, per esempio il 34, è pari a 1/90, nell'ipotesi di equiprobabilità. Nella stessa ipotesi, supponiamo di estrarre a caso un numero da un insieme infinito, ad esempio dall'insieme dei numeri naturali (si immagini un gioco del lotto con infiniti numeri), o dall'insieme dei numeri reali (si immagini di rilevare, con uno strumento di precisione infinita, la corrente su un conduttore la cui resistenza sia incognita). Chiaramente, se tutti i numeri sono equiprobabili, in tal caso il comune valore di tale probabilità non può che essere nullo (il numero di casi "favorevoli" è 1, il numero di casi possibili è infinito). Tuttavia, ciò non vuol dire che che un dato numero (ad es., il numero 34 nel primo esempio, o il valore "34 Ampere" nel secondo) non venga mai estratto (altrimenti, ragionando così per ogni numero, dovremmo concludere che .. nessun numero può essere estratto!). In effetti, come si vedrà nello studio delle variabili aleatorie continue (come la corrente nel secondo esempio), è possibile assegnare la probabilità su uno spazio campione continuo (come l'insieme dei numeri reali) in modo tale che la probabilità di un singolo elemento sia nulla, eppure gli assiomi della probabilità siano soddisfatti (ad esempio la probabilità dell'intero spazio campione sia unitaria). Per quanto questo ragionamento appaia (giustamente) piuttosto astratto, si deve notare che, nella pratica non si presenta mai la necessità di valutare la probabilità di un evento costituito da un un unico elemento di uno spazio campione avente la potenza del continuo: ad esempio, nel caso della misura di corrente, è impossibile verificare in pratica che la corrente assuma il valore I = 34 Ampere, considerato come numero reale (ossia il numero 34.00000 con infiniti zeri dopo la virgola), vista l'impossibilità di disporre di uno strumento di precisione infinita. Del resto, nella pratica ingegneristica non si lavora mai con i numeri reali, ma con un sottoinsieme finito - sia pure molto grande - di essi, a causa dell'inevitabile errore di misura o di rappresentazione (arrotondamento).

2.8 INDIPENDENZA STATISTICA.

Il concetto di indipendenza statistica è di fondamentale importanza nel calcolo delle probabilità: esso verrà ripreso anche dopo aver introdotto il concetto di probabilità condizionata.

Come concetto, due eventi sono indipendenti quando il verificarsi di uno di essi non influenza la probabilità di verificarsi dell'altro. La definizione di seguito enunciata serve appunto ad esprimere, come sarà chiaro nel seguito (vedi paragrafo sulla probabilità condizionata), tale concetto.

Definizione Due eventi A,B si dicono (statisticamente) indipendenti se P(A B)=P(A)P(B).

(Nota: spesso nel seguito l'avverbio "statisticamente" verrà omesso per brevità)

Ricordiamo che invece che due eventi A e B si dicono incompatibili se A B= . Si noti che l'incompatibilità è una proprietà legata agli eventi, quindi può essere dedotta dai diagrammi di Venn; l'indipendenza è invece legata alla probabilità degli eventi, per cui la si può evincere solo dal calcolo.

Esempio

Consideriamo due lanci successivi di un dado, di una moneta, o successive estrazioni di un numero al lotto, ecc.: è intuitivo aspettarsi che i successivi risultati siano indipendenti. Vediamolo in un esempio relativo a due lanci di una moneta: ossia consideriamo l'esperimento aleatorio E "doppio lancio di una moneta", essendo interessati al risultato di testa (t) o croce (c). Si verifichi che - nell'ipotesi di equiprobabilità - gli eventi:

T₁ = [testa al primo lancio] e T₂ = [testa al secondo lancio]

sono indipendenti

Soluzione: si considerino i due spazi campioni relativi al primo ed al secondo lancio, rispettivamente W e W ; chiaramente, W == , W == . Lo spazio campione relativo al doppio lancio è dato dal prodotto sectiunesiano:W W W = . Assumendo l'equiprobabilità, questi quattro risultati hanno tutti probabilità pari ad ¼.

Si tratta ora semplicemente di applicare la definizione, andando a vedere quale sia l'evento intersezione e quale sia la sua probabilità: si ha T₁ = ; T₂ = e dunque:

T₁ T₂ =

Ora, poiché evidentemente: P(T₁ ) = 1/2 = P( T₂ ) e P( T₁ T₂ ) = 1/4 , la proprietà di indipendenza è soddisfatta.

Indipendenza dei complementari

Vale la seguente importante proprietà: "se A e B sono due eventi indipendenti, lo sono anche"; anche questa proprietà è ragionevole: ad esempio, in affidabilità, se il funzionamento del componente "a" (evento A) non dipende dal funzionamento del componente "b" (evento B), è logico attendersi che non dipenda neanche dal guasto di "b" (evento ).

Dim. Siano A e B indipendenti. Per verificare che sono indipendenti si deve dimostrare che ; infatti:

=.

In modo analogo si dimostra l'indipendenza per le altre due coppie (l'indipendenza dei complementari si può dimostrare anche con la formula di de Morgan).

Esempio

Un sistema è formato da due componenti, a e b, aventi rispettivamente affidabilità 0.90 e 0.80. Si calcoli - nell'ipotesi di indipendenza degli eventi di funzionamento - la probabilità che

a)  almeno uno dei componenti funzioni

b)  almeno uno dei componenti si guasti

Un semplice modo di calcolo, che utilizza l'indipendenza, è quello schematizzato di seguito (il lettore provi a formalizzarlo introducendo gli operatori di unione, intersezione, negazione, ecc.):

a)  P(almeno uno dei componenti funziona) = 1- P(sono entrambi guasti) = 1 - (0.1)(0.2) = 0.98.

b)  P(almeno uno dei componenti si guasta) = 1- P(sono entrambi funzionanti) = 1 - (0.9)(08) = 0.28.

Si nota che al punto a) viene calcolata l'affidabilità del sistema nel caso in cui esso sia di tipo "parallelo"; la punto b) viene calcolata l'inaffidabilità (probabilità di guasto) del sistema nel caso in cui esso sia di tipo "serie": si noti che nel caso a) si è utilizzata la indipendenza degli eventi di guasto, che discende - in base alla proprietà suddetta - da quella degli eventi di funzionamento

Indipendenza di più eventi

Tre eventi A,B,C si dicono indipendenti se valgono le seguenti 4 relazioni: 

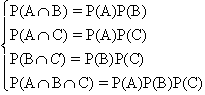
Generalizzando, si può dire che gli eventi sono indipendenti se valgono le seguenti relazioni: , r I (1,2, ..n-l), s I (r+2,..,n)

Cioè, più semplicemente, se le probabilità di ogni possibile intersezione (a due a due, a tre a tre, ecc.) è uguale al prodotto delle probabilità dei singoli eventi componenti. (Nota: il numero delle relazioni può essere ricavato dal calcolo combinatorio; nel caso di tre eventi esse sono in numero pari a:

2³- (3+1) = 8 - 4 = 4, come sopra visto).

Anche nel caso di più eventi vale la indipendenza dei complementari, come generalizzazione della proprietà già vista nel caso di sue eventi (si omette la dimostrazione)

Esempio

Un sistema è formato da dieci componenti, tutti aventi affidabilità 0.90. Si calcoli - nell'ipotesi di indipendenza degli eventi di funzionamento - a) la probabilità che almeno uno dei componenti si guasti, b) l'affidabilità del sistema se i componenti sono connessi in "parallelo".

Soluzione:

a)  P(almeno uno dei componenti si guasta) = 1- P(sono tutti funzionanti) = 1 - (0.9)¹⁰

b) Affidabilità del sistema parallelo = P(almeno uno dei componenti funziona) = 1- P(sono tutti guasti) = 1 - (0.1)¹⁰ = 1 - 1E-l0.

(Si è utilizzata l'indipendenza dei guasti)

Nota: l'affidabilità del sistema parallelo così composto è elevatissima (praticamente unitaria), anche se la probabilità che si verifichi almeno un guasto è molto elevata: si discuta questo fatto.

2.9 PROBABILITÀ CONDIZIONATA

Dati due eventi, A e B, di uno stesso spazio campione, supponiamo di voler valutare la probabilità che si verifichi l'evento A, nell'ipotesi che si sia verificato l'evento B: tale probabilità è chiamata probabilità condizionata di A nell'ipotesi B, o "probabilità di A condizionata a B" ed è indicata con P(A|B). In generale, il fatto che B si sia verificato modifica il nostro stato di informazione (ovvero la nostra incertezza rispetto ai possibili risultati dello spazio campione), e quindi è ragionevole utilizzare tale informazione per "aggiornare" la nostra valutazione di probabilità di A. Si consideri ancora un esempio calcistico: una squadra "a" gioca una partita di calcio contro un'altra squadra b, e sia A = [a vince la partita], V = [a è in vantaggio al termine del primo tempo]; in assenza di informazioni, potremmo valutare la probabilità di A con un dato numero, ad esempio 1/3 se non sappiamo nulla delle due squadre o se riteniamo i tre possibili risultati (vittoria, pareggio, sconfitta) equiprobabili. Se però siamo informati che si è verificato l'evento B, il nostro grado di fiducia nel verificarsi di A probabilmente aumenterà (ossia saremo disposti a scommettere una somma maggiore su di esso), per cui valuteremo (sulla base di opportune statistiche o di valutazioni soggettive) P(A|V) maggiore di P(A), ad esempio P(A|V) = 2/3 = 2P(A). Sia invece B=[b vince contro a]: è chiaro che se B si è verificato, non può verificarsi anche A (A e B sono chiaramente incompatibili, se a gioca contro b!), ci aspettiamo allora che sia P(A|B)=0. Infine consideriamo un'altra partita, giocata contemporaneamente da altre due squadre, "c" e "d", e sia C = [c vince contro d]: se riteniamo che il la vittoria di non influenzi la probabilità di vittoria di A (perché, ad esempio, a mentre gioca non conosce il risultato di c, oppure perché non sono rivali per lo "scudetto" o la "retrocessione") - il che vuol dire che riteniamo gli eventi A e C statisticamente indipendenti - allora, se sappiamo che C è vero, la nostra valutazione di probabilità di A non varierà, e quindi sarà P(A|C) = P(A).

In generale, è naturale richiedere che la probabilità di A condizionata a B rispetti le seguenti proprietà intuitive:

Se A e B sono incompatibili, P(A|B) = P(B|A) = 0

Se A e B sono indipendenti, P(A|B) = P(A), e P(B|A) = P(B)

Introduciamo dunque la definizione di probabilità di A condizionata a B:

Si noti che la probabilità di A condizionata a B è definita solo se B ha probabilità non nulla!

Si noti ancora che la P(A|B) definisce la probabilità dell'evento A, dato che B si è verificato, e non la probabilità dell'evento "A|B" (non si definisce un "evento condizionato").

La (1) rispetta le proprietà sopra introdotte (vedi seguito). Vediamo con un semplice esempio come essa esprima il significato concettuale di probabilità condizionata. Consideriamo ancora l'esempio 1 relativo al lancio del dado, con: A = [X pari], B = [X>3]. Ci chiediamo quale sia la P(A|B), nell'ipotesi di probabilità uniforme; se X>3, i casi favorevoli ad A sono 2 (i risultati 4 e 6), quelli possibili sono 3 (4,5 e 6), quindi ci aspettiamo che sia P(A|B) = 2/3. Se applichiamo la definizione (1), vediamo che tale risultato intuitivo è confermato dal calcolo.

E' facile rendersi conto di perché la definizione di probabilità condizionata sia data mediante la (1), facendo ad esempio riferimento alla interpretazione frequentista.

Esempio

Si consideri un mazzo di sectiune napoletane: si estrae a caso una carta e poi, senza rimettere la prima nel mazzo, una seconda carta. Sapendo che la prima era un asso, quale è la probabilità che anche la seconda sia un asso?.

Si lascia al lettore verificare il seguente risultato, ottenuto mediante il concetto di probabilità condizionata; i simboli sono evidenti:

P(B|A) = 3/39 = 1/13; si noti che P(B) = 1/10: dopo l'estrazione di un asso, è chiaro che la probabilità che anche la seconda carta sia un asso sarà minore: infatti è naturale che, in assenza di rimessa nel mazzo, i due eventi non siano indipendenti.

Si provi, per esercizio, a calcolare tale probabilità condizionata anche mediante la definizione (si richiede qualche considerazione di calcolo combinatorio)

Verifichiamo ora che tale definizione - come è doveroso - rispetta, al variare dell'evento A, gli assiomi di Kolmogorov, ossia che P(A|B) definisce effettivamente una probabilità:

A, A₁, A₂, B IA W) si ha infatti, come si dimostra facilmente:

P(A|B)

P(W|B) = 1  (2)

P((A₁ A₂)|B) = P(A₁ |B) + P(A₂ |B), se A₁ A₂=

Quest'ultima proprietà si dimostra applicando la definizione e la proprietà distributiva.

Proprietà notevoli della probabilità condizionata

Valgono ancora le seguenti proprietà, peraltro intuitive, di facile dimostrazione:

P(A|W) = P(A)

P(W|A)= P(W); P( |A)=P(

Questa è una ulteriore dimostrazione del fatto che l'evento certo e l'evento impossibile sono indipendenti da ogni altro evento.

Se A e B sono incompatibili, P(A|B) = P(B|A) = 0 (come anticipato)

Infatti in tal caso la intersezione di A e B è l'evento impossibile.

Se A e B sono indipendenti, P(A|B) = P(A), e P(B|A) = P(B) (come anticipato)

Come già detto, questo chiarisce meglio il concetto di eventi (statisticamente) indipendenti: se si verifica B, ciò non muta la nostra informazione riguardo alla probabilità di B, e quindi deve essere P(A|B) = P(A); la proprietà di indipendenza è chiaramente simmetrica, e quindi è anche P(B|A) = P(B).

Se B A, allora: P(A|B)=1

Anche tale proprietà è intuitiva: infatti, se si verifica B, ci aspettiamo che si verifichi certamente anche A, visto che B implica A .

P(|B) = 1 - P(A|B)

Dim. Per la 3. si ha: P(A |B) = P(A|B)+P(|B); poiché A =W, si ottiene:

P(W|B)=P(A|B)+P(|B). Dalla 2. si deduce P(W|B)= 1; segue l'asserto.

Si faccia però attenzione al fatto che, in generale, risulta: P(A|B)+P(A|) 1; ad esempio, nel caso particolare di A=W, si ha:    P(W|B) + P(W|) = P(W) + P(W) = 2 !, qualunque sia l'evento B (con probabilità > 0).