 |  |
| |
 |
tecnica |
|
CAPITOLO 6
RISPOSTA IN FREQUENZA DEGLI AMPLIFICATORI
Definiamo funzione di trasferimento F(s) il
legame esistente tra la trasformata di Laplace del segnale di uscita e la
trasformata del segnale in ingresso ( 6.1).
La funzione F(s) è indipendente dal tipo di segnale applicato, ma dipende solo dalla costituzione del sistema, quindi siamo in grado di individuare e caratterizzare il comportamento del sistema stesso studiando tale funzione.
Nota: si tratta di una funzione complessa di variabile complessa, in altre parole F(s) è un numero complesso x+jy e la variabile s è un numero complesso s + jw
Esempio 1
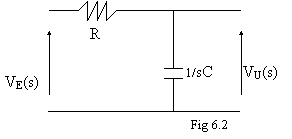
La funzione F(s), rafurata in . 6.3,
presenta un polo nel semipiano negativo di s
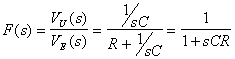
Esempio 2
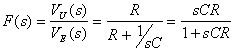
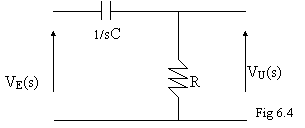
La funzione F(s), rafurata in .6.5, presenta un polo e uno zero:
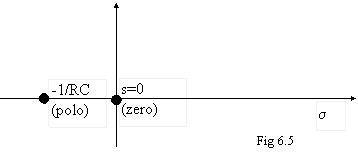
Normalmente abbiamo la seguente sequenza di operazioni:
Noi, invece, ci limiteremo a "estrarre" da F(s) il comportamento della rete in regime sinusoidale; uso le informazioni presenti in F(s) (posizione dei poli e degli zeri) per capire come si comporta la rete in regime sinusoidale, in modo da poter tracciare la CURVA DI RISPOSTA.
In regime sinusoidale, la variabile s contiene solo la parte immaginaria: s= jw, per cui studieremo la funzione complessa F(jw), in altre parole studieremo la sua fase e il suo modulo (che dipendono da w
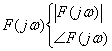
Se in ingresso ho uno stimolo sinusoidale, vista la linearità delle reti che consideriamo, anche in uscita avrò la stessa sinusoide, a meno di differenze sull'ampiezza e sulla fase:
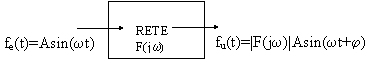
(dove j=fase di F(jw
Come possiamo osservare, non cambia la frequenza della sinusoide di ingresso, ma il modulo della funzione di trasferimento va a modificare l'ampiezza della sinusoide mentre la fase della funzione di trasferimento va a modificare la fase della sinusoide.
NOTA: w pf [w=rad/sec e f=1/sec=Hz].
Esempio:
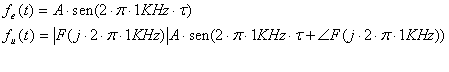
Questi diagrammi si chiamano CURVE DI RISPOSTA e vengono disegnati su diagrammi di Bode; nei diagrammi di Bode, all'asse x è applicata una scala logaritmica in base 10, sull'asse y è applicata una scala in decibel per quanto riguarda il modulo ( 6.6), una scala normale per quanto riguarda la fase ( 6.7).
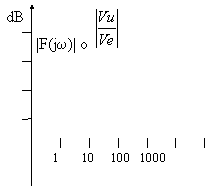
MODULO:
NOTA: in dB si esprimono solo rapporti e non grandezze singole. Definizione di decibel:
Definizione
originale: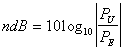 
(Pu,Pe=Potenza in uscita, entrata)
Definizione per le
tensioni: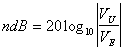 
(Vu,Ve=tensione
in uscita, entrata)
Esempi:
se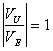 
allora 0 dB se
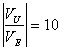allora 20 dB
se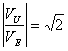 
allora 3 dB se
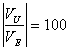allora 40 dB
se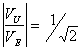 
allora -3dB
Se il modulo del rapporto è inferiore ad 1 avremo in dB un valore negativo, altrimenti, se il modulo del rapporto è maggiore di 1, avremo in dB un valore positivo. Nota che ad ogni aumento di 20 dB, il modulo si decuplica.
FASE:
Una generica F(s) è una funzione razionale fratta propria:
dove il grado del polinomio al numeratore è sicuramente inferiore, al più uguale, al grado del polinomio al denominatore, quindi il numero di zeri è minore o uguale al numero dei poli. Inoltre, per una condizione di fisica realizzabilità, i poli si devono trovare nel semipiano negativo di s
I polinomi possono essere rappresentati come prodotti di termini di 1° grado, per esempio:
quindi, in generale, avremo che F(s) si presenta in questa forma:
con m n.
Le soluzioni ai ed ai posssono essere reali o complesse; nel secondo caso, siccome i polinomi sono a coefficienti reali, queste soluzioni sono complesse coniugate. Per cui potrò avere solo poli e zeri del primo o del secondo ordine che si presenteranno in queste forme:
primo ordine:
secondo ordine: 
Per ora limitiamoci ad osservare i termini del 1° ordine.
Per quanto detto,
la F(jw), per quanto riguarda i poli, è il
prodotto di tanti termini del tipo 
oppure 
; queste due forme sono equivalenti perché posso passare da
una all'altra facilmente:
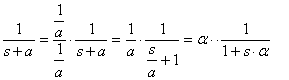
dove a entra nel valore di k.
Fare il prodotto di tanti termini significa fare la somma dei loro logaritmi: graficamente, sul diagramma di Bode, significa che posso sommare i vari grafici corrispondenti ai vari termini elementari per ottenere il grafico della funzione F(s).
Comportamento di un singolo polo
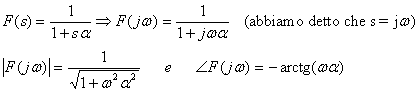
Graficamente possiamo vedere l'andamento del modulo in 6.8.
Guardando la
formula ottenuta per il modulo di F(s), possiamo analizzare il grafico
dividendolo in due zone: se wa << allora |F(jw)| tende
ad 1, cioè a 0 dB se wa
>> 1 allora |F(jw)| tende ad 1/wa; esprimendo questa quantità in dB, otteniamo -[20log(w)+20log(a)] dB.
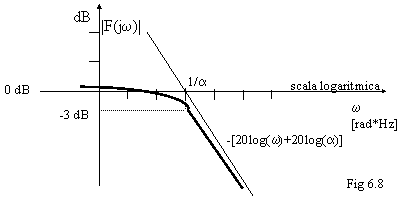
Quindi quando wa >> 1 |F(jw)| = -[20log(w)+20log(a)], relazione che può essere vista come una retta del tipo:
y=-x+c che incontra l'asse y=0 dB quando w a
La pendenza della retta a cui tende asintoticamente il modulo è di 20dB/decade
In definitiva l'unico valore veramente interessante è a, perchè così sappiamo dove posizionare la curva; a lo si legge direttamente in F(s).
Comportamento di un singolo zero
In relazione al grafico in .6.10,
possiamo come prima individuare in due zone: Se wb << allora |F(jw)| tende
ad 1, cioè a 0 dB Se wb
>> 1 allora |F(jw)| tende ad wb, che espresso in dB è pari a [20log(w)+20log(b)] dB.
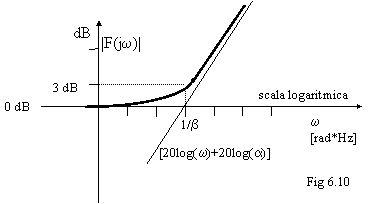
Quindi |F(jw)| tende asintoticamente alla retta [20log(w)+20log(b)] dB che incontra l'asse y=0 dB quando w b
La pendenza della retta è 20dB/decade.
Anche in questo caso l'unico valore intressante è b, perchè così sappiamo dove posizionare la curva; b lo si trova direttamente in F(s).
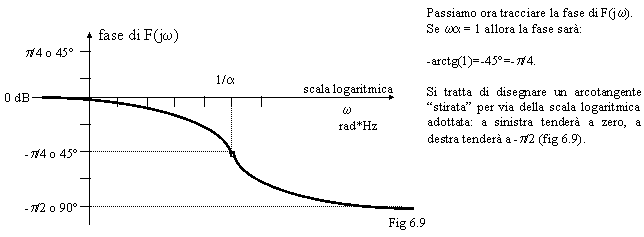
Vediamo ora l'andamento della fase in 6.11.
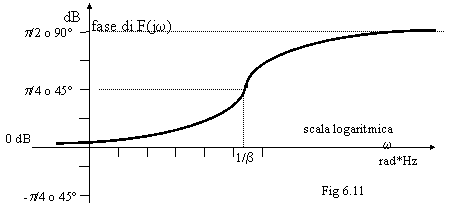
Come accennato prima, siccome F(s) è il prodotto di molti termini, graficamente F(s) può essere ottenuta sommando i grafici ottenuti dai singoli termini. L'importante è che ogni grafico elementare sia posizionato in modo opportuno.
Vediamo due casi particolari:
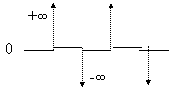
- zero nell'origine: F(s)=ks 
- polo nell'origine: F(s)=k/s 
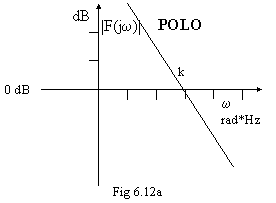
Non possiamo posizionare un polo o un zero nello "ZERO" del diagramma di Bode, perchè dovremmo disegnarlo a - ; ma ciò significa che qualunque frequenza noi scegliamo, sarà sempre molto più grande della frequenza a cui si trova il polo o lo zero. Graficamente, quindi, disegnamo solo la parte asintotica del grafico. In . 6.12a è rappresentato l'andamento di F(s)=ks, in 6.12b è rappresentato l'andamento di F(s)=k/s.
Vediamo ora l'esempio di uno zero e di un polo:
Con
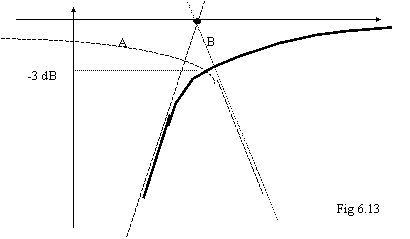
riferimento alla 6.13, il contributo dello zero nell'origine consiste nella
retta B di pendenza 20dB/decade che taglia l'asse X in (1/RC); il contributo
del polo in -l/RC consiste nella curva A. Il risultato di questi due contributi consiste nella curva segnata in grassetto.
 |
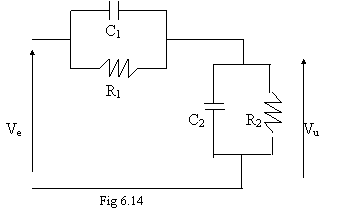
Lo schema del partitore compensato è
presentato in . 6.14. Calcoliamo la funzione di trasferimento.
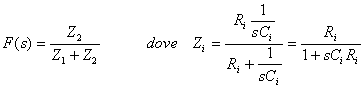
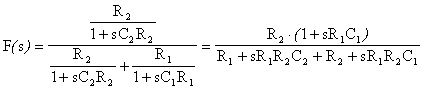
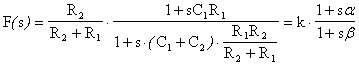
Possiamo ora analizzare la posizione relativa del polo rispetto allo zero; si presentano due casi:
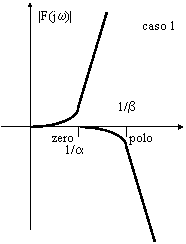
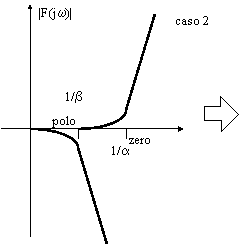
Le curve disegnate sono puramente qualitative; occorre stabilire con maggior precisione la loro altezza e la loro ampiezza.
Possiamo vedere che in continua (frequenza zero) i condensatori scompaiono, viceversa a frequenza infinita se il contributo delle resistenze:
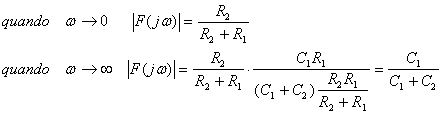
La posizione relativa dello zero rispetto al polo dipende da quale delle seguenti disuguaglianze è vera:
zero a sinistra del polo
2 - 
zero a
destra del polo
3 - 
; sotto questa condizione il polo e lo zero coincidono e il
comportamento del partitore diventa indifferente alla frequenza.
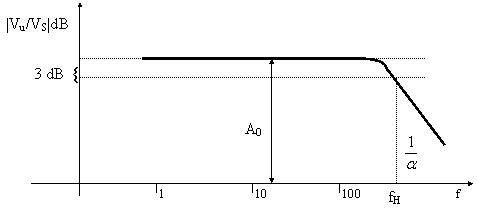
Analizziamo la curva di risposta di un amplificatore a larga banda (untuned) rappresentata in . 6.15.
Se, per semplicità, assumiamo che le 2 rette abbiano pendenza 20dB/decade, la f.d.t. sarà:
fL=a fH=1/a
dove A0, se espresso in dB, è pari all'altezza della zona piatto del diagramma.
Dal grafico possiamo notare che tutte le frequenze centrali sono trattate allo stessso modo mentre all'inizio ed alla fine il guadagno tende a diminuire (diminuisce di un fattore 10 ogni volta che la frequenza aumenta/diminuisce di un fattore 10). Individuiamo 2 frequenze: fL e fH dette frequenze di taglio, frequenze a cui il guadagno è sceso di 3dB rispetto ad A0 e dove la fase è in anticipo o ritardo di 45° rispetto alla banda passante. Nota: frequenza di taglio non vuol dire che tutte le frequenze maggiori o minori vengono eliminate, ma solo attenuate.
Un amplificatore per essere non selettivo (untuned) deve avere la banda passante maggiore od uguale a 3 decadi; se la banda passante è più stretta non posso parlare di amplificatore non selettivo. Se la banda passante è strettissima ho un amplificatore selettivo.
Se mi limito guardare la zona piatta posso dire che il guadagno è indipendente dalla frequenza, cioè l'amplificatore in questa zona di frequenza si comporta come una rete puramente resistiva, cioè che non contiene condensatori (né induttori) che tagliano le frequenze basse e alte. Per capire meglio possiamo dividere idealmente il diagramma e la funzione F(s) in due parti, la parte alle basse frequenze (L) e la parte alle alte frequenze (H):
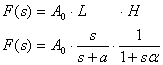
alle basse frequenze avremo:
oppure,
più in generale:
Questa funzione rappresenta il comportamento alle basse frequenze; quando s FL(s) tende ad A0 (per questo motivo numeratore e denominatore devono avere lo stesso grado).
alle alte frequenze avremo:
oppure, più in
generale:
Questa funzione rappresenta il comportamento alle alte frequenze; quando s 0 FH(s) tende a A0 (inoltre deve essere m<n ossia il numero di zeri inferiore al numero di poli, afficnché, quando s , FH (s) tenda a 0, cioè dB).
Da un punto di vista circuitale, alle basse frequenze l'effetto dei condensatori provoca un'attenuazione dell'amplificazione; questa attenuazione va diminuendo al crescere della frequenza, e ciò significa che quei condensatori tendono a comportarsi come corto circuiti, quindi tendono a "sire" dalla rete. A frequenze superiori a fL non hanno più influenza. Analogo discorso per le alte frequenze, dove i condensatori esercitano la loro influenza attenuando l'amplificazione; se si scende verso frequenze più basse questi condensatori tendono a comportarsi come circuiti aperti, quindi tendono a "sire" dalla rete (si potebbero rifare le stesse considerazioni per gli induttori).
Vediamo ora un amplificatore senza frequenza di taglio inferiore:
La curva di risposta rappresentata in . 2.16 è quella degli amplificatori operazionali detti anchi amplificatori per continua.
6.16
A questo punto è possibile analizzare il comportamento di un amplificatore che presenta in ingresso un segnale periodico; in particolare vogliamo calcolare modulo e fase della funzione di trasferimento (nella realtà gli amplificatori servono anche per segnali non periodici, ma a noi basta vedere un esempio).
|
|
Un qualunque segnale periodico può essere sviluppato in serie di Fourier secondo la formula riportata qui a sinistra. Il primo termine della serie è detto armonica fondamentale, mentre i termini successivi sono detti semplicemente armoniche. |
Ricordiamo ancora 2 definizioni:
- se f(t)=f(-t) allora la funzione si dice pari (es. coseno)
- se f(t)=-f(-t) allora la funzione si dice dispari (es. seno)
Lo sviluppo di una funzione periodica pari conterrà solo coseni mentre lo sviluppo una funzione periodica dispari conterrà solo seni.
Vediamo cosa succede se una funzione f(t) come quella appena descritta entra all'interno di uno "scatolo" con f.d.t. classica (ossia banda passante e frequenze di taglio sia inferiore che superiore).
Chiaramente ciò che esce non sarà uguale a ciò che entra, perché ci saranno armoniche (cioè frequenze) che verranno trattate (cioè amplificate) in modo diverso dalle altre; questo significa che avremo sempre distorsione in frequenza (cioè non fedeltà di trasferimento del segnale).
Supponiamo di avere in ingresso un'onda quadra:
e supponiamo di mandarla in una rete con
un solo polo
; quelle armoniche con frequenza elevata saranno
attenuate, mentre le armoniche a bassa frequenza saranno mantenute.
Se derivo l'onda quadra ottengo:
Se derivo lo sviluppo di Fourier (supponendo per semplicità di avere solo termini seno) ottengo:
Analizzando la derivata possiamo osservare che:
- w è la pulsazione quindi è fissa e non posso modificarla
- il coseno è una quantità limitata tra -l ed 1
- bi per definizione di integrale definito è un numero finito
Derivando l'onda quadra ottengo valori infiniti, ma derivando la rispettiva serie di Fourier non riesco a ottenere quantità infinite, a meno di non considerare i termini con i molto grande (i ), cioè le armoniche ad alta frequenza; ma sono proprio queste le armoniche attenuate dal polo, quindi in uscita non riesco ad avere i fronti ripidi.
Quindi le armoniche ad alte frequenze costituiscono i fronti mentre le armoniche di bassa frequenza costituiscono i livelli.Se taglio le basse frequenze significa che taglio i livelli. Se tengo solo le armoniche alte passsano solo i fronti.
In conclusione, per ottenere un'onda quadra anche in uscita devo far passare almeno una decina di armoniche oltre alla fondamentale.
Se è presente la fL sicuramente non passa la componente continua, cioè l'armonica a frequenza zero.
Inoltre, nota che qualunque amplificatore reale ha sempre una frequenza di taglio superiore, cioè aumentando la frequenza, prima o poi, inizia ad attenuare il segnale (circuitalmente è sempre presente un condensatore verso massa).
Per ottenere una ben determinata curva di risposta dobbiamo essere in grado di inserire poli e zeri ha nostro piacimento in modo da modellare la curva di risposta.
Introduzione di un polo del 1° ordine
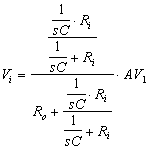
Come
rappresentato in ura 6.17, introduciamo un polo aggiungendo un
condensatore in parallelo al
segnale; infatti:
[
]
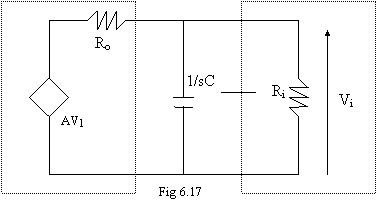
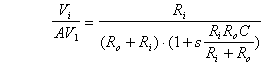Introduzione di uno zero nell'origine
[
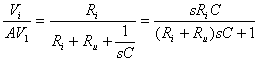zero nell'origine,
polo in 
]
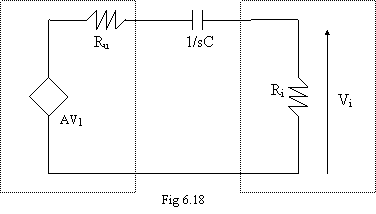
Metto un condensatore in serie al segnale che impedisce il passaggio di frequenze basse ( 6.18). Se metto uno zero nell'origine, a basse frequenze il modulo della funzione di trasferimento si abbassa molto.
Questo è uno dei metodi più semplici per accoppiaree 2 stadi separandoli dal punto di vista della polarizzazione.
Sono disaccoppiati in continua o accoppiati in alternata.
Per avere un polo e uno zero, quindi per realizzare l'amplificatore ad ampia banda, devo avere 2 condensatori, uno in parallelo e uno in serie al segnale, ma con costanti di tempo diverse: una deve essere almeno a 3 decadi dall'altra (condizione minima per parlare di larga banda).
Consideriamo il circuito di 6.19.
6.19
L'impededenza vista dallo stadio di sinistra è:
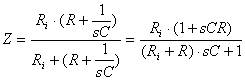
Nota : se s 0 allora Z Ri ( il condensatore diventa un circuito aperto); se s allora Z R//Ri (il condensatore diventa un corto circuito).
A questo punto calcoliamo la f.d.t.:
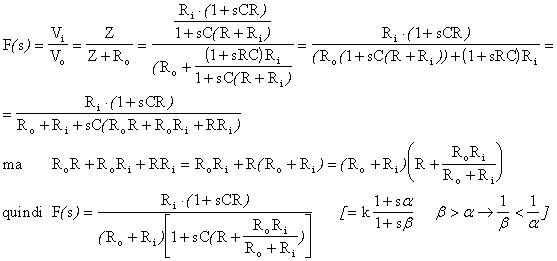
Considerazioni:
lo zero dipende solo da R e da C (vedi numeratore)
il polo dipende da R, Ri, Ro e da C
la frequenza del polo è più bassa di quella dello zero ( 6.20)
6.20
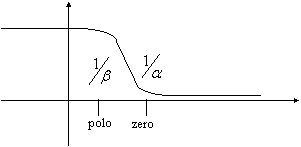
il valore dello zero lo posso decidere variando R e C
con la coppia resistore-condensatore inserisco un polo ed uno zero con il polo a frequenza più bassa
utili per fare compensazione zero-polo
per fare un polo a basse frequenze (ordine dell'Hz) sarà necessario avere R dell'ordine del MW e C dell'ordine dei mF, cioè resistenze e condensatori di valore molto alto, ma questi valori sono incompatibili con le tecniche di integrazione dei componenti; il trucco consiste nel'ottenere una apparente capacità elevata, sfruttando l'effetto Miller.
Sia data una rete N con due punti A e B collegati tramite un' impedenza Z:
. 6.21
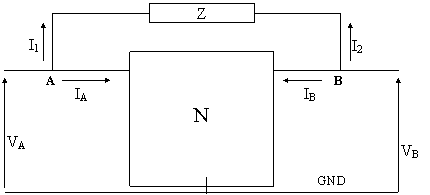
Vediamo sotto quali condizioni il circuito di . 6.21 è equivalente al circuito di 6.22:
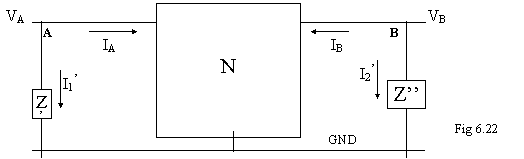
Determiniamo quale legame sussiste tra le impedenze della seconda rete e l'impedenza della prima. Innanzitutto i due circuiti sono equivalenti se le tensioni e le correnti di ingresso/uscita della rete N sono uguali; questo implica che I1=I1' e che I2=I2':
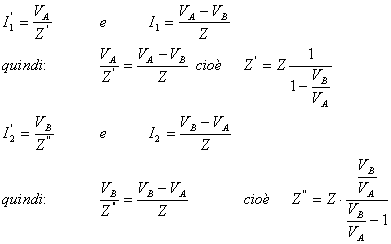
Concentriamoci sull'espressione trovata per Z' :
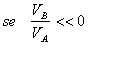
otteniamo un valore di Z' molto piccolo (impedenza di ingresso del secondo circuito molto piccola); se Z è un condensatore, chiamando G=-(VB/VA), otteniamo:
Così si vede chiaramente che se G è molto grande, l'impedenza di ingresso del secondo circuito diventa un condensatore di capacità elevata pari a C(1+G). Otteniamo in tal modo che il condensatore visto all'ingresso è molto più grande di quello collegato fisicamente; tale trucco si utilizza in tecnologia integrata dove non si possono realizzare grandi capacità.
Sfruttando l'effetto Miller è possibile introdurre dei poli a basse frequenze; infatti, come visto prima, valori alti di capacità implicano alti valori delle costante di tempo e quindi poli molto vicini all'origine.
Questo condensatore posto in serie
disaccoppia in continua il prossimo stadio.
Consideriamo un generico stadio ( 6.23).
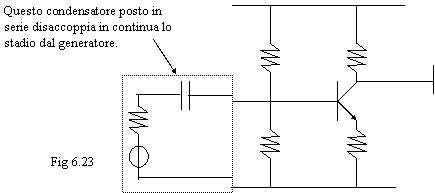
Il punto di funzionamento a riposo non viene influenzato dall'aggiunta dei condensatori, perché questi, per quanto riguarda la polarizzazione, si comportano come circuiti aperti. Se invece accoppio direttamente un generatore e/o un altro stadio, il punto di funzionamento cambia, perché tiene conto della presenza del generatore, della sua resistenza interna e della presenza dell'altro stadio ( 6.24).
6.24
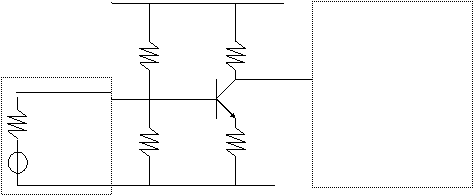
Utilizzare i condensatori in questo modo è molto utile per disaccoppiare in continua gli stadi; ma questa tecnica taglia la continua, cioè il segnale a frequenza zero, e quindi non va bene se si vuole che questo non accada.
Riprendiamo lo stadio appena visto, ma un po' semplificato ( 6.25).
All'interno
della maglia troviamo la Veq del segnale ma anche la VBE
del transistore; quest'ultima tensione è uno dei tre parametri principali
di un transistore bipolare che subiscono l'influenza della temperatura: La VBE (25 mV
/ °C) Il b (1% / °C) La ICB raddoppia ogni 10°C (corrente di saturazione
inversa)
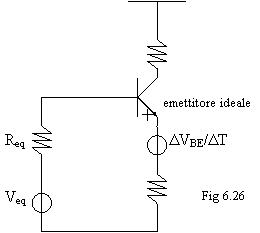
Le variazioni di temperatura inducono variazioni nella tensione VBE , variazioni che modificano il punto di funzionamento a riposo e sono indistinguibili dalle variazioni indotte dal generatore Veq. Possiamo infatti rappresentare le variazioni indotte dalla temperatura con un generatore di tensione posto in serie all'emettitore e supporre ideale l'emettitore ( 6.26).
Come posso separare le variazioni indotte dalla temperatura da quelle indotte dal generatore Veq?
La variazione della VBE rispetto alla temperatura è un fenomeno lento (< 1Hz). Una soluzione poterebbe essere quella di inserire una frequenza di taglio inferiore in modo tale da attenuare fortemente i segnali a bassa frequenza, e quindi quelli dovuti alla temperatura.
Se non è possibile mettere la frequenza di taglio inferiore (ossia il segnale che serve ha anche frequenze lente), per esempio nel caso si debba misurare una temperatura, la nostra unica speranza è separare i due segnali in ampiezza; ma questa soluzione non va bene perché le ampiezze dei due segnali sono del tutto paragonabili (entrambe molto piccole).
Conclusione:
con un solo transistore non riesco a risolvere il problema di amplificare i
segnali che contengono anche basse frequenze. La soluzione
consiste nel mettere nella maglia qualcosa che si opponga all'effetto
termico e lo compensi. Facciamo una modifica circuitale dove nella maglia
sono presenti 2 elementi che si comportano allo stesso modo ma che
circuitalmente sono connessi in modo tale da annullare i loro effetti:
vediamo lo stadio differenziale.
E' quella conurazione che serve per amplificare con basse derive, ed è in grado di amplificare anche la continua.. Ha avuto un notevole sviluppo con i circuiti integrati perchè prima si avevano costi elevati.
Questo stadio
si basa sulla bontà dei 3 elementi che lo costituiscono: - 2 transistori "uguali" (il più possibile) - 1 generatore di corrente con
elevata impedenza in uscita In riferimento alla . 6.27: I0 è un generatore ideale di tensione (eroga corrente
costante indipendentemente dalla tensione presente ai suoi capi) V1, V2 generatori ideali di tensioni (non c'è
la resistenza in serie) La tensione VEE è negativa perché il transisitore è
fatto con transistori e deve funzionare anche con segnale nullo Lo stadio è polarizzato in
corrente (I0)
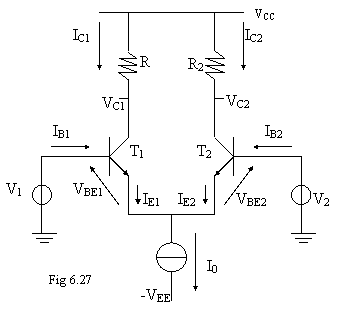
Nell'ipotesi di transistori idealmente identici, abbiamo che IE1 = IE2
Se V1 e V2 sono nulli oppure se V1 = V2 in ogni ramo ho una corrente pari a I0/2.
Scriviamo l'equazione alla maglia riportata in . 6.28.
(1)
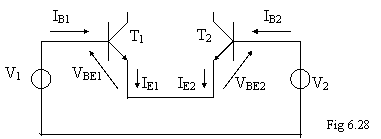
Siccome abbiamo supposto identici i due transistori, le variazioni di VBE1 dovute alla temperatura sono identiche alle variazioni di VBE2 , ma quest'ultime hanno segno opposto, quindi gli effetti dovuti alla temperatura si annullano. In realtà, succede che tanto più i 2 transistori sono uguali tanto più l'effetto di compensazione è marcato.
Facciamo ora l'equazione al nodo riportato in 6.29.
|
|
|
Se le tensioni V1 e V2 non sono uguali la corrente non si divide più in modo uguale sui 2 rami; studiamo il legame tra la Vd e le correnti. Riprendiamo la (2):
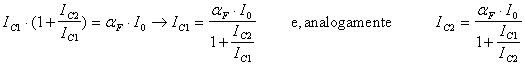
dalla (3), siccome IC=aFIE , otteniamo:
Combinando queste ultime equazioni con quelle trovate poco sopra otteniamo:
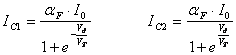
L'andamento delle 2 correnti in funzione della tensione differenziale è rappresentato in . 6.30.
6.30
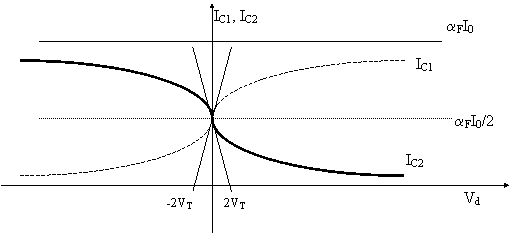
Osservazioni:
Se V1 >> V2 allora tutta la corrente è IC1 (tutta la corrente passa nel ramo sinistro)
Se V2 >> V1 allora tutta la corrente è IC2 (tutta la corrente passa nel ramo destro)
Questo è un comportamento binario dello stadio differenziale che infatti viene sfruttato dalle porte ECL.
A questo punto se R1= R2= RC abbiamo:
se aumento V1 (ossia aumenta Vd) avrò:
Andiamo ora a studiare il tutto per il piccolo segnale; per fare ciò dobbiamo prendere un punto di funzionamento a riposo P, fare la derivata della funzione e calcolarla in P. Sostituiamo così alla curva le tangenti alla curva nel punto P; come punto di funzionamento a riposo prendiamo il punto in Vd=0, sul grafico il punto (0,aFIO/2)
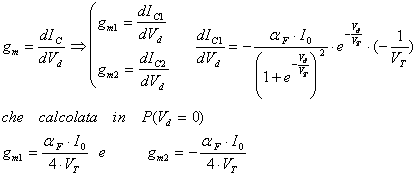
I due valori ottenuti sono i coefficienti angolari delle due rette tangenti che linearizzano lo stadio; scriviamo l'equazioni complete di tali tangenti:
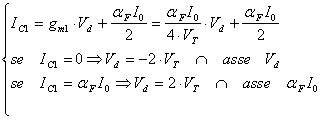
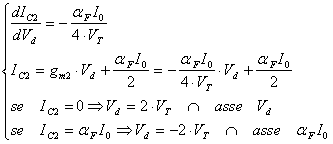
In base alle considerazioni svolte, otteniamo il grafico in 6.31.
6.31
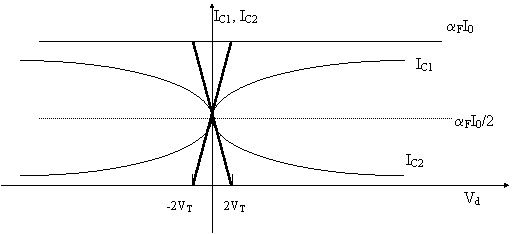
Ora è possibile calcolare l'errore relativo, nel punto Vd=VT, causato dalla sostituzione della curva con la retta tangente passante per P:
L'errore che si commette è pari a 2/75, cioè circa il 2,6 %.
Definizione di deriva: scostamento di una certa grandezza in funzione di un'altra; si tratta di un effetto dinamico, per esempio la variazione della tensione rispetto alla variazione della temperatura.
Definizione di offset: scostamento costante di una certa grandezza rispetto ad un valore di riferimento; si tratta di un effetto statico, ad esempio la differenza di tensione tra due generatori che dovrebbero essere uguali.
Nel caso dello stadio differenziale, se il transistor T1 e il transitor T2 non sono perfettamente uguali, le due correnti IE1 e IE2 , anche con V1=V2=0, sono diverse e quindi ho un offset di corrente.
Le derive possono essere viste come variazioni di offset rispetto a una certa grandezza; per esempio le due tensioni VBE1 e VBE2 sono diverse (offset di tensione) e variano con il variare della temperatura (deriva).
L'offset è recuperabile perchè una volta che è noto lo posso compensare con un generatore di segno opposto:
|
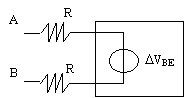
| A e B sono i due ingressi dello stadio differenziale; DVBE o VOFF rappresenta lo scostamento tra VBE1 e VBE2. |
Per quanto riguarda le correnti, per studiare l'effetto delle derive e degli offset occorre riprendere il circuito dello stadio differenziale aggiungendo però le resistenze in serie ai generatori V1 e V2; poniamo per semplicità che V1=V2=0 e quindi nel disegno di 6.32 sono ssi i due generatori.
6.32
Scriviamo l'equazione alla maglia:
Nell'ipotesi di idealità, IB1 = IB2 e VBE1 = VBE2 quindi, affinché l'equazione sia vera, deve essere RB1 = RB2. Questo significa che per limitare gli offset, le due resistenze poste agli ingressi devono essere il più possibile uguali.
Nell'ipotesi realistica che i due transitori siano leggermente diversi, avrò che IB1 IB2 e dunque, pur avendo RB1 = RB2 non riesco ad eliminare l'asimmetria. Per ottenere questo risultato dovrei eliminare le resistenze, ma siccome questo non è praticamente possibile, cerco di mettere le resistenze più piccole possibili. In questo modo
IB1 RB1 IB2RB2 diventa trascurabile rispetto a VBE1 VBE2 e posso considerare come unico offset significativo quest'ultimo:
Quindi agli ingressi metto due resistenze uguali e molto piccole.
CAPITOLO 6
SOMMARIO
6.1. Funzioni di trasferimento, modulo e fase..
6.1.1 Andamento del modulo e della fase in funzione di w (o di f).
6.1.2 Tracciamento del modulo e della fase.
6.2. Un esempio importante: il partitore compensato.
6.3. Curve di risposta degli amplificatori.
6.4. Introduzione di poli e zeri..
6.5. Effetto Miller..
6.6. Esempio di disaccoppiamento in continua
6.7. Effetti della temperatura (cenni)
6.8. Stadio differenziale
6.9. Derive e offset: prime considerazioni
|
Privacy
|
© ePerTutti.com : tutti i diritti riservati
:::::
Condizioni Generali - Invia - Contatta
