Relazione di Chimica

LE LEGGI DEI GAS

Mercoledì 15/12/04, presso il laboratorio di fisica della scuola Federico II di Apricena, abbiamo effettuato due esperienze per verificare due importanti leggi dei gas: la legge di Charles e la legge di Boyle. Per entrambi gli esperimenti è stata presa l'aria come gas su cui effettuare le esperienze.

LA LEGGE DI CHARLES

Obiettivo: verificare la legge di Charles (o isobara)

Strumenti e materiali: due basi con asta, morsetti, pinze, siringa di plastica da 60 ml (raggio 14.4 mm), tappi di gomma, termometro, becco bunsen, acqua di rubinetto, aria.

Per verificare la legge di Charles, legge riguardante i gas a pressione costante, perciò detta isobara, la quale dice che l'aumento di temperatura di un gas è direttamente proporzionale al suo volume, abbiamo preso due basi con asta metallica e applicato ad entrambe un morsetto, abbiamo inserito poi in entrambi i morsetti un'altra asta metallica e ad entrambe queste abbiamo applicato una pinza. Abbiamo preso una siringa da 60 ml e con un calibro ne abbiamo misurato il diametro (28.8mm) e quindi il raggio. Poi con un tappo di gomma, dopo aver tirato il pistone fino a 30 ml per far entrare l'aria, abbiamo chiuso l'estremità della siringa e l'abbiamo inserita in una delle due pinze. Lo stesso abbiamo fatto con un termometro con la differenza che il tappo lo abbiamo fatto scorrere fino alla metà dello stesso in modo tale che la pinza dove poi è stato inserito stringesse il tappo e non direttamente il termometro che altrimenti si sarebbe rotto. Abbiamo posizionato un bicchiere sotto la siringa  e al suo interno, oltre alla siringa stessa, abbiamo inserito anche il termometro e vi abbiamo versato 500 ml di acqua di rubinetto a temperatura ambiente e, dopo aver misurato la temperatura che era 19°C, abbiamo potuto constatare che il pistone non si era mosso: il volume dell'aria all'interno della siringa non era cambiato e il pistone si trovava, come all'inizio, ad una altezza di 55 mm, altezza misurata con una striscia di carta millimetrata incollata alla siringa stessa. Successivamente abbiamo versato nello stesso bicchiere 500 ml di acqua calda. Dopo aver misurato la temperatura, che era salita a 34°C, abbiamo osservato il pistone che si era portato ad una altezza pari a 56 mm, in quanto il volume dell'aria era aumentato. Poi abbiamo messo la siringa e il termometro in 1 l di acqua calda a 50.5°C e abbiamo osservato nuovamente il pistone che apparentemente non si era mosso, ma che, come abbiamo potuto vedere sviluppando i calcoli di seguito riportati, in realtà si era portato ad una altezza di 56.26 mm. Dopo aver effettuato questa rivelazione il tecnico ha riscaldato un altro litro d'acqua sul becco bunsen e ha immerso al suo interno nuovamente la siringa e il termometro che ha misurato una temperatura di 86°C. Questa volta il movimento del pistone si era potuto osservare in quanto è stato di molto maggiore a quelli precedenti, infatti si era portato ad una altezza di 64,2 mm quindi il volume dell'aria all'interno della siringa ha avuto una grossa dilatazione. Tutto quanto detto fin ora può essere riassunto nella seguente tabella completata con il volume dell'aria in mm³ e in l ottenuti sviluppando i calcoli algebrici riportati in seguito e la temperatura espressa in Kelvin ottenuta sommando 273 ai valori in °C.

Svolgimento dei calcoli

Per lo svolgimento dei calcoli abbiamo innanzitutto calcolato l'area di base della siringa, che essendo un cerchio si calcola con la formula A = π ^. r² :

r = 14,4 mm

A_b = (14.4 mm)^{2 .} 3.14 = 651 mm²

Poi per calcolare il volume in mm³ abbiamo applicato la formula del volume del cilindro, essendo la siringa un cilindro, appunto. V = Ab ^. h, dove h indica l'altezza raggiunta dal pistone:

V₁ = 651 mm^{2 .} 55 mm = 35805 mm³

V₂ = 651 mm^{2 .} 56 mm = 36456 mm³

V₃ = 651 mm^{2 .} 56.26 mm = 36625 mm³

V₄ = 651 mm^{2 .} 64.2 mm = 41794 mm³

Effettuando poi l'equivalenza tra mm³ e dm³ e poi tra dm³ e l otteniamo i valori del volume espressi in l che sono stati riportati in tabella.

Rappresentando i valori della temperatura in K e il volume in l sul piano sectiunesiano, i punti definiscono una linea quasi retta, questo perché i valori del volume sono direttamente proporzionali a quelli della temperatura, come è detto nella legge stessa e come si può vedere dai calcoli. La linea non è perfettamente retta perché, come in qualsiasi esperimento, sono presenti degli errori sistematici e accidentali che hanno influito sui valori delle misure ed è inoltre impossibile effettuare l'estrapolazione.

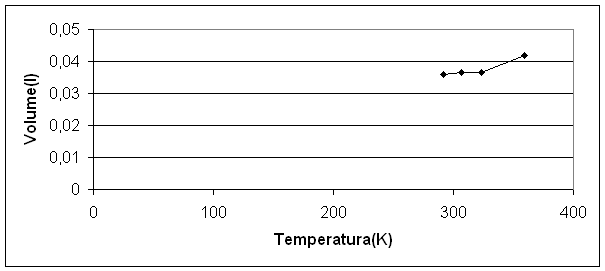
Calcolando i valori che dovevamo ottenere realmente tramite l'equazione V₁/T₁=V₂/T₂, da cui si ricava la formula V₂= V₁^.T₂/T₁  e rappresentandoli sul grafico otteniamo invece una linea retta:

V₁ = (0.0358 l ^. 292 K)   / 292 K = 0.0358 l

V₂ = (0.0358 l ^. 307 K)   / 292 K = 0.0376 l

V₃ = (0.0358 l ^. 323.5 K) / 292 K = 0.0396 l

V₄ = (0.0358 l ^. 359 K)   / 292 K = 0.0440 l

Quindi otteniamo la seguente tabella i cui valori sono riportati nel grafico:

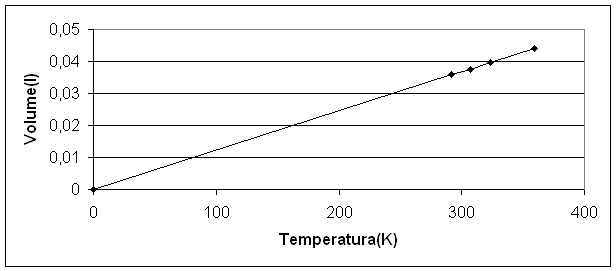
Grazie a questo grafico è possibile dimostrare come tra le grandezze volume e temperatura ci sia un rapporto di proporzionalità diretta. Effettuando l'estrapolazione grafica si può vedere anche come la retta intersechi l'asse delle temperature nel valore 0 e come questo corrisponda al valore 0 del volume: ad una temperatura di 0 K (che viene detta zero assoluto) il volume assume un valore nullo.

LA LEGGE DI BOYLE

Obiettivo: verificare la legge di Boyle (o isoterma)

Strumenti e materiali: una siringa di plastica da 60 ml (raggio 14.4mm); base con asta metallica, morsetto, pinza, tappo di gomma, mattoncini di marmo (di peso superiore al kg), aria.

Per verificare la legge di Boyle, legge riguardante i gas a temperatura costante, perciò detta isoterma, la quale dice che il volume di un qualsiasi gas ideale che si trova a temperatura costante è inversamente proporzionale alla pressione, abbiamo preso la base con asta metallica e vi abbiamo collegato il morsetto. Al morsetto abbiamo collegato un'altra asta metallica alla cui estremità era attaccata una pinza e all'interno di questa abbiamo inserito la siringa con la quale abbiamo aspirato dell'aria tirando il pistone, fino a quando questo non aveva raggiunto un'altezza di 55 mm sulla carta millimetrata che vi era incollata sul fianco. Quindi ad una pressione iniziale di circa 1atm, in quanto Apricena non si trova esattamente a livello del mare, l'altezza del pistone era di 55 mm.

A questo punto, con il tappo di gomma, abbiamo chiuso l'estremità della siringa per non far uscire l'aria e l'abbiamo abbassata fino a quando il tappo è arrivato a toccare la base dell'asta. Successivamente, abbiamo poggiato un mattone di marmo sul pistone della siringa e abbiamo visto che il pistone si è portato da un altezza di 55mm a una di 45mm. Abbiamo poi aggiunto altri 3 mattoni su quello precedente, e il pistone ad ogni mattone si è abbassato,  portandosi a 39, 34 e 30 mm di altezza rilevati con una pressione rispettivamente di 2, 3 e 4 mattoni più quella iniziale di 1atm.

Svolgimento dei calcoli

Effettuando gli opportuni calcoli possiamo sapere il volume dell'aria cui corrispondono i 55, 45, 39, 34 e 30 mm di altezza del pistone.

Siccome la siringa è un cilindro il suo volume si calcola facendo il prodotto tra l'area di base e l'altezza, in questo caso quella del pistone. L'area di base di un cilindro si calcola applicando la formula dell'area del cerchio:

A_b = (14.4 mm)^{2 .} 3.14 = 651 mm²

Quindi l'area di base è pari a 651mm²; moltiplicando questo valore per quello delle varie altezze otteniamo V₀, V₁, V₂, V₃ e V₄, cioè i valori dei volumi in mm³:

V₀ = 651 mm^{2 .} 55 mm = 35805 mm³

V₁ = 651 mm^{2 .} 45 mm = 29295 mm³

V₂ = 651 mm^{2 .} 39 mm = 25389 mm³

V₃ = 651 mm^{2 .} 34 mm = 22134 mm³

V₄ = 651 mm^{2 .} 30 mm = 19530 mm³

Effettuando l'equivalenza tra mm3 e dm3 e tra dm3 e l si ottengono i valori del volume in l riportati nella tabella che segue.

Per calcolare la pressione invece utilizziamo la formula P1= (P₀ ^. V₀)/ V₁ derivante dall'equazione della legge di Boyle P₀^.V₀=P₁^.V₁:

P₀= 1atm

P1= (1atm . 0.035805 l)/ 0.029295 l = 1.22atm

P2= (1atm . 0.035805 l l = 1.41atm

P3= (1atm . 0.035805 l)/ 0.022134 l = 1.62atm

P4= (1atm . 0.035805 l)/ 0.019530 l = 1.84atm

Quanto detto fin ora può essere riassunto nella seguente tabella:

Riportando in ascissa i valori del volume e in ordinata quelli della pressione, è inoltre possibile disegnare il grafico dell'esperimento:

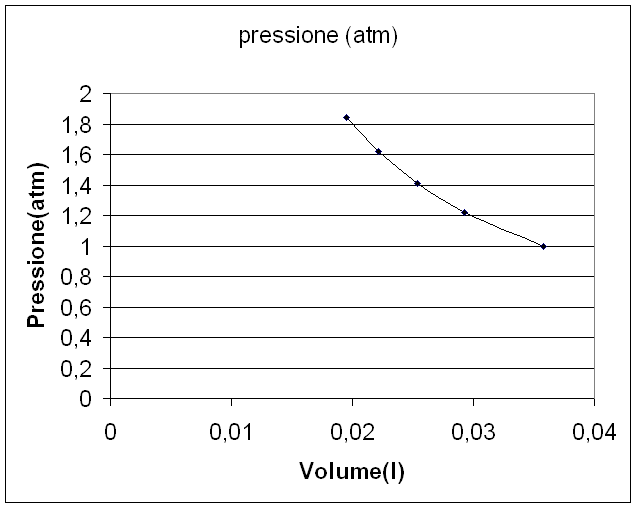
come si può vedere, il grafico risultante è un ramo di iperbole equilatera, questo perché, come è detto nella legge di Boyle e come si può vedere dai risultati dei calcoli, la pressione è inversamente proporzionale al volume , cioè all'aumentare dei valori dell'una , diminuiscono i valori dell'altro.