Interessi semplici: S(1+ki) dove S è il capitale, K sono gli anni e i il tasso d'interesse

Interessi composti: S(1+i)^k

Legge lineare: W(t)=S(1+it)

Legge esponenziale: w(t)=S(i+1)^t

Interesse: si definisce interesse nel periodo da t a t+t l'incremento: DW(t)=W(t+t)-W(t) subito dalla funzione valore nello stesso periodo. Si tratta di una quantità positiva misurata in unità monetarie.

Fattore di capitalizzazione: è il rapporto tra il valore nell'istante finale e quello nell'istante iniziale del periodo. È il fattore per cui va moltiplicato W(t) per ottenere il valore a fine periodo. È una grandezza adimensionale.

Fattore di sconto: è il reciproco del fattore di capitalizzazione: . Moltiplicando il valore W(t+t) per il fattore di sconto si ottiene il valore di inizio periodo. È adimensionale e sempre <1.

Tasso d'interesse: è il rapporto tra l'interesse maturato nel periodo ed il valore nell'istante iniziale: . È adimensionale.

Tasso di sconto: detto anche tasso di interesse anticipato, è il rapporto tra l'interesse ed il valore di fine periodo: . È adimensionale.

Intensità d'interesse:

Intensità di sconto:

Intensità istantanea d'interesse: rappresenta la "sensitività" alle variazioni temporali della funzione valore, espressa in termini di variazione percentuale per unità di tempo, ed in questo senso è anche nota come semielasticità di W rispetto al tempo. È il tasso d'interesse rapportato ad un periodo tendente a 0

Operazione finanziaria: è un qualunque insieme di amenti (in entrata o in uscita), caratterizzato dalle rispettive date di esigibilità. Si potrà dire che l'operazione finanziaria è costituita dal flusso d'importi x sullo scadenzario t. E' naturale definire equivalenti due operazioni finanziarie che differiscono tra loro unicamente per importi di entità pari a 0.

Operazione finanziaria SOMMA: date due operazioni finanziarie, si definisce operazione finanziaria somma l'operazione ottenuta ridefinendo le due operazioni componenti sullo scadenzario unione t e sommando algebricamente i amenti esigibili alle stesse date.

Titoli a cedola nulla: garantiscono, al portatore, il amento, da parte dell'emittente, di una somma di importo fissato C ad una stabilita data futura S. Un titolo di questo tipo, viene alternativamente indicato come "titolo di puro sconto" o "titolo a capitalizzazione integrale" o "zero coupon bond". La durata s-t rappresenta la vita residua o vita a scadenza del titolo. Ex: BOT, tassati al momento dell'acquisto o alle date dei amenti dell'obbligazione, secondo un'aliquota fissa.

Titoli a cedola fissa: questo tipo di titoli garantisce al portatore il amento di un flusso di m amenti periodici; i primi m-l tutti uguali ad un importo fissato I>0 (cedola o coupon) e l'ultimo espresso da C+I essendo C il capitale o valore facciale. Vengono anche detti "coupon bond", "bullet bond" o "straight bond". Il valore facciale C, identifica il valore di parità del titolo. Se il prezzo di acquisto P è uguale a C si dice che il titolo è emesso alla pari. Il rapporto I/C è il tasso cedolare del titolo. Se si sommano le cedole ate in un anno e si divide per C si ottiene il tasso nominale. Ex: BTP ad aliquota fissa ata come ritenuta sulle poste.

Funzione esponenziale come legge di equivalenza finanziaria: fissato un numero reale d>0, per ogni istante di tempo t, la quantità e^dt rappresenta il valore in t di un importo unitario abile al tempo zero. Si caratterizza quindi una legge di scambio in base alla quale una £ abile in zero è equivalente a e^dt £ abili in t W(t)=x₀e^dt. una somma di x_t £ disponibili in t, può essere considerata come il valore capitalizzato W(t) di un importo W(0) disponibile in zero. Una quantità che cresce con la legge esponenziale subisce incrementi percentuali uguali in intervalli di tempo uguali. Mentre i tassi tendono a zero, le intensità, sia d'interesse che di sconto, tendono all'unico valore limite dato dall'intensità istantanea d, indipendente da t.

Valore attuale dell'operazione finanziaria x: considerando il tempo zero come l'istante corrente ed essendo assegnata una legge di valutazione esponenziale con intensità istantanea d'interesse d, il valore attuale W(0;x_k) dell'importo x_k sarà dato da: con k= 1;2;3..m. Si definisce valore attuale dell'operazione finanziaria x, W(0;x), conformemente all'assegnata legge esponenziale, la somma dei valori attuali dei singoli importi componenti: Nelle stesse ipotesi, vale anche per un generico istante t>0

Operazioni eque: l'operazione finanziaria x si dice equa al tempo t, conformemente alla legge esponenziale adottata quando W(t;x)=0. L'equità caratterizza quindi un'operazione di scambio "in equilibrio" nella quale il valore delle somme incassate è pari a quello delle somme ate. E' quindi necessario che almeno uno degli importi componenti x_k abbia segno diverso dagli altri.

Proprietà invariantiva: se un'operazione finanziaria è equa all'istante t secondo una determinata legge esponenziale, lo è in un qualsiasi altro istante.

Proprietà additiva: se due operazioni finanziarie sono eque in un medesimo istante, conformemente ad una stessa legge esponenziale, anche l'operazione finanziaria somma è equa allo stesso istante, secondo la medesima legge.

Proprietà di uniformità nel tempo: se un'operazione finanziaria è equa all'istante t secondo una determinata legge esponenziale, l'operazione avente tutte le scadenze traslate di un intervallo di lunghezza t è equa nell'istante t+t conformemente alla stessa legge.

Proprietà di scindibilità: la somma di due operazioni eque in due istanti diversi secondo la medesima legge esponenziale, è un'operazione finanziaria equa, secondo la stessa legge, in qualsiasi istante. v(t₀;t₂)=v(t₀;t₁)v(t₁;t₂) E' nota come equazione funzionale della scindibilità. Una legge di capitalizzazione scindibile è dunque tale che un'operazione di sconto relativa ad una assegnato intervallo di tempo può essere scomposta in due successive operazioni di sconto, definite suddividendo l'intervallo di attualizzazione in intervalli di tempo contigui v(t;t')=v(t). In una legge uniforme, il fattore di sconto dipende solamente dalla lunghezza dell'intervallo di attualizzazione e non dall'istante iniziale dell'intervallo. La legge  di capitalizzazione esponenziale è l'unica legge uniforme scindibile.

Scomposizione di operazioni finanziarie: è significativo considerare gli importi x_k di segno positivo separatamente da quelli di segno negativo, scomponendo così l'operazione complessiva x/t nella somma di un'operazione finanziaria attiva y/t ed una passiva z/t. naturalmente, se x/t è equa conformemente ad un'assegnata legge esponenziale, le 2 operazioni componenti avranno valore uguale ma di segno contrario. Un'altra scomposizione significativa si ha separando le somme esigibili in date precedenti e successive un certo istante t>0 W(t;x)=M(t;x)+v(t;x) essendo e che saranno definiti rispettivamente valore montante e valore residuo.

Rendita: una rendita è un'operazione finanziaria r costituita da una successione, limitata o illimitata, di amenti positivi periodici, detti RATE o TERMINI della rendita. Ci si riferisce cioè all'operazione consistente nel flusso r delle rate completato con un importo di segno opposto, esigibile in un istante non successivo al amento della prima rata. Nel caso in cui r p considerata iniziare con il amento della prima rata t₀=t₁ si parla di rendita anticipata, se invece è t₀=t₁-l la rendita è detta posticipata; è immediata se t₀=0, ovvero se la data d'inizio coincide con l'istante attuale; se invece t₀=n, la rendita è differita.

Rendite frazionate: sono delle rendite con amento delle rate su periodi più brevi di un anno.

Le operazioni di rendita nell'aspetto dinamico: in senso strettamente terminologico, si parla di un'operazione finanziaria di rendita in senso proprio se si fa riferimento alla parte che effettua l'operazione di investimento ando S per ricevere poi le rate della rendita. Dal punto di vista della controparte si tratta, più precisamente, di un'operazione di rimborso o ammortamento di un debito S, contratto in zero, tramite il amento di un numero di rate di importo prefissato. I due punti di vista sono equivalenti, a patto di contabilizzare adeguatamente.

Ammortamento a rate costanti posticipate (o francese): si tratta, in pratica, di una rendita posticipata a rate costanti; il debito residuo è espresso, anziché in funzione della situazione debitoria dell'anno precedente, in termini propsettivi, cioè come valore scontato delle rate future, e quindi come reciproco del valore residuo V_k dell'operazione.

Ammortamento a rate costanti anticipate (o tedesco): come per il precedente, si tratta di ricavare un prospetto che ricalchi le relazioni correnti ricavate per le rendite anticipate a rata costante. Il metodo di sviluppo si può basare sulla proprietà M_k=(M_k-l-R)(1+i) che permette di calcolare i successivi valori del debito residuo. La differenza sostanziale col caso precedente, è che ora, la quota di interesse verrà convenzionalmente portata sulla riga del debito residuo dalla quale è ottenuta, per indicare che in questo caso è ata all'inizio dell'anno di competenza.

Ammortamento a quote capitali costanti: lo schema di sviluppo non differisce dall'ammortamento francese, se non per il fatto che tutte le quote capitale sono fissate uguali a S/m e le rate R_k vengono ottenute sommando tale valore a quello delle quote interesse via via calcolate.

Piani con preammortamento: all'interno dell'operazione di ammortamento si può prevedere un periodo di preammortamento, stabilendo di differire di n anni la data di inizio del rimborso del debito. Più precisamente si può convenire che le prime n rate, corrisposte di solito posticipatamente, siano costituite solo dalla quota interesse I_k=iS.

Ammortamento a rimborso unico: è il caso delle operazioni in cui l'importo iniziale S viene restituito in un'unica soluzione col versamento dell'ultima rata, mentre le rate precedenti, posticipate, vengono corrisposte solo a titolo d'interesse. Evidentemente si tratta di un piano con m-l rate di preammortamento, R_k=iS  k=1;2; . m-l ed una sola rata di ammortamento R_m=S+iS.

Piani di ammortamento con periodicità frazionata: i casi con periodicità diversa dall'anno, non presentano novità rispetto a quanto già detto. Si tratterà di contare i tempi frazionati, utilizzando per il calcolo delle quote interesse l'opportuno tasso equivalente.

Tasso interno di rendimento: si definisce TIR di x il tasso d'interesse i^* della legge di sconto esponenziale conformemente alla quale l'operazione finanziaria risulta equa. . L'equazione del TIR è un'equazione algebrica di grado t_k nell'incognita v. In generale, un'equazione del genere ammette fino a t_k radici reali distinte.

Teorema di sectiunesio: Sia N il numero delle variazioni nella successione  dei segni dei coefficenti di p_m(v) e sia h il numero delle radici positive di p_m(v)=0. Allora N-h è un numero pari positivo o nullo. Condizione sufficiente affinchè l'equazione del TIR ammetta un'unica soluzione v^* positiva è che gli importi x₀;x₁;..;x_n cambino segno una sola volta. Dal punto di vista geometrico, l'esistenza e l'unicità della soluzione v^* è garantita dal fatto che la funzione f(v)=Cv^m passa per l'origine, è monotona crescente e continua; il suo grafico intersecherà quindi in un solo punto, di ascissa v^*, la retta y=P. affinchè sia v^*=(P/C)^1/m<1 occorre e basta che sia P/C<1. Si giunge quindi alla ovvia conclusione che, affinchè l'operazione di investimento abbia un tasso di rendimento positivo, è necessario che il prezzo di acquisto P del titolo sia minore del suo valore di rimborso C.

Il metodo di Newton: fissato un valore iniziale v₀ per la variabile incognita, nei metodi a punto unico si calcola, a partire da questo, un nuovo valore v₁, utilizzando un algoritmo v₁=F(v₀) che garantisce che la distanza di v₁ dalla soluzione v^* è minore della distanza di v₀, cioè tale che |v₁-v^*|<|v₀-v^*|. Iterando il procedimento, per le proprietà della funzione F(v) al passo n varranno sempre le diseguaglianze  v^*<v_n+1<v_n con n=1;2 . Quindi, v_n+1=v_n-(f(v_n)-P)/f'(v_n). ripetendo infinitamente la procedura resta quindi individuata comunque una successione decrescente di v_n di approssimazione per eccesso di v^*. Nella pratica basterà fermarsi quando il miglioramento ottenuto nella precisione verrà considerato trascurabile, ovvero quando sarà: v_n-v_n+1<e con e un numero positivo piccolo a piacere.

La funzione di un contratto a pronti:con riferimento al caso più generale di un contratto stipulato in una generica data t, che garantisca con certezza il amento di un'unità monetaria ad una fissata data s successiva, useremo la nozione: v(t;s) con t=<s per indicare il valore al tempo t di una lira esigibile in s. La quantità v(t;s) fissa una regola di equivalenza intertemporale, relativa ad importi a scadenza unitari, tra gli estremi [t;s]. Dato che l'istante in cui l'importo v è determinato e l'istante in cui è considerato esigibile coincidono,  si parlerà di contratto a pronti.

Orizzonte di scambio: è la durata t=s-t. Invece di considerare fissate le date t ed s, il valore v(t;s) può essere pensato come una funzione di due variabili, definita per t ed s, appartenenti ad un opportuno dominio temporale. Al variare di t ed s, la funzione valore v(t;s) dovrà rispettare alcune proprietà formali che ne garantisocno la significatività e la consistenza dal punto di vista economico finanziario:

v(t;s)>0 t=<s NON ARBITRAGGI

v(s;s)=1 spontanea condizione di scadenza

v(t;s')>v(t;s'') t=<s'<s'' postulato del rendimento del denaro, v fissato t è funzione decrescente di s

Quindi, viste la 2 e la 3, v(t;s)<1  t<s

La funzione valore in un contratto a termine: un'importante generalizzazione delle definizioni precedenti si ottiene se si ipotizza che il periodo di scambio abbia inizio in un istante T successivo a t (istante di stipula), secondo lo schema tipico delle operazioni a termine v(t;T;s) con t T s  che sta ad indicare il valore in T, pattuito in t di una lira esigibile in s. Nessun importo monetario viene incassato/versato dai contraenti in data t, nella quale avviene la stipula del contratto; la parte che si impegna ad assumere la posizione di creditore, verserà l'importo v all'istante T, per ricevere, dalla controparte, l'importo unitario a scadenza s. Anche v(t;T;s) dovrà soddisfare le regole che garantiscono la significatività finanziaria:

v(t;T;s)>0    t T s NON ARBITRAGGI

v(t;s;s)=1 t s spontanea condizione di scadenza

v(t;T;s')>v(t;T;s'') con t T s'<s'' o v(t;T';s)<v(t;T'';s) con t T'<T'' s postulato del rendimento del denaro

Almeno dal punto di vista formale, un contratto a pronti è ottenibile come caso particolare nella logica dei contratti a termine, richiedendo che l'istante T di inizio dell'orizzonte di scambio coincida con l'istante t di stipula.

Fattore di sconto e di capitalizzazione: consideriamo i contratti a pronti che garantiscono alla scadenza s un arbitrario importo monetario x_s; indicheremo con: V(t;x_s)=x_sv(t;s) con t s  il valore al tempo ti di x_slire esigibili al tempo s. Usando un'altra denominazione, rappresenta il valore attuale di x_s. Per il principio di indipendenza dall'importo, il valore attuale V si ottiene moltiplicando x_s per la funzione v(t;s) che non dipende da x_s ed è quindi interpretabile come fattore di sconto da t ad s, di conseguenza m(t;s)=1/v(t;s) che rappresenta il valore in s di una lira esigibile in t, determinato secondo la regola contrattuale determinata in t. La funzione m(t;s) fornisce quindi il fattore di capitalizzazione o fattore montante fissato in t per il periodo da t ad s. Per l'indipendenza dall'importo, la funzione v(t;s) e m(t;s) individuano una regola di equivalenza intertemporale applicabile ad importi arbitrari, ovvero una legge di equivalenza finanziaria.

L'ipotesi di consistenza tra contratti a pronti e contratti a termine: all'interno del contratto stipulato in t, il valore in t di una lira abile in s, deve coincidere con il valore v(t;T;s) all'istante T, attualizzato con il fattore di sconto v(t;T); quindi v(t;s)=v(t;T)v(t;T;s) con t T s.

La proprietà di scindibilità: la proprietà di scindibilità precedentemente introdotta, richiede che sia v(t;s)=v(t;T)v(T;s), t T s; la somiglianza con l'espressione scritta poco sopra, è soltanto apparente: affinché le due proprietà coincidano deve essere: v(t;T;s)=v(T;s),t T s; il valore del contratto a termine stipulato in t deve cioè coincidere col vlore nel contratto a pronti stipulato nell'istante "futuro" T.

Tassi ed intensità di interesse su orizzonti di scambio finiti: faremo riferimento alla funzione montante m(t;s) e ne considereremo le variazioni all'interno del contratto stipulato in t. Studieremo cioè il valore m come funzione della sola variabile s, considerando l'istante contrattuale t fissato. Assegnati due istanti di tempo s t ed s'=s+t con t>0, l'interesse realtivo all'orizzonte di scambio [s;s'] è espresso dall'incremento: Dm(t;s))m(t;s+t)-m(t;s). Dividendo l'interesse per il valore calcolato all'inizio del periodo, si ottiene il tasso d'interesse sul periodo [s;s']: j(t;s;s+t)= La dipendenza da tre variabili temporali, evidenzia il fatto che j(t;s;s') ha il significato di un tasso d'interesse a termine, fissato al tempo t ma relativo all'orizzonte di scambio (di sconto/capitalizzazione) [s;s']. Il tasso j può inoltre esssere espresso direttamente a partire dal valore di sconto a termine, secondo la relazione: j(t;s;s+t)= ed inoltre che definisce l'intensità d'interesse a termine fissata in t per l'orizzonte [s;s+t]. Nel caso particolare s = t si ottiene l'espressione del tasso di interesse a pronti: j(t;t+t)=m(t;t+t)-l= e quella dell'intensità di interesse a pronti: g(t;t+t)=

Tassi equivalenti: conviene introdurre il tasso di interesse a termine espresso su base annua, i(t;s;s+t), equivalente al tasso j(t;s;s+t) secondo la legge esponenziale, o, come si usa dire, in regime di interessi composti. La quantità i(t;s;s+t) è definita come il tasso annuo della legge esponenziale che, sull'intervallo da s a s+t produce un montante: (1) m(t;s;s+t)=[1+i(t;s;s+t ^t uguale a quello espresso dal tasso d'interesse j, cioè: (2) m(t;s;s+t)=1+j(t;s;s+t). Dalle due espressioni precedenti, si ricava quindi la relazione tra tassi equivalenti in regime esponenziale: (3) i(t;s;s+t)=[1+j(t;s;s+t ^t-l. In alcune applicazioni è anche usato il tasso d'interesse equivalente in regime di interessi semplici, definito come il tasso annuo i(t;s;s+t), che sull'intervallo sa s a s+t produce un montante secondo la legge di crescita lineare: (4) m(t;s;s+t)=1+i(t;s;s+t t. Uguagliando la (4) e la (2) si ottiene in questo caso l'espressione dei tassi equivalenti in regime lineare: (5) i(t;s;s+t)=. Se il periodo di lunghezza unitaria non è l'anno, le espressioni (3) e (5) forniscono in generale i tassi equivalenti su base periodale, espressi cioè scegliendo come base dei tempi proprio il periodo unitario. Per ottenere, dal tasso j, espresso secondo una base dei tempi assegnata, il tasso equivalente i espresso secondo una nuova base, è sufficiente scegliere una nuova base come unità di tempo ed applicare la (3) oppure la (5), esprimendo t come la lunghezza della vecchia base espressa secondo la nuova scala dei tempi. Il tasso d'interesse j relativo al periodo [s;s+t] può anche essere interpretato come il tasso d'interesse della legge esponenziale che, espressa scegliendo come unità di tempo la durata t, equivale alla funzione montante m(t;s). m(t;s;s+1)=[1+j(t;s;s+1)]¹ Un'analoga osservazione vale nel caso della legge lineare in relazione ai tassi equivalenti in regime di interessi semplici, dato che si può anche scrivere, formalmente: m(t;s;s+1)=1+j(t;s;s+1)*1.

L'intensità istantanea d'interesse: se si ammette che la funzione m(t;s) sia dotata di derivata parziale rispetto alla variabile s, la definizione di intensità di interesse può essere estesa ad orizzonti di scambio di durata infinitesima. Per ogni t s, si definisce intensità istantanea di interesse il limite cui tende l'intensità di interesse g(t;s;s+t) quando l'ampiezza t dell'orizzonte di scambio tende a zero. Si ottiene così la funzione:== Dato che m(t;s) è funzione crescente di s, l'intensità istantanea d'interesse è positiva. Inoltre, per la positività del montante,, può sempre scriversi come derivata logaritmica nella forma: oppure come: . In molte applicazioni si considera spesso sognificativo specificare la forma dei contratti finanziari, scegliendo come punto di partenza la funzione d(t;s). Secondo questo atteggiamento modellistico, la funzione valore v(t;s) sarà: con t s, che costituisce l'espressione in forma integrale del fattore di sconto, data la funzione di intensità istantanea di interesse. Quest'ultima formula, può essere estesa al caso di operazioni a termine: 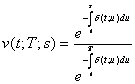con t T s

Leggi uniformi: una funzione di sconto v(t;s), per essere uniforme nel tempo, deve dipendere solo dalla lunghezza t=s-t dell'intervallo di attualizzazione. La stessa proprietà formale vale anche per l'intensità istantanea d'interesse. Deve perciò valere per tutte le funzioni uniformi, la seguente proprietà: d(t;t+t d t) con t 0. Avremo perciò: e quindi:

Leggi scindibili: se il fattore di sconto è dotato della proprietà di scindibilità, dovrà valere la relazione tra contratti a pronti e contratti a termine. Sulla base della funzione intensità istantanea d'interesse applicata alle operazioni a termine, tale relazione sarà espressa con: che dovrà, naturalmente, essere valida per ogni scelta dei tempi t, T ed s (con t T s). Ciò è possibile solo se vale l'uguaglianza d(t;s)=d(T;s) sempre, per ogni terna ordinata di t, T ed s. Ne consegue quindi, che la funzione intensità istantanea di interesse deve essere indipendente dalla variabile t, e cioè: d(t;s)=d(s) con t s. Quest'ultima è una condizione necessaria e sufficiente per la scindibilità, ed è l'equivalente di richiedere che la funzione d venga scelta una sola volta qualunque sia l'istante di stipula del contratto. Da ciò risulta immediato notare, che la legge esponenziale, si conura come l'unica legge uniforme scindibile, soddisfacendo: d(t;s)=d costante e quindi: .

L'intensità di rendimento a scadenza: facendo riferimento ad un contratto a pronti definito da una funzione valore v(t;s), viene definita intensità di rendimento a scadenza (yield to maturity), l'intensità istantanea d'interesse h (costante) della legge esponenziale equivalente sull'orizzonte di scambio [t;s]. il rendimento a scadenza h sarà perciò definito dalla relazione: . Nel caso v(t;s) non esprimesse la legge esponenziale, la costante h muterà al variare di [t;s] e quindi avremo: in cui h rappresenta l'intensità della legge esponenziale fissata in t ed equivalente a v(t;T;s) su [T;s]. Ne consegue che l'intensità di rendimento a scadenza diventerà: ed inoltre: ovvero il rendimento a scadenza come media temporale dell''ntensità istantanea d''nteresse, fissata in t, su [T;s]

Intensità equivalenti: il rendimento a scadenza, pur essendo un'intensità, è, dimensionalmente, un tempo ^-1. Inoltre, dato che h(t;T;s) è, per definizione, l'intensità di una legge esponenziale, risulta che, se si effettua un cambiamento sulla base dei tempi, la nuova intensità di rendimento a scadenza (espressa sulla nuova base ed equivalente alla medesima in base annua, secondo la legge esponenziale) si potrà ottenere, semplicemente moltiplicando h per q (il rapporto tra la lunghezza della nuova e della vecchia base): h'(t';T';s')=h(t;T;s)q. I tempi misurati nella nuova scala saranno dati da t'=t/q. Inoltre, si dovrà avere: . Questa proprietà di linearità rispetto al cambiamento della base dei tempi è valida anche per le intensità di rendimento a scadenza a pronti h(t;s) e per l'intensità istantanea d'interesse d(t;s), di cui le funzioni h rappresentano la media temporale.

La legge di capitalizzazione lineare (sconto razionale): è caratterizzata dal montante lineare: m(t;t+t)=1+kt con k costante positiva. Il corrispondente fattore di sconto ha andamento iperbolico: che è noto come sconto razionale. L'intensità istantanea di interesse ha la forma: che è uniforme (d(t;t+t d t)) ed è decrescente al crescere di t

La legge di capitalizzazione iperbolica (sconto commerciale): consideriamo la legge uniforme di sconto detta commerciale: v(t;t+t)=1-kt t 1/k; essendo k una costante positiva, e limitando i valori di t, per evitare valori non positivi di v. In questo caso, il montante avrà forma iperbolica: e l'intensità istantanea d'interesse: risulterà crescente per i valori di t consentiti. Il tasso di interesse relativo a [t;t+t] è dato da: . Per t=0 si ha: che giustifica l'interpretazione corrente di k come tasso annuo di interesse anticipato.

La linearità del valore attuale: considerando una generica operazione finanziaria x/t non nulla, facendo riferimento all'istante di valutazione t t', potremo indicare con V(t;x) il valore al tempo t (valore attuale) di x/t. Nel caso in cui la funzione valore sia dotata della proprietà additiva avremo: , che, per la teoria dell'indipendenza dall'importo diviene: (funzione lineare). Ne consegue che, la proprietà di linearità del valore attuale, è fornita dall'insieme della proprietà additiva e di quello dell'indipendenza dall'importo.

Valore di un'operazione finanziaria in un istante generico: E' significativo scomporre il flusso x nel flusso x_,T= (tutte le quote abili fino all'istante T) e dal flusso x'_T= (tutti i amenti successivi a T). Dato che le poste di x_,T risultano tutte liquidate all'istante T, il vettore x_,T si può indicare come il flusso liquidato (in T). Sulla base di questa scomposizione, il valore di T del flusso x sarà definito come: . Se t rappresenta l'istante corrente, per T>t la quantità W(T;x) rappresenta un valore ex post, ovvero determinato dai valori delle funzioni di sconto specificate in istanti di tempo tutti successivi a t. La funzione W è anche nota come il reddito prodotto da x in T. La seconda sommatoria, invece, non è altro ceh il valore del flusso residuo in T: La prima sommatoria, invece, definisce un concetto di valore in un istante successivo a quello di esigibilità. Conviene introdurre quindi la definizione di montante di un flusso di importi: . Introdotte queste due definizioni alternative, potremo riscrivere W(T;x) come:. In realtà, la distinzione tra M(T;x_,T) e V(T;x'_T) è una complicazione non necessaria, nel caso della legge esponenziale, in quanto, supponendo che v(t;s)=e^-d(s-t) e T<t_k , il valore di T in x_k è: mentre, per T>t_k, il valore di x_k in T sarà dato da: . Quindi, sia nel caso di valutazione ex ante che di quella ex post, basterà esprimere il valore di x_k in T come:

Equità: considerando un'operazione finanziaria x/t, con legge di sconto v(t;s) sarà sempre possibile avere un'operazione x'/t' aggiungendo alla x/t l'importo x_t=-V(t;x), esigibile al tempo t. L'operazione x'/t' sarà nulla per costituzione: V(t;x')= e si dirà equa in t rispetto alla legge di sconto v(t;s).

Tasso interno di rendimento rispetto ad un valore assegnato: considerando un'operazione x'/t', equa in t secondo i tassi annui d'interesse: i(t;t_k)=v(t;t_k)^-l/(tk-t)-l con k=1,2,3m; si definirà tasso interno di rendimento (TIR) di x'/t' il tasso d'interesse i^* in legge esponenziale, per cui x'/t' risulta equa. i^* dovrà quindi essere tale che:. Sulla base del teorema di sectiunesio, i^* esiste, unico e positivo.

Funzione valore e prezzi di mercato: un titolo obbligazionario è un contratto in cui le parti si impegnano a scambiarsi, quantità di denaro in date diverse. Di solito, tutte le quantità oggetto di scambio sono note con esattezza dalle parti nel momento della sottoscrizione dell'impegno, tuttavia, in alcuni casi, l'ammontare di alcuni importi oggetto di scambio non è conosciuto all'istante si stipula, ma viene determinato successivamente, in base al realizzarsi di alcune condizioni preliminarmente specificate nel contratto. In ogni caso, è determinante la struttura temporale del titolo. Generalmente, i due contraenti possono essere identificati, uno come creditore (long side) ed uno come debitore(short side). Da questo punto di vista, il possesso del titolo funge da garanzia per il creditore da parte del debitore. Il detentore dell'obbligazione può vendere il proprio titolo ad un terzo ad un prezzo concordato, indipendentemente da chi ha emesso la stessa, ed il nuovo acquirente prenderà le parti del vecchio nell'adempimento dell'obbligazione.

Le ipotesi caratteristiche del mercato

non frizionalità: non ci sono costti di transazione né gravami fiscali, i titoli sono infinitamente divisibili, sono consentite le vendite allo scoperto e non c'è rischio d'insolvenza;

competitività: gli agenti del mercato sono massimizzatori di profitto nel senso della "non sazietà" e price takers, cioè non possono influenzare i prezzi;

assenza di arbitraggi: -definizione di arbitraggio: dato x/t non nullo di poste non tutte nulle, essendo t l'istante corrente, con t t₁ t_m x/t è un arbitraggio non rischioso se il flusso x non contiene amenti di segno opposto. Trattasi quindi di una transazione in cui si incassa almeno una volta con la certezza di non are mai. Si distinguono arbitraggi di tipo A [costituiti dall'acquisto, a costo nullo o negativo di un flusso di amenti futuri tutti non negativi, con almeno un amento strettamente positivo: c 0;x_k 0; k=1,2,m, esiste un j tale che x_j>0] e di tipo B [dati da un acquisto di un flusso di amenti futuri, tutti non negativi ad un costo negativo: c<0;x_k 0; k=1,2m.- Assumeremo che sul mercato sia rispettato il principio di non arbitraggio, cioè che sia sistematicamente esclusa la possibilità di effettuare arbitraggi.

Titoli a ceda nulla unitari(ZCB): sono titoli azionari che garantiscono il amento di una lira nell'istante s t. Si tratta di un titolo a cedola nulla dal valore facciale unitario. v(t;s) con t s il prezzo in t del TCN unitario con scadenza s. per evitare arbitraggi non rischiosi, dovrà aversi: v(t;s)>0 con t s; v(s;s)=1. Inoltre bisognerà introdurre come postulato: v(t;s)<1 con t<s, che è detta postulato d'impazienza. Quest'ultimo è necessario per garantire la significatività finanziaria (tassi d'interesse positivi), ma non può essere ricavata come conseguenza necessaria delle ipotesi di mercato.

Teorema di decrescenza rispetto alla scadenza: per evitare arbitraggi, è necessario che sussista: v(t;s')>c(t;s'') con t s'<s''. dimostrazione per assurdo, basata sul fatto che la violazione della proprietà conduce necessariamente alla possibilità di arbitraggi: poniamo v(t;s') v(t;s''). E' allora possibile la presenza di arbitraggi con questa strategia: acquisto in t del TCN con scadenza in s'; vendita allo scoperto in t del TCN con scadenza in s''; acquisto in s' del TCN con scadenza in s''. La composizione delle transazioni porta alla costituzione di un flusso di amenti non nullo e privo di poste negative. La posta 1-v(s';s'') esigibile in s' è strettamente positiva per il postulato d'impazienza, mentre v(t;s'')-v(t;s') abile in t, è non negativa in base all'ipotesi accettata per assurdo. Si tratta quindi di un arbitraggio di tipo A.

Titoli a cedola nulla non unitari: sono TCN che garantiscono alla scadenza s il amento di un importo monetario x_s di ammontare generico, noto nell'istante di valutazione t s. Indicheremo con V(t;x_s) con t s il prezzo in t di questo titolo. Supponendo che sul mercato ci sia la possibilità di infinita divisibilità, sarà possibile creare un portafoglio con una quantità x_s di questi titolo. Visto che il prezzo di un TCN unitario è v(t;s), secondo l'ipotesi che gli agenti siano price takers, il costo facciale dell'intero portafoglio sarà dato da x_sv(t;s). Varrà il seguente:

Teorema dell'indipendenza dall'importo: per evitare arbitraggi deve sussistere l'uguaglianza: V(t;x_s)=x_sv(t;s). Il prezzo in t del TCN con valore facciale x_s e scadenza s dev'essere uguale al prezzo in t del portafoglio contenente x_s unità di TCN con uguale scadenza e valore facciale unitario. Dimostrazione per assurdo: supponiamo che valga V(t;x_s)<x_sv(t;s); sarà allora possibile effettuare u arbitraggio acquistando in t il titolo con valore facciale x_s, vendendo allo scoperto in t x_s TCN unitari con scadenza s. tale strategia garantisce un profitto in t dato dalla differenza positiva di prezzo x_sv(t;s)-V(t;x_s), e la chiusura della posizione scoperta in s; abbiamo quindi un arbitraggio di tipo B. Identica conclusione se valesse la diseguaglianza di senso contrario (inversione dei segni ed adattamento della strategia).

Portafogli di TCN con diversa scadenza: passando a considerare portafogli di titoli elementari, composti da TCN unitari a diverse scadenze, è possibile ricavare relazioni di arbitraggio per titoli obbligazionari complessi, caratterizzati da amenti multipli. Il titolo complesso è qualificabile come un titolo derivato, mentre i TCN unitari possono essere intesi come titoli elementari, o titoli base. Si usa dire anche che il titolo complesso è ridondante.

Teorema di linearità del prezzo: per evitare arbitraggi non rischiosi deve valere: V(t;x)=. Dimostrazione per assurdo: mettiamo sia valida V(t;x)< in questo caso, la strategia che consente l'arbitraggio sarebbe data da: acquisto in t del titolo che garantisce il flusso x/t; vendita allo scoperto in t di x_k TCN unitari con scadenza t_k (un tcn per ogni scadenza). Anche qui si ricava un profitto al tempo t senza contrarre alcun impegno futuro, dato che l'acquisto del titolo complesso garantisce la chiusura di tutte le posizioni scoperte generate dalla vendita di titoli unitari. Si effettua quindi un arbitraggio di tipo B.

Contratti a termine: in generale, un contratto a termine (forward) è una compravendita differita in cui due parti convengono al tempo t, di scambiarsi in una data futura T, ed ad un prezzo prefissato, una determinata quantità di un bene. L'istante T è la data di consegna del bene ed il prezzo da corrispondere è il prezzo a termine (o forward) stabilito in t per consegna in T. Nel nostro mercato, il bene scambiato è costituito da titoli obbligazionari, che, alla data di consegna dovranno avere, evidentemente, una vita residua non nulla: dovranno essere cioè caratterizzati da date di scadenza successive a T. La quantità v(t;T;s) con t T s rappresenta, nell'attuale contesto, il prezzo a termine in t, per consegna in T, di un TCN unitario con scadenza in s. Anche in una logica di mercato è sempre possibile vedere un contratto a pronti stipulato in t come un particolare contratto a termine che abbia T=t. Dovrà quindi valere l'uguaglianza: v(t;t;s)=v(t;s) con t s. l'operazione di scambio a termine è un contratto scritto su un altro contratto, o se si preferisce, è un titolo che implica l'acquisto/vendita di un titolo elementare. Rientra quindi anch'esso nella categoria dei titoli derivati.

Teorema dei prezzi impliciti: per evitare arbitraggi deve sussistere l'uguaglianza: v(t;T;s)=v(t;s)/v(t;T) con t T s. Dimostrazione: se fosse v(t;s)>v(t;T)v(t;T;s) per effettuare arbitraggi potremmo adottare la seguente strategia: vendita allo scoperto del TCN unitario con scadenza in s; acquisto a pronti di v(t;T;s)unità del TCN unitario con scadenza in T; acquisto a termine, per consegna in T, del TCN unitario con scadenza in s.

Tassi impliciti: il tasso annuo d'interesse dell'operazione a termine regolata dal prezzo unitario v(t;T;s) è stato definito come: i(t;T;s)=[1/v(t;T;s)]^1/(s-T)-l. Se sono trattati sul mercato a pronti, i TCN con scadenza in T ed s, il tasso i(t;T;s) è implicito nei tassi a pronit i(t;T) e i(t;s). infatti, esprimendo i prezzi che compaiono nel teorema dei prezzi impliciti in funzione dei tassi annui secondo la relazione tipo: v(t;T;s)=[1+i(t;T;s)]^-(s-T) con t T s avremo: con t T s. 1+i(t;T;s)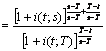. Esprimendo la prima espressione in termini di rendimenti a scadenza, usando: h(t;T;s)=log[1+i(t;T;s)] con t T s come relazione tipo, avremo: h(t;T;s)(s-T)=h(t;s)(s-t)-h(t;T)(T-t), da cui, ricavando h(t;s): h(t;s)=h(t;T)((T-t)/(s-t))+h(t;T;s)((s-T)/(s-t)). Il rendimento a scadenza sul periodo lungo [t;s] risulta perciò uguale alla media aritmetica ponderata dei due rendimenti a scadenza (uno a pronti, l'altro a termine) sui sottoperiodi contigui [t;T] e [T;s], essendo i pesi espressi dalla lunghezza relativa dei sottoperiodi.

Le strutture per scadenza a pronti: la disponibilità di m titoli con prezzi V(t;x_k) rende il mercato completo: sulla base di queste quotazioni vengono ricavati i prezzi v(t;t_k) degli m titoli elementari e qualsiasi altro titpo di titolo trattato in t è ridondante, nel senso che può sempre venire replicato da un portafoglio di titoli elementari e quindi valutato sulla base dell'espressione: V(t;z)=. La struttura per scadenza dei tassi d'interesse (a pronti) si ricava dai prezzi a pronti: . Naturalmente la struttura dei tassi ha lo stesso contenuto informativo della struttura dei prezzi; tuttavia il riferimento ai tassi di interesse risulta largamente preferito nella pratica del linguaggio finanziario.

Le strutture per scadenza implicite: se effettuiamo il calcolo del prezzo a termine, o implicito, relativamente ad ogni coppia di date contigue dello scadenzario s, otteniamo la struttura per scadenza dei prezzi impliciti al tempo t, che è quindi espressa dalle: v(t;t+k-l;t+k)=v(t;t+k)/v(t;t+k-l) con k=1,2,,m. La struttura dei tassi impliciti in vigore sul mercato al tempo t si ottiene calcolando, per k=1,2,m, i tassi d'interesse a termine uniperiodali: i(t;t+k-l;t+k)= Risulta insomma che la struttura dei tassi impliciti domina (o è dominata) la struttura dei tassi a pronti nei periodi in cui la struttura a pronti è crescente (decrescente). Analoga proprietà vale per le strutture, a pronti ed implicite, degli yeld to maturity. Dato che la struttura a pronti è monotona crescente, i tassi impliciti risultano tutti (escluso il primo) strettamente maggiori dei corrispondenti tassi a pronti.

Scadenzari discreti: supponendo che i titoli trattati sul mercato al tempo t possano garantire il amento di poste monetarie limitatamente alle date dello scadenzario t, la struttura per scadenza dei prezzi apronti definita da v(t;t_k)=V(t;x_k)/x_k con k=1,2,m, sarà ricavata una volta osservati i prezzi V(t;x_k) di m TCN che coprano tutte le scadenze. La struttura per scadenza dei tassi a pronti sarà espressa da: i(t;t_k)= e i(t;t_k-l;t_k)=. Tuttavia, in certi casi limite può essere utile fare riferimento a scadenzati discreti illimitati. L'estensione non comporta modifiche sostanziali delle considerazioni precedenti, salvo la richiesta che al tempo t siano osservabili i prezzi di TCN relativi ad un'infinità numerabile di scadenze e che questi prezzi decrescano, in funzione della scadenza, in modo da soddisfare particolari requisiti di convergenza.

Scadenza e vita a scadenza: in molti casi è significativo utilizzare una rappresentazione semplificata della struttura temporale del flusso x/t estraendo dall'insieme delle date dello scadenzario t un indice sintetico che ne riassuma le caratteristiche in modo sufficiente per certe specifiche applicazioni. L'indice sintetico più immediato, è, naturalmente, la scadenza t_m (maturity). Si definisce anche la vita a scadenza (time to maturity), o vita residua, come la differenza t_m-t. La maturity indica la data in cui il contratto si può considerare definitivamente concluso; la relativa vita a scadenza rappresenta la durata complessiva dell'operazione di scambio.

La scadenza media aritmetica: supposto un flusso x non contenente poste negative, restando inteso che almeno una delle poste è strettamente positiva, la scadenza media aritmetica è definita come 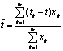e rappresenta quindi la media ponderata delle vite a scadenza t_k-t di tutte le poste, con i pesi: con k=1,2,,m espressi dai valori relativi dei singoli importi. La scarsa significatività di questo indice è legata all'eccessiva meccanicità della definizione.

La duration: sia v(t;s) la struttura dei prezzi a pronti in vigore sul mercato al tempo t. Sempre facendo riferimento ad un flusso di poste non negative, la duration al tempo t di x/t è definita come: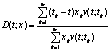 essendo con k=1,2,,m. Quindi d(t;x) è la media aritmetica ponderata delle vite a scadenza delle poste del flusso, essendo in questo caso, i pesi p_k calcolati in base alla struttura per scadenza in vigore sul mercato. L'uguaglianza della duration con la vita a scadenza di una delle poste di x/t può aversi solo nel caso degenere di "massa concentrata", cioè di un flusso di tipo TCN. D(t;s)=t_m-t è valida se e solo se l'unica posta non nulla del flusso x/t è l'importo x_m disponibile alla scadenza t_m.

La duration con struttura piatta: se la struttura dei tassi d'interesse è costante ad un livello i, cioè: i(t;s)= i costante con t s, si ha la duration a struttura piatta: 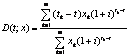. Nei casi in cui è possibile ricavare, unico, il tasso interno di rendimento i^* del flusso x/t sulla base del prezzo di mercato, la duration calcolata con struttura piatta al livello di i^* fornisce una soddisfacente approssimazione della duration.

Il caso di rendite a rate costanti: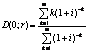 e risulta indipendente dal valore della rata R. Il denominatore dell'espressione è il valore attuale a_m]i=; il numeratore, invece (d_m]i) viene a volte indicato come la dollar duration della rendita unitaria r. Con alcuni semplici passaggi anche questa quantità può essere espressa in modo esplicito. Moltiplicando e dividendo per (1-v) si ottiene:. Sviluppando e dividendo per otteniamo: o anche, in termini di tasso: . Se ne deduce che la duration della rendita r è una funzione decrescente del tasso di valutazione ed è funzione crescente del numero di rate (cioè della maturity del flusso r). Risulta forse meno evidente il fatto che la duration non cresce illimitatamente al crescere della durata, dato che è si ricava che il grafico della D(0;r) in funzione di m presenta un asintoto orizzontale al livello (1+i)/i. Questo valore può essere interpretato come la duration di una rendita perpetua posticipata.

Il caso di titoli a cedola fissa: evidentemente, il titolo a cedola fissa x è equivalente ad un portafoglio composto da una rendita I posticipata con m rate annue I e da un TCN unitario con maturity m e valore facciale C. Si avrà cioè: V(0;x)=V(0;I)+Cv(0;m). Quindi, la duration del titolo a cedola fissa può essere calcolata come media pesata della duration D(0;I) del flusso cedolare I calcolata secondo la duration per rendite a rate costanti in funzione del tasso, e della duration m del TCN che corrisponde al rimborso del valore nominale C. Naturalmente, se è I=0, il titolo si riduce ad un TCN con valore facciale C e si ha D(0;x)=m. In tutti i casi in cui il titolo è effettivamente dotato di flusso cedolare, cioè se I>0, la duration risulta funzione decrescente sia del tasso i di valutazione, che del tasso cedolare I/C. Inoltre, al variare della maturity m la duration ammette ancora il calore asintotico (1+i)/i, come per le rendite a rata costante. Precisamente, se si aumenta la vita a scadenza del titolo,, la duration risulta avere andamento strettamente crescente quando il tasso di valutazione non supera il tasso cedolare, cioè se I/C i; invece per valori più bassi della cedola, cioè per I/C<i, la duration del titolo arriva a superare il livello asintotico, crescendo fino ad un valore massimo, raggiunto il quale comincia a decrescere, avvicinandosi dall'alto al valore (1+i)/i.

Momenti di second'ordine: se si misurano i tempi a partire dall'istante t, la duration rappresenta l'ascissa del baricentro, fornisce cioè il momento del primo ordine della distribuzione p_k. Il momento di second'ordine, o duration di second'ordine è definito da: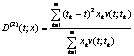. La duration di second'ordine esprime la media pesata dei quadrati degli scarti temporali (t_k-t) e fornisce quindi una misura di dispersione temporale del flusso x rispetto a t. Non può assumere valori negativi:0 (t₁-t)² D⁽²⁾(t;x) (t_m-t)² e coincide con il quadrato della vita a scadenza di una delle poste di x/t solo nel caso di massa concentrata. Evidentemente, la duration di secondo ordine, ha dimensioni di tempi al quadrato, dato che esprime una media di tempi²: si definisce quindi l'indice temporale noto come dispersione temporale del flusso x/t, che ha per dimensioni un tempo.

Duration e dispersione di portafogli: consideriamo, al tempo t, n flussi non nulli x_i definiti, senza perdita di generalità sullo scadenzario comune t_i. A partire da questi flussi è sempre possibile costruire un portafoglio: a a a a_n contenente a_i unità del titolo x_i. Da questo punto di vista è significativo considerare l'insieme dei flussi x_i come un paniere, dal quale viene selezionato il portafoglio a. Il flusso z dei amenti generati dal portafoglio, si ottiene sommando, per la generica scadenza k, tutte le poste esigibili in t_k dei titoli del paniere, prese secondo la relativa quota di composizione. Si ha cioè: z/t= / essendo z_k= con k=1,2,,m. V(t;z)=. Il valore attuale del portafoglio può quindi essere calcolato a partire dal valore dei flussi componenti, effettuandone la combinazione lineare con coefficienti uguali alle quote di composizione.

L'evoluzione della struttura per scadenza dei tassi d'interesse: a partire da v(t;s) è possibile ricavare la struttura dei tassi e delle intensità d'interesse, a pronti ed a termine, e si può effettuare la valutazione di arbitraggio di tutti i titoli trattati. Ogni modello evolutivo per il mercato dinanziario, e quindi per la struttura per scadenza dei tassi d'interesse, dovrà tenere conto correttamente del ruolo dell'incertezza, basandosi su opportune ipotesi probabilistiche sullo stato futuro del sistema economico.

Teorema dei prezzi certi: in condizioni di certezza, per evitare arbitraggi non rischiosi, deve sussistere l'uguaglianza: . Dimostrazione per assurdo: se fosse V(t;x)>v(t;t')V(t';x), si potrebbe adottare la seguente strategia di compravendita: vendita allo scoperto in t del titolo che garantisce il flusso x/t; acquisto a pronti in t di V(t';x) unità del TCN unitario scadente in t'; acquisto a termine in t, per consegna in t' del titolo che fornisce il flusso x/t. La tabella dei pay-off dimostra che questa strategia porterebbe ad un arbitraggio ti tipo B. Il teorema dei prezzi certi afferma che in condizioni deterministiche, il prezzo futuro del titolo viene necessariamente determinato moltiplicando il prezzo corrente per il fattore di capitalizzazione m(t;t')= 1/v(t;t') in vigore sul mercato in t per l'orizzonte di investimento [t;t']. Se il titolo considerato è un TCN unitario, l'uguaglianza assumerà la forma: con t t' s ovvero v(t';s)=v(t;t';s) con t t' s. Nel caso del generico flusso x, per la proprietà di linearità si ottiene: V(t';x)=V(t;t';x). Risulta quindi che, in condizioni di certezza, i prezzi a pronti futuri debbono coincidere aon gli attuali prezzi a termine. Com'è noto, la scindibilità implica l'indipendenza da t della funzione intensità istantanea d'interesse: d(t';s)=d(t;s) con t t' s per cui è come se il mercato fosse regolato da un unico contratto, fissato una volta per tutte in un arbitrario istante di tempo.

Le ipotesi di aspettativa: in condizioni di perfetta prevedibilità le ipotesi di mercato richiedono che i tassi a pronti futuri coincidano con i tassi forward correnti: i(t';s)=t(t;t';s) con t t' s. In condizioni di incertezza, i tassi futuri i(t';s) sono numeri aleatori nell'istante t, perché in generale sono aleatori in t i prezzi futuri V(t';x) di qualsiasi flusso x di amenti. Le differenti teorie per la struttura per scadenza dei tassi d'interesse proposte nella letteratura tradizionale, possono essere enunciate proprio formulando ipotesi sulle aspettative. Indicando con E_t(X) l'aspettativa al tempo t della variabile aleatoria X² si può distinguere tra diversi tipi di ipotesi:

ipotesi della pura aspettativa: (aspettativa non distorta) si tratta della schematizzazione più semplice, secondo la quale il valore fissato dal mercato per i tassi a termine coincide esattamente con il valore che il mercato si aspetta per i tassi a pronti futuri: i(t;t';s)=E_t[i(t';s)] con t t' s. In altri termini, i tassi forward costituiscono un'aspettativa non distorta dei futuri tassi a pronti.

Ipotesi della preferenza per la liquidità: empiricamente, i prezzi di titoli di lunga durata risultano maggiormente sensibili a variazioni della struttura dei tassi rispetto ai titoli di durata più breve. Per questo motivo, gli agenti economici considerano i titoli a lungo termine come investimenti più rischiosi, es essendo avversi al rischio, preferiscono l'acquisto di titoli più "liquidi" cioè con più breve maturity: i(t;t';s)= E_t[i(t';s)]+p(t;t';s) con t t' s dove p(t;t';s) 0 rappresenta il tasso di rendimento aggiuntivo corrispondente al premio di liquidità. Si suppone che questo rischio aumenti sia aumentando il differimento dell'investimento che allungandone la durata. Quindi, il premio per la scadenza p(t;t';t'+t) dovrà essere una funzione non decrescente di t' e di t

Ipotesi dei mercati segmentati: i prezzi di titoli con vita a scadenza molto diversa non possono essere rigidamente interconnessi tra loro sulla base del principio di esclusione degli arbitraggi, poichè investitori diversi preferiscono detenere titoli appartenenti ad un particolare segmento dell'asse delle maturity, senza tenere conto dei prezzi degli altri titoli.

Ipotesi dell'habitat preferito: si suppone che il mercato dia popolato da agenti che, pur avendo una convenienza ad investire su un determinato segmento di maturity, sono disposti ad uscire da questo "habitat preferito" investendo anche su titoli con vita a scadenza diversa se questi offrono un adeguato premio in termini di extrarendimento. Si può assumere che i prezzi di titoli di diversa scadenza siano collegati tra loro tramite precise dipendenze funzionali e si può ancora ipotizzare una relazione tra tassi ed aspettative formalmente identica a quella dell'ipotesi di preferenza della liuidità. In questo caso, tuttavia, non sono richieste limitazioni né sul segno né sulla monotonia dei premi per la scadenza p(t;t';t+t

Operazioni finanziarie rischiose: la teoria delle decisioni finanziarie in condizioni di incertezza, ha per oggetto lo studio delle operazioni di scambio di importi monetari aleatori, la cui entità, cioè, non è nota con certezza nel momento i cui lo scambio viene pattuito. Con riferimento alle conseguenze, favorevoli o sfavorevoli, che possono derivare dalla stipula di un contratto simile, si usa parlare di operazioni che comportano un rischio finanziario. Il guadagno dell'individuo I nell'operazione, sarà espresso da G=X₂-X₁; si tratta ovviamente, di un guadagno algebrico, dato che, in generale, la variabile aleatoria G potrà assumere determinazioni negative.

L'insieme delle distribuzioni: le variabili aleatorie X appartenenti all'insieme delle alternative sono completamente descritte dalla distribuzione di probabilità ad essa attribuita dall'individuo I. Il problema decisionale può allora essere inteso come un problema di ordinamento tra tutte le distribuzioni di probabilità disponibili al momento della scelta. Indicando con F_k(x)=P(X_k x) la funzione di ripartizione della variabile aleatoria X_k, e se si indica con F l'insieme delle funzioni di ripartizione delle variabili aleatorie X appartenenti all'insieme di opportunità, affinché l'individuo possa effettuare scelte razionali tra gli elementi, egli dovrà avere costituito una relazione di preferenza, tale che, comunque scelte due distribuzioni F₁ ed F₂ appartenenti all'insieme, di possa decidere se una di esse è preferita all'altra, o se le due distribuzioni siano indifferenti.

Dominanza stocastica: si possono introdurre ordinamenti parziali nell'insieme F seguendo dei criteri basati su ipotesi generali. Supponiamo F₂(x) F₁(x) con x appartenente all'insieme dei numeri reali, e che la diseguaglianza valga in senso stretto per almeno un valore di x. Questa proprietà, detta di dominanza stocastica del primo ordine, stabilisce che, comunque fissato il numero reale x, la probabilità che la situazione patrimoniale X₁ risulti maggiore di x non è mai maggiore della probabilità che X₂ risulti maggiore di x. Sotto opportune ipotesi di continuità, si può dimostrare che se F₂ domina F₁ nel senso della precedente disuguaglianza, allora, ogni individuo che sia massimizzatore di profitto, preferirà X₂ ad X₁. La dominanza stocastica va quindi vista come un requisito necessario, ma largamente insufficiente per la costruzione di un criterio generale di scelta.

Posizioni finanziarie composte: si tratta di situazioni finanziarie incerte in cui possono venire a trovarso gli individui chiamati a scegliere tra due situazioni finanziarie X₁ e X₂, anch'esse incerte, a seconda dell'esito che avrà un certo evento A, al cui verificarsi, l'individuo attribuisce una probabilità P(A)=a di valore strettamente compreso tra 0 ed 1. Nel linguaggio del calcolo delle probabilità, la posizione composta è rappresentata da una variabile aleatoria mistura, indicata con X₁aX₂, che ha come possibili determinazioni, sia le determinazioni di X₁ che quelle di X₂, e che assumerà le prime con probabilità a, e le seconde con probabilità (1-a). Si può allora richiedere, come caratteristica di razionalità, che, se l'individuo preferisce X₂ ad X₁, allora, qualsiasi mistura di X₁ e X₂ sarà preferita ad X₁, mentre X₂ sia preferita a qualsiasi mistura di X₁ e X₂.

Assioma di consistenza: per ogni X₁ ed X₂ appartenenti ad X, tali che X₂ sia preferito ad X₁, e per ogni numero reale a maggiore di 0 e minore di 1, dovrà aversi: . In base alla proprietà delle probabilità condizionate, è immediato mostrare che la funzione di ripartizione F₃(x)=P(X₁aX₂ x) della mistura X₁aX₂ è data dalla combinazione lineare, con coefficienti a e (1-a) delle funzioni di ripartizione F₁(x) e F₂(x) di X₁ ed X₂. Quindi:.

Teorema di rappresentazione: se l'ordinamento di preferenza definito su X p completo, consistente e coerente con la relazione di dominanza stocastica, allora:

Esiste una funzione v(x) tale che se e solo se: E[v(X₂)]>E[v(X₁)]

La funzione v(x) è l'unica a meno di una trasformazione lineare positiva crescente. Quindi, qualsiasi funzione z(x) che sia ottenuta effettuando una trasformazione lineare positiva di v(x), cioè tale che z(x)=av(x)+b con a costante positiva e b costante arbitraria, induce in X lo stesso ordinamento.

Criterio della speranza matematica: la speranza matematica del guadagno E(G) deriva dall'aver assegnato alla funzione v(x), considerata nel teorema di rappresentazione, la forma di una qualsiasi funzione lineare crescente, accettando quindi, implicitamente, di caratterizzare solamente il comportamento di un individuo che sia massimizzatore di profitto: E(X₂)-E(X₁)>0 e cioè: E(G)>0. L'operazione di scambio di X₂ con X₁ verrà quindi valutata in base al segno di E(G): secondo tale criterio, l'operazione sarà definita: favorevole se E(G)>0, equa se E(G)=0, sfavorevole se E(G)<0. In questo contesto, il criterio seguito nella teoria delle decisioni in condizioni d'incertezza sarà quello della massimizzazione del guadagno sperato.

Principio dell'utilità attesa: seguendo la linea presentata da Bernoulli, per la risoluzione le paradosso di Pietroburgo, per ovviare a queste difficoltà è sufficiente cambiare la scala con cui si misurano gli importi, sostituendo la scala del valore monetario con una scala soggettiva basata sull'utilità; viene cioè introdotta una funzione u(x) del capitale x, detta funzione di utilità, la quale rappresenta l'importanza che ha per un dato individuo il possesso del capitale x. Sulla base del teorema di rappresentazione, l'opportunità X₂ sarà preferita ad X₁ se e solo se E[u(X₂)]>E[u(X₁)]. Il criterio decisionale derivante da questa impostazione consisterà nella massimizzazione dell'utilità sperata. In base a questo criterio, diremo che, se un individuo dotato di funzione di utilità u(x) si trova nella situazione finanziaria X₁, egli reputerà l'operazione consistente nello scambiare X₂ con X₁: vantaggiosa se E[u(X₂)]-E[u(X₁)]>0, indifferente se E[u(X₂)]-E[u(X₁)]=0, svantaggiosa de E[u(X₂)]-E[u(X₁)]<0. E' appena il caso di notare, che se la funzione id utilità è lineare, cioè se u(x)=ax+b, con a reale positivo, allora si avrà sempre: E[u(c+G)]-u(c)=E[a(c+G)+b]-(ac+b)=aE(G) e quindi ci si riconduce al criterio della speranza matematica; perciò un individuo che abbia funzione di utilità lineare ritiene indifferente un'operazione equa.

La scala dell'utilità: l'ipotesi fondamentale su u(x), oltre a quella naturale di crescenza, è che ad incrementi uguali di capitale, corrispondono incrementi di utilità tanto più piccoli quanto più grande è il capitale posseduto dall'individuo: u(x')>u(x) se x'>x e u(x+x₀)-u(x)>u(x'+x₀)-u(x') se x'>x ed x₀>0. Converrà inoltre supporre che u(x) sia funzione continua su tutto il suo insieme di definizione. Se scegliamo due incrementi x₀ consecutivi a partire da (x-x₀) potremo scrivere: u(x)-u(x-x₀)>u(x+x₀)-u(x) cioè: .

Proprietà differenziali della funzione di utilità: se si suppone u(x) dotata di derivata prima u'(x), le proprietà della scala dell'utilità richiedono che questa sia una funzione positiva decrescente di x. Se si definisce u'(x) come l'utilità marginale del capitale x, allora l'ipotesi di monotonia su u(x) richiede che l'utilità marginale sia non negativa, e la proprietà di concavità si esprime usialmente dicendo che l'utilità marginale diminuisce all'aumentare del capitale. Individui contraddistinti da una funzione di utilità con derivata seconda negativa so dicono avversi al rishio. Nei casi di derivata seconda maggiore o uguale a 0, si parlerà di individui propensi o indifferenti al rischio.

Una misura dell'avversione al rischio: viene chiamata misura assoluta di avversione al rischio. Si tratta di una quantità direttamente collegata alla concavità relativa della funzione di utilità, ed è locale, in quanto misura la concavità di u(x) solo in un intorno di x. Se si calcola invece la misura di avversione al rischio di Arrow-Pratt, si ottiene: . Il coefficiente di avversione al rischio r(x) avrà le dimensioni del reciproco di un importo e si misurerà quindi in lire^-l. A sua volta, il reciproco di r(x): B(x)=1/r(x) avrà dimensioni in lire, e rappresenterà un importo tanto più grande quanto meno l'individuo è avverso al rischio. B(x) fornirà quindi la misura della tolleranza al rischio dell'individuo. In molte applicazioni della teoria dell'utilità è importante supporre che r(x) dia una funzione non crescente di x. L'ipotesi di avversione al rischio decrescente non è necessaria per sviluppare la teoria dell'utilità attesa e vengono spesso prese in considerazione le funzioni u(x) che non soddisfano questa proprietà.

Utilità logaritmica: assume l'incremento di utilità come direttamente proporzionale (a meno di infinitesimi di ordine superiore) all'incremento di capitale ed inversamente proporzionale al capitale posseduto: du=a dx/x con a>0 da cui u(x)= a log x +b con x>0 dove a e b sono costanti arbitrarie (a>0). L'avversione al rischio è data da r(x)= 1/x e soddisfa perciò l'ipotesi di decrescenza.

Utilità esponenziale: in alcune applicazioni è conveniente riferirsi a funzioni di utilità superiormente limitate. con a>0 che ha come estremo superiore il parametro a (potenzialità massima). La proprietà caratteristica di questa funzione consiste nell'avere l'avversione al rischio costante; infatti si ricava immediatament che è r(x)= 1/a. È facile mostrare che, se si esclude il caso delle funzioni lineari, per le quali risulterebbe r(x)=0, le funzioni dell'utilità esponenziale sono lo uniche dotate di questa proprietà. Inoltre, sotto l'ipotesi di utilità esponenziale, un'operazione somma di più operazioni indipendenti ed indifferenti è a sua volta indifferente.

Utilità quadratica: in molte applicazioni viene ipotizzata una funzione di utilità di tipo quadratico, espressa nella forma: con a>0. La concavità è assicurata dalla non negatività del parametro a. L'utilità marginale è u'(x)=l-ax ed il coefficiente di avversione al rischio è dato da: r(x)=a/(l-ax). L'avversione al rischio ha quindi un andamento iperbolico e, nel dominio di definizione D=(0;1/a) è una funzione crescente di x come risulta anche dal segno positivo della derivata di r(x) che ha espressione

Funzioni di utilità di tipo HARA: una classe di funzioni di utilità d'importanza rilevante in economia finanziaria è quella costituita dalle funzioni dotate di avversione al rischio r(x) iperbolica, dette appunto di tipo HARA. In questa classe, r(x) ha la forma: con a₁ e a₂ costanti tali da garantire valori sempre positivi di r.

L'equivalente certo: il valore atteso di X sarà dato da e l'utilità attesa sarà: . Per l'ipotesi di concavità sulla u(x), avremo E[u(X)] u[E(X)] o anche: avendo indicato con U(X) l'utilità sperata dell'importo X. La prima diseguaglianza, è conosciuta anche come disuguaglianza di Jensen. Nei termini della teoria dell'utilità, la * afferma che l'utilità sperata di un importo aleatorio non è mai superiore all'utilità dell'importo sperato. Per l'ipotesi di monotonia, il segno di uguaglianza vale solo se X è una variabile aleatoria degenere. Si definisce equivalente certo dell'importo aleatorio X (in base alla funzione di utilità u(x)) l'importo certo m_u che produce un'utilità uguale all'utilità sperata dell'importo aleatorio X; m_u si può anche intendere come il prezzo che si è disposti a are per acquisire il diritto di partecipare ad una scommessa che ponga nella situazione incerta X. m_u=x: u(x)=E[u(x)] cioè: m_u=u^-l dato che u(x), per l'ipotesi di monotonia e continuità, è dotata di funzione inversa u-l. Quindi, calcolando la funzione u^-l per ambo i membri della prima diseguaglianza, il verso della diseguaglianza si conserva: u^-l u^-l o anche m_u m, avendo indicato con m la speranza matematica di X. Si ricava quindi che l'equivalente certo di un importo aleatorio X non è mai superiore alla speranza matematica di X. il segno di uguaglianza cale solo nel caso di X degenere. E' interessante notare che l'equivalente certo m_u è una medi associativa, essendo una trasformata monotona della media aritmetica m=E(X); ed anzi m_u m può essere vista come una particolare diseguaglianza tra medie associative. Se la u(x) è dotata di derivata seconda, si può dimostrare che l'equivalente certo di X per un individuo è tanto minore quanto maggiore è la sua avversione al rischio. E[u(c+G)] u[E(c+G)] se l'operazione è equa, si avrà E(G)=0, cioè E(c+G)=c, e perciò E[u(c+G)]-u(c) 0; l'operazione è quindi svantaggiosa. Questo significa che un individuo avverso al rischio considera svantaggiosa un'operazione finanziaria (aleatoria) equa, cioè non accetta di scambiare un capitale certo c con un capitale aleatorio X₂=c+G di valore sperato E(X₂)=c.