CARICA E SCARICA DI UN CONDENSATORE

PREMESSA

Un conduttore isolato nello spazio e lontano da altri corpi elettrizzati, avente carica Q, è soggetto all'azione del campo elettrico da esso creato e quindi ha un potenziale V0.

Aumentando Q aumenta anche V : si verifica che esiste una diretta proporzionalità tra V e Q , ovvero che Q/V = C cost

La costante C è detta capacità elettrostatica del conduttore e si misura in Farad [C/V], 1F = 1 C/ 1V.

Se vicino al conduttore si pone un altro conduttore scarico, per effetto dell'induzione elettrostatica sul conduttore scarico si creano cariche indotte che alterano il potenziale del primo conduttore; esso diviene minore e quindi la capacità aumenta. Un metodo per aumentare la capacità C di un conduttore è quindi quello di porlo vicino ad un altro conduttore scarico.

Un condensatore è un dispositivo costituito da due conduttori affacciati, detti armature, disposti in modo tale da avere una elevata capacità. Il condensatore piano in particolare, è costituito due lamine metalliche piane di area S, poste, parallele, a distanza d l'una dall'altra ( con S>>d); tra esse può esservi il vuoto oppure un dielettrico.

Caricando una armatura a +Q e ponendo l'altra armatura a terra, su quest'ultima viene indotta una carica -Q. Il campo elettrico che si crea tra le armature del condensatore piano è uniforme.

Indicando con V₂ e V₁ i potenziali elettrici assunti dalle due armature

quando posseggono cariche +Q e -Q, si ha che la ddp tra le armature

è proporzionale a Q : Q = C (V₂ - V₁)

In tal modo la capacità del condensatore è C = Q/DV

Dalle relazioni esistenti tra Q, V ed E si ottiene:   

Si ha cioè che la capacità del condensatore piano è direttamente proporzionale a e_r e a S, ed inversamente proporzionale a d .

Per caricare un condensatore occorre compiere un lavoro ( il trasferimento della carica +Q da un'armatura all'altra provoca una resistenza da parte delle cariche stesse):

che rappresenta il lavoro fatto dalla carica Q per passare dal potenziale V₂ al potenziale V_1.

PROCESSO SI SCARICA

Consideriamo un circuito in condizioni quasi stazionarie, ovvero lentamente variabili nel tempo. Istante per istante si può pensare il circuito in equilibrio, naturalmente con valori istantanei delle grandezze in gioco.

Possiamo allora applicare a tali circuiti la legge di Ohm generalizzata e le regole di Kirkhoff come relazioni tra valori istantanei delle grandezze.

Nel caso della scarica (carica) di un condensatore piano C attraverso una resistenza R si ha un circuito in condizioni quasi stazionarie.

Supponendo che C abbia carica Q₀ e ddp V₀, si chiuda l'interruttore all'istante t=0.

Le cariche elettriche (corrente i) fluiranno e attraverso R verrà dissipata energia.

La carica su ogni armatura, la ddp ai capi di C e l'energia immagazzinata decresceranno nel tempo.

Il condensatore, rispetto a R, funge da generatore di f.e.m.

variabile e resistenza interna uguale a zero.

L'equazione del circuito istante per istante, sarà:

V(t) = R i(t)

Sostituendo: e si ottiene:

Ovvero

(OSS) il segno meno indica che dQ è la variazione di carica sulle armature e non la carica che passa nel conduttore dq=-dQ)

Integrando l'ultima equazione di ottiene:

    ovvero

poiché Q(t=0) = Q₀ = V₀ C k = Q₀

quindi in definitiva: 

Si ha cioè che la carica Q ( e la ddp Q/C) decade esponenzialmente. La costante (tau) t = RC ha le dimensioni di un tempo e caratterizza la rapidità della scarica :

per t = t si ha Q = Q₀/e che indica la riduzione della carica dopo t sec.

t  si dice costante di tempo del circuito .

La corrente i di conduzione è:

ovvero sapendo che Q₀ = V₀ C

e decade esponenzialmente con la stessa costante di tempo t di Q.

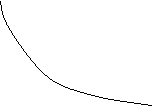i

f/RC

(R+r)C t

PROCESSO DI CARICA

Anche nel caso della carica di un condensatore di capacità C da parte di f.e.m. (f,r) attraverso una resistenza R, si applicano le leggi dei circuiti istante per istante; man mano che si carica C si comporta come un generatore di f.e.m. (f = V(t), r = 0) diretta in verso opposto alla f del generatore, poiché le cariche accumulate sulle armature tendono a spingere le cariche in verso opposto a quello della corrente prodotta da f.

Applicando al circuito la legge delle maglie, si avrà:

e, anche in tal caso (essendo e )

si ottiene:   

la soluzione di questa equazione differenziale, ponendo le condizioni iniziali è:

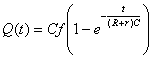
da cui

con

Q ed i crescono esponenzialmente con la costante di tempo t. Il valore finale di Q sarà Cf ed il corrispondente valore di V sarà f.

Q

Cf

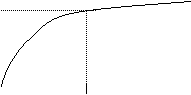
(R+r)C t

L'ESPERIMENTO

SCOPO:

verificare la carica e la scarica di un condensatore di capacità C attraverso una resistenza R collegata in serie, secondo la legge esponenziale (dal grafico). Verificare inoltre che la costante di tempo del circuito t = RC rappresenta il tempo necessario affinché la ddp tra le armature sia circa il 63% del valore della tensione applicata mediante il generatore.

MATERIALE:

generatore di tensione continua

condensatore elettrolitico di capacità C mF

resistenza R 1 MW

voltmetro

conduttori di collegamento

due interruttori

contasecondi

OSS:

R deve essere >> di C perché altrimenti il tempo di scarica (carica) è troppo breve

Si potrebbe realizzare un circuito con 2 resistenze una per la carica e l'altra per la scarica di C, ma poiché è impossibile trovarle esattamente uguali, si utilizza una sola resistenza e due interruttori che permettono di escludere una parte di circuito: essi non andranno mai chiusi contemporaneamente altrimenti si cortocircuita.

Se il condensatore è stato a lungo inattiva si deve caricarlo e poi scaricarlo prima dell'esperimento collegando tra loro i due poli mediante un conduttore (messa a terra)

ESECUZIONE

Si procede montando il circuito  

R

+ I₂ + C V

- -

I₁

Oss: il condensatore elettrolitico è polarizzato, quindi bisogna stare attenti al verso della corrente.

PROCESSO DI CARICA

Chiudendo I₁ , C si carica : controllo sul voltmetro che l'indice devia fino ad un valore pari alla f.e.m. fornita ( V = 20Volt) .

Apriamo I₁ e chiudiamo I₂ : C si scaricherà attraverso R fino ad avere V = 0.

Oss: eliminando R la carica sarebbe istantanea.

Disponendo di un interruttore a tasto si può montare il circuito come segue, escludendo il voltmetro ed inserendolo solo per le letture.  R I₂

Chiudendo I₂ solo per il tempo necessario alle misure,

si hanno risultati più attendibili: l'inserimento di V

altera il valore della resistenza + C

- V

I₁

Per ottenere una analisi quantitativa della carica, inseriamo un cronometro alla chiusura di I₁ e rileviamo i valori di V ad intervalli regolari ( 5 secondi)

OSS: se i tempi sono troppo brevi occorre aumentare il valore di R.

Raccogliamo quindi i dati in una tabella .

Costruiamo quindi, su carta millimetrata un grafico: i rettangoli che indicano l'incertezza assoluta delle misure, sono tutti uguali; il valore limite di V e quello della tensione di alimentazione V₀.

L'andamento esponenziale conferma la legge teorica (trascurando la resistenza interna del generatore, r): 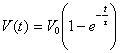con t = RC

Individuando sul grafico il punto di ascissa t, ovvero (RC,0), si determina il corrispondente punto della curva che, nei limiti dell'errore, avrà ordinata pari a circa il 63% di V₀.

Ciò conferma il significato fisico della costante di tempo t

V

V₀

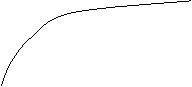
63% V₀

t=RC t

ERRORI

L'errore su assoluto su V è:   

(Cl_p: classe di precisione dello strumento;

V_fs valore di fondoscala usato nella corrispondente misura di V)

Dt corrisponde alla minima divisione della scala del cronometro.

PROCESSO DI SCARICA

Si può verificare il significato di t anche nel processo di scarica: caricando C per un tempo pari almeno a 3t, si apre l'interruttore I₁ e si rilevano le tensioni ad intervalli regolari di tempo.

Si raccolgono i dati in una tabella uguale alla precedente, nella quale si evidenzia l'andamento decrescente di V

L'elaborazione della misura porta ad un grafico nel quale il corrispondente valore di V per t=t è pari a circa il 37% del valore iniziale della tensione (cioè C ha scaricato circa il 67% del valore iniziale).

V

V₀

37% V₀

t=RC   t

Analoghe esperienze si possono fare misurando i(t), cioè inserendo (in serie) l'amperometro al posto del voltmetro:

R

I₂

I₁ C

A G

Aprendo I₁ e chiudendo I_2, C si scarica; l'amperometro registra l'intensità della corrente durante la scarica, osservata a intervalli regolari di tempo (ad esempio 5 secondi) finchèin tale uintervallo il valore di i diventa molto basso e senza apprezzabili variazioni.

Si ripete più volte con calori diversi di R e di C

Ad esmpio:

- R = 200 KW C = 100 mF

- R = 200 KW C = 200 mF

- R = 400 KW C = 100 mF

Si riportano i dati in 3 tabelle del tipo:

E si riportano i dati su un grafico t-i; anche in tal caso si osserva un andamento esponenziale.

Il tempo di dimezzamento t_1/2 dipende dai valori di R e C; il rapporto t_1/2/RC