GLI ERRORI DI MISURA

GLI ERRORI DI MISURA

Prerequisiti: conoscenza del piano sectiunesiano e delle funzioni lineari, della media matematica, degli istogrammi, dell'ordine di grandezza di un numero e del concetto di grandezza derivata.

In fisica le grandezze fisiche e le unità di misura ci permettono di misurare i fenomeni che avvengono nel mondo che circonda e ci permettono di conoscere le proprietà degli oggetti che sono presenti in esso, come per esempio la quantità di materia che li costituisce, la loro lunghezza o la loro temperatura.

Queste grandezze non sono indipendenti tra di loro, ma sono correlate tramite delle leggi fisiche, come per esempio la relazione tra gradi Fahrenheit e i gradi Celsius che servono per misurare la temperatura di un corpo è espressa dalla legge t_f = 9/5^.t_c+32.

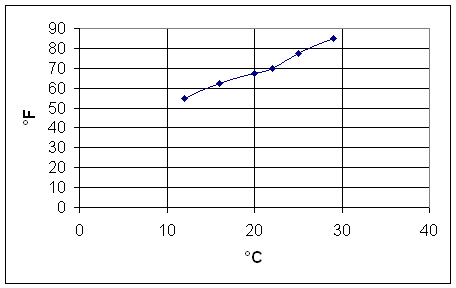Durante la misura delle grandezze fisiche è sempre presente un errore di misurazione che ci porta ad approssimare il valore della misura stessa, tornando alla legge t_f = 9/5^.t_c+32, il termometro quindi visualizza dei valori non precisi dei °F e quindi, nonostante la legge sia una funzione lineare, rappresentando i valori di t_f (visualizzati dal termometro con scala in gradi Fahrenheit) e t_c (visualizzati dal termometro con scala in gradi Celsius) sul piano sectiunesiano non otterremo una linea retta.

Gli errori di misura sono quasi sempre dovuti a delle imprecisioni degli strumenti di misura ed è quindi molto importante sceglierli in alla loro portata, sensibilità, precisione e prontezza. La portata di uno strumento indica la massima quantità che si può misurare con esso; la sensibilità è la più piccola variazione della grandezza che può essere misurata con lo strumento; la precisione indica la qualità dello strumento; la prontezza indica la rapidità con cui lo strumento risponde a variazioni della grandezza da misurare.

Gli errori si dividono in due tipi, sistematici e accidentali: quelli sistematici sono dovuti per lo più alla cattiva qualità degli strumenti di misura e sono errori che si presentano in tutte le ripetizioni di una data misurazione arrotondando il reale valore della misura per eccesso o per difetto; gli errori accidentali sono errori sperimentali imprevedibili che influiscono sul risultato della misura, spesso dovuti all'imperfezione degli strumenti o ad errori di misura da parte dello sperimentatore.

Questi due tipi di errori non si possono mai eliminare del tutto, ma si può avere un idea del loro valore ripetendo più volte la misurazione e calcolando il valore medio dei valori ottenuti. Il valore medio v_m di un numero n di misure si calcola facendo la somma di tutte le misure diviso il loro numero n :  

v_m = (x₁+x₂+ . +x_n)/n

Se per esempi misurando la lunghezza di un oggetto ottenendo i valori riportati in tabella, applicando la formula abbiamo che il valore medio è uguale a 0.69 m

v_m = (x₁+x₂+x₃)/3 = (0.5m+0.7m+0.87m)/3 = 0.69m

Un altro tipo di errore è l'errore assoluto o massimo che si ottiene facendo la semidifferenza tra il valore massimo delle misure e quello minimo:

e_m = (x_max-x_min)/2

Nell'esempio precedente l'errore massimo è:

e_m = (x_max-x_min)/2 = (0.87m-0.5m)/2 = 0.185m

Dividendo il valore massimo per il valore medio delle misure si ottiene l'errore relativo e_r che da informazione su quanto l'errore massimo incide sulla misura:

e_r = e_m/v_m

Nell'esempio:

e_r = e_m/v_m = 0.185m/0.69m =0.268

Esprimendo l'errore relativo in forma percentuale (cioè sotto forma di frazione di 100) si ottiene l'errore relativo percentuale e_%

e_% = e_r^.100

Nell'esempio:

e_% = e_r^.100 = 0.268^.100 = 26.8%

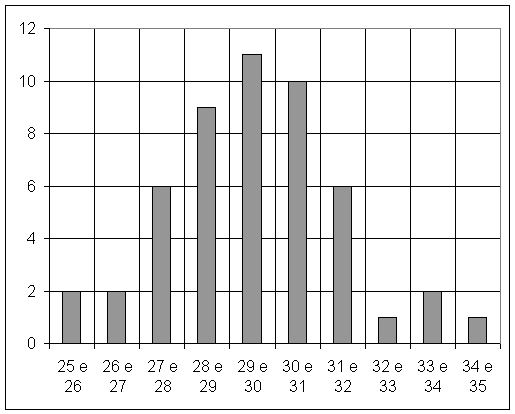
Un altro errore è quello statistico che si ha quando si effettua una misura molto complessa e quindi dove otteniamo molti valori di misura che possiamo rappresentare attraverso un istogramma (metodo di rappresentazione formato da colonne parallele di diversa altezza ognuna delle quali corrisponde ad un determinato valore). Grazie a questa rappresentazione dei valori, e quindi dell'errore statistico, si può notare che unendo le cime delle colonne si ottiene una curva che presenta la stessa forma anche se si rappresentassero i valori di altre misurazioni complesse. Questa curva prende il nome di "curva di Gauss".

Se una grandezza è derivata, gli errori di cui essa è affetta dipendono dagli errori contenuti nelle misure delle grandezze da cui essa deriva: per esempio l'errore massimo di una grandezza derivata dal prodotto di due misure è uguale al prodotto degli errori massimi delle misure da cui essa deriva.

Le misure delle grandezze fisiche sono espresse tramite delle cifre e queste sono chiamate cifre significative che si dividono in certe e in incerte. Quella incerta è l'ultima cifra scritta a destra ed essa deve essere dello stesso ordine di grandezza dell'errore di misura; quelle certe sono le cifre scritte a sinistra di quella incerta. Per esempio del numero 12345.67 ± 0.01 le cifre certe sono 1, 2, 3, 4, 5, 6 e la cifra incerta è il 7 che è dello stesso ordine di grandezza dell'errore 0.01.

Per quanto riguarda il numero di cifre significative di una grandezza derivata, questo è uguale a quello della misura della grandezza meno precisa (e quindi con il minore numero di cifre significative) da cui deriva.