 |  |
| |
 |
fisica |
|
I MOTI PIANI
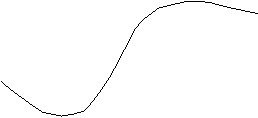
I moti piani sono tutti i moti che avvengono in un piano, il più comune dei quali è il moto dei proiettili.
La traiettoria non è rettilinea ma può essere definita come quella dei moti rettilinei:
TRAIETTORIA = insieme dei punti dello spazio che il corpo occupa al trascorrere del tempo
Per poter descrive il moto occorre inserirlo in un sistema di
riferimento e individuare la posizione del punto in ogni istante.
R
x (ascissa)
O
Un punto P può essere individuato mediante le coordinate sectiunesiane: P(x;y) oppure mediante le coordinate polari con distanza R e angolo α: P(R; α).
COME PASSARE DALLE COORDINATE POLARI A QUELLE CARTESIANE
COME PASSARE DALLE COORDINATE CARTESIANE A QUELLE POLARI
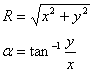
II
I
ESTENSIONE DELLA DEFINIZIONE DI SENO E COSENO
y
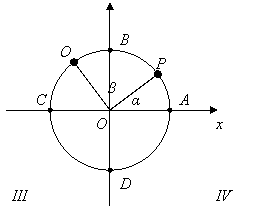
Per trovare le
coordinate polari del punto P la calcolatrice da come angolo l'angolo
α, mentre per convenzione l'angolo da utilizzare è l'angolo
β perché le misurazioni sono convenzionalmente in senso antiorario
rispetto all'asse delle ascisse
Trovare le coordinate polari di P(-3;4)
|
|
- Un vettore è caratterizzato da INTESITÁ DIREZIONE e VERSO.
- Coordinate polari
di un vettore 
:
b=3 α=35°
- Coordinate
sectiunesiane: si ottengo con 
- Per rappresentare completamente in forma sectiunesiana si introducono i VERSORI DEGLI ASSI CARTESIANI
essi hanno valore unitario ed
intensità 1
O
È
stato precedentemente detto che la posizione di un punto è individuata
da un vettore applicato nell'origine del sistema di riferimento: 
oppure si assegnano S ed α.
Se il corpo è in movimento la sua posizione dipende dal tempo:
Lo spostamento nell'intervallo di tempo (Δt=t2-t1) è:
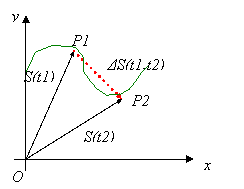
N.B. Lo spostamento non coincide con la traiettoria (linea verde)
La velocità media nell'intervallo di tempo (Δt=t2-t1) è:
La velocità media è una grandezza vettoriale parallela ed equiversa allo spostamento.
La velocità istantanea è la velocità media nel minor intervallo di tempo.
Se Δtà à=tende) lo spostamento tende a lunghezza nulla e alla direzione individuata dalla tangente della traiettoria.
La velocità istantanea è rappresentabile sulla traiettoria come una freccia che è tangente alla traiettoria ed ha lo stesso verso della curva. La prova che le velocità sono tangenziali si ha quando si fa roteare un corpo e si lascia la corda: PARTE PER LA TANGENTE.
La velocità istantanea è sempre tangenziale
Lorenzo Golfieri III C Liceo scientifico statale "Galileo
Galilei" Erba (CO) TRAIETTORIA NEL PIANO
y
x
Vm
La velocità media è parallela e quando lo spazio
diminuisce diventa velocità istantanea seguendo lo stesso verso
|
Privacy
|
© ePerTutti.com : tutti i diritti riservati
:::::
Condizioni Generali - Invia - Contatta
