| fisica |
|
ESPERIENZA N° 2: MISURA INDICE DI RIFRAZIONE DI UN SOLIDO - SPETTROMETRO A PRISMA
OBIETTIVO:
Misura dell'indice di rifrazione di un prisma di vetro crown.
STRUMENTI :
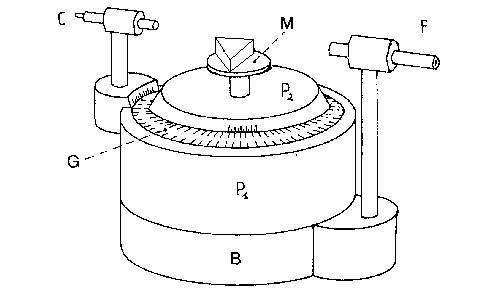
N° 1 Spettrometro. Lo spettrometro è costituito da una base fissa
B (vedi . 11.1) sul cui bordo superiore è incisa una scala
goniometrica G. Un collimatore F è solidale con la base mentre il
cannocchiale C è solidale con la piattaforma girevole P1. Una
seconda piattaforma girevole P2 costituisce la base di appoggio del
prisma. Entrambe le piattaforme ruotano attorno allo stesso asse (normale alla
base) passante per i centri delle due piattaforme. Sulle due piattaforme sono
incisi quattro nonii (due a due contrapposti) che consentono la determinazione
della posizione angolare sia del cannocchiale che della piattaforma P2
con un'approssimazione intorno alla trentina di secondi di grado. La lettura
dei nonii è facilitata dall'uso di un oculare. Il collimatore è
costituito da un tubo che porta alle estremità una fenditura verticale
regolabile in ampiezza (illuminata dalla luce prescelta) e posizionabile lungo
l'asse del collimatore (entro 1 o
N° 1 Prisma di vetro crown poggiato su M;
N° 1 Lampada al sodio.
INTRODUZIONE TEORICA:
L'indice di rifrazione di un mezzo è
definito come ![]() ,
dove c è la velocità
della luce nel vuoto e n è quella nel
mezzo.
,
dove c è la velocità
della luce nel vuoto e n è quella nel
mezzo.
Possiamo definire l'indice di rifrazione, partendo dalla legge di Snell:
![]()
dove n2,1 è detto indice di rifrazione relativo e gli n rappresentano gli indici di rifrazione dei mezzi.
Nel caso in cui il primo mezzo sia aria (cioè n1 = 1) si ha che n2,1 = n2. Tale indice dipende dalla lunghezza d'onda solo per le frequenze nel campo del visibile ( 3,8 * 1014 Hz £ n £ 7,9 * 1014 Hz ). Il fenomeno della dipendenza dell'indice di rifrazione della lunghezza d'onda incidente è detto dispersione. Consideriamo ora un particolare raggio trasmesso in cui:
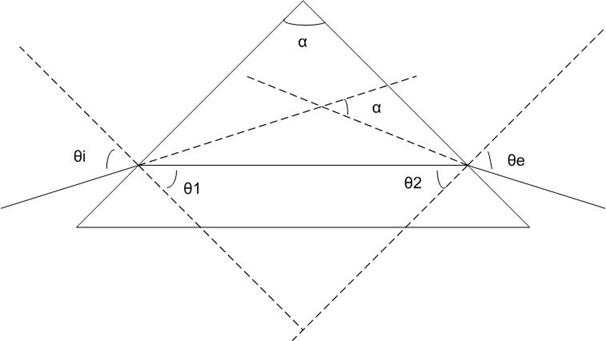
Ji = angolo di incidenza
J = angolo di prima rifrazione
J = angolo incidente nella seconda rifrazione
Je = angolo di seconda rifrazione
d = angolo di deviazione dovuto al prisma
a = angolo di apertura del prisma
Da semplici considerazioni geometriche si ha:
![]()
essendo a costante si ha anche che la somma di J e J è costante, indi:
![]()
inoltre per le relazioni fra angoli esterni e interni di un triangolo si ha:
![]()
quindi d varia al variare di qi ed è facile dimostrare che esiste un minimo per d qi) che si ottiene ponendo:
![]()
Ora consideriamo il prisma immerso nell'aria e applichiamo la legge di Snell:
1a faccia sinJi = nsinJ cosJidJi = ncosJ dJ
Þ
2a faccia sinJe=nsinJ cosJedJe = ncosJ dJ
ricordando che a J J e la condizione di minimo si ottiene dopo semplici passaggi:
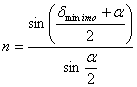
Solo in condizioni di deviazione minima l'indici di rifrazione dipende da a e da dminimo. In particolare se a è piccolo (£ 10°) si ha che:
dminimo =(n-l)* a
Parlando di errori, l'errore sull'indice di rifrazione si otterrà dalla proazione degli errori, e pertanto:
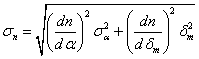
PROCEDIMENTO:
Prima di procedere nelle misurazioni delle grandezze, abbiamo visionato l'apparato a disposizione, cercando di comprendere le specifiche competenze degli elementi a disposizione.
A questo punto abbiamo:
Messo in bolla lo strumento: regolato il piano di giacitura del supporto dello spettrometro mediante due viti e indicatore a bolla;
Verificato la giacitura della piattaforma: regolata mediante due viti di livello in modo che le facce del prisma risultino parallele all'asse di rotazione della piattaforma;
Allineato il canocchiale ed il collimatore per mezzo della vite sotto il cannocchiale;
Accomodato il cannocchiale all'infinito ovvero mettendo a fuoco un oggetto lontano e regolando il tupo porta oculare rispetto al reticolo e bloccandolo una volta regolato;
Acceso la lampada al sodio, attendendo che si stabilisse e mettendola a contatto con la fenditura del collimatore;
Regolato l'immagine sulla fenditura, cercandolo con il cannocchiale e regolando la larghezza fenditura con vite finchè l'immagine coincide con il filo verticale del reticolo;
Posizionato il prisma sul supporto in modo che variandone l'altezza con le viti venisse ritrovata l'immagine della fenditura prodotta in trasmissione dal prisma.
Si è quindi proceduto alle misurazioni
vere e proprie: determinando l'angolo rifrangente ![]() del prisma sfruttando il processo di
riflessione sulle facce del prisma stesso.
del prisma sfruttando il processo di
riflessione sulle facce del prisma stesso.
Si è determinato l'angolo rifrangente ![]() del prisma seguendo due metodi:
del prisma seguendo due metodi:
Cannocchiale Fisso e Prisma Girevole;
Prisma Fisso e Cannocchiale Girevole.
Il primo metodo consiste nel ricavare l'angolo supplementare di ![]() mediante la differenza di due angoli misurati.
mediante la differenza di due angoli misurati.
Collocando il prisma sulla piattaforma abbiamo disposto il cannocchiale
in modo tale da formare con il collimatore un angolo acuto, quindi si è
fatta ruotare la piattaforma sino a quando non si è riusciti ad
individuare l'immagine della fenditura riflessa dalla faccia del prisma. Una
volta messo a fuoco e fatto ovviamente coincidere la riga di riferimento del
reticolo con con la riga gialla, si sono letti sulle scale del goniometro gli
angoli ![]() ed
ed ![]() .
.
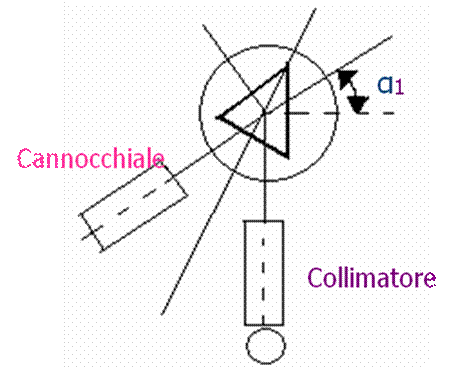
A questo punto dopo avere sbloccato la piattaforma e avendo cura di mantenere fisso il cannocchiale abbiamo ruotato la piattaforma stessa sino a quando il raggio riflesso dall'altra faccia del prisma fosse individuato dal cannocchiale, abbiamo così determinato gli angoli b e b bloccando nuovamente la piattaforma.
L'angolo cui si è fatta ruotare la piattaforma per individuare il raggio riflesso dalla seconda faccia del prisma per collimare l'immagine della fenditura è dato da:
![]()
Quindi la misura degli angoli b e b ed anche a e a permette di ottenere la stima di A secondo la relazione:
![]()
Dopo aver misurato l'angolo rifrangente ![]() con il metodo cannocchiale fisso e prisma
girevole abbiamo effettuato le misurazioni con il metodo Prisma Fisso e Cannocchiale
Girevole. Abbiamo effettuato nuovamente le operazioni di allineamento del
cannocchiale con il collimatore e posto la faccia opposta allo spigolo in modo
tale da renderla parallela al collimatore.
con il metodo cannocchiale fisso e prisma
girevole abbiamo effettuato le misurazioni con il metodo Prisma Fisso e Cannocchiale
Girevole. Abbiamo effettuato nuovamente le operazioni di allineamento del
cannocchiale con il collimatore e posto la faccia opposta allo spigolo in modo
tale da renderla parallela al collimatore.
Quindi, si è disposta la piattaforma in modo che l'angolo a d'apertura del prisma fosse rivolta verso il collimatore e la si è bloccata. In tal modo la riflessione del fascio di luce collimato avviene su entrambe le facce del prisma. Quindi ruotando il cannocchiale si sono cercati i due raggi riflessi e si è preso nota della loro posizione angolare.
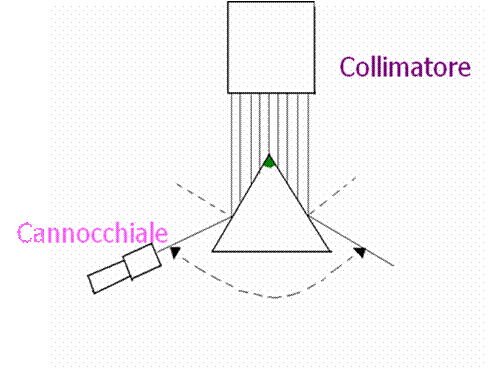
A questo punto ruotando in senso orario il cannocchiale, si è individuata la riga del fascio di luce riflessa corrispondente alla luce gialla; si è fatta coincidere la riga della luce gialla con la riga centrale del reticolo. Bloccato il Cannochiale si sono misurati gli gli angoli g ed g
Si è ruotato quindi il cannocchiale in senso antiorario e si è cercato il raggio riflesso dall'altra faccia del prisma ed una volta individuato si è fatta coincidere la linea centrale del reticolo dell'oculare con la linea gialla; bloccando il cannocchiale si sono annotati gli angoli f ed f . Dagli angoli appena ricavati si è assegnata una stima dell'angolo rifrangente A dalla relazione:
![]()
L'angolo di rifrazione risultante è la media pesata dei 2 risultati ottenuti con i 2 metodi appena descritti.
Dopo aver determinato l'angolo rifrangente ![]() del prisma, si è passati ad misurare
l'angolo di deviazione minima.
del prisma, si è passati ad misurare
l'angolo di deviazione minima.
Per il calcolo dell'angolo di deviazione minima abbiamo adoperato il seguente metodo.
Con il primo metodo si è posto il prisma sulla piattaforma e con
il cannocchiale si è cercata l'immagine rifratta della luce gialla. Nel
dettaglio posto il prisma sulla piattaforma in modo che l'angolo
di incidenza fosse molto grande e lasciando il cannocchiale e la
piattaforma liberi di ruotare, si è cercato con il cannocchiale il
raggio deviato. Muovendo la piattaforma si è diminuito l'angolo di
incidenza, di conseguenza la riga gialla si muoveva nel campo visivo
dell'oculare e la si è inseguita ruotando il cannocchiale. Si è
proceduto così per successivi spostamenti della piattaforma e del
cannocchiale finché pur procedendo nello stesso verso con la piattaforma, per
inseguire la riga gialla occorreva ruotare il cannocchiale in senso inverso: la
posizione in cui la riga gialla 'torna indietro' corrisponde alla
direzione dei raggi incidente ed emergente dove l'angolo di deviazione fra loro
è minimo. Una volta individuata, questa posizione è stata
raggiunta in modo più preciso con movimenti fini e si è presa
nota delle letture ![]() e
e ![]() .
.
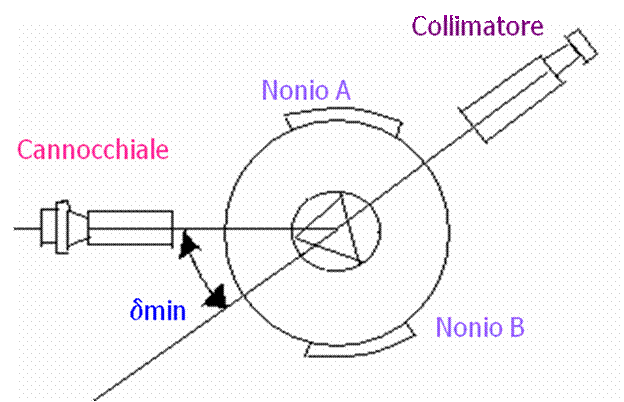
Abbiamo poi eliminato il prisma e puntato il cannocchiale nel
collimatore centrando la riga sul reticolo si leggono gli angoli ![]() e
e ![]() sui noni.
sui noni.
La deviazione minima è data da:
![]()
Abbiamo ripetuto le operazione per le altre righe associate ai colori viola e verde.
ANALISI DEI DATI:
I valori di dmin, per i rispettivi
colori, si sono calcolati facendo una media aritmetica fra i due valori
determinati con i noni A e B. A ciascuna misura si è attributo un errore
pari alla precisione dello strumento (0.5° * 1/30). Tale errore è stato
aumentato di
Stesso procedimento è stato usato per determinare a ed il relativo errore in entrambi i metodi. Si sono così attribuiti i due valori:
E' stata calcolata la media aritmetica fra i due valori ottenendo:
a
Infine si è calcolato l'indice di
rifrazione, si è evidenziato un indice per il giallo pari a 1.518
L'errore su n si è calcolato proando quello su a e dmin. ovvero, partendo dalla formula
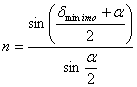
e sostituendo nella formula di proazione degli errori, abbiamo ottenuto:
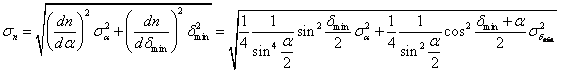
Misura di α |
|||||
|
|
|||||
|
1° Metodo |
|||||
|
Angolo |
a |
a |
b |
b |
|
|
Valore |
|
|
|
|
|
|
|
|||||
|
2° Metodo |
|||||
|
Angolo |
g |
g |
f |
f |
|
|
Valore |
|
|
|
|
|
|
Misura di dminimo |
|||||
|
1° Metodo |
|||||
|
|
J |
J |
s |
s |
dminimo |
|
Viola |
|
|
|
|
|
|
Giallo |
|
|
|
|
|
|
Verde |
|
|
|
|
|
|
|
|||||
|
2° Metodo |
|||||
|
|
J |
J |
J |
J |
dminimo |
|
Viola |
|
|
|
|
|
|
Giallo |
|
|
|
|
|
|
Verde |
|
|
|
|
|
|
Privacy
|
© ePerTutti.com : tutti i diritti riservati
:::::
Condizioni Generali - Invia - Contatta