| fisica |
|
Moto armonico semplice (M.A.S.)
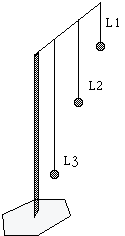
In laboratorio abbiamo osservato il movimento di un'asticella e per verificare che oscillava in moto armonico semplice abbiamo utilizzato il pendolo. Ricorrendo ad un proiettore siamo riusciti a vedere l' ombra dell'asticella proiettata sulla lavagna e fatto oscillare il pendolo contemporaneamente, abbiamo osservato che questi sono all'incirca in sincronia.
I dati sperimentali affermano quanto detto:
|
l (m) |
n. oscillazioni |
T (sec) |
|
l(asticella)= 0.73 |
|
|
|
l(pendolo)= 0.64 |
|
|
A causa del macchinario i periodi di oscillazione non coincidono perfettamente.
In laboratorio abbiamo verificato le osservazioni fatte in classe sulle proprietà del pendolo:
Indipendenza dalla massa
Isocronismo delle piccole oscillazioni
Dipendenza dalla radice quadrata di l
I parte:
Materiali e strumenti:
pendolo
cronometro (s: 0,001 sec)
varie masse
Abbiamo fatto oscillare il pendolo e tramite il cronometro, calcolato
sperimentalmente il periodo di oscillazione,sospendendo palline
di diverso materiale ma con lo stesso volume.
|
Massa(g) |
n. oscillazioni |
T (sec) |
|
Piombo: 92,6g |
|
|
|
Alluminio: 22,4g |
|
|
|
Ottone: 67,8g |
|
|
Questi dati sperimentali del periodo,(ottenuti facendo la media aritmetica di vari tempi!) ci dimostrano le ipotesi fatte: al variare della massa il periodo del pendolo non varia.
![]() Dalla formula del periodo del pendolo semplice
Dalla formula del periodo del pendolo semplice
abbiamo controllato se i dati sperimentali concordano
con quelli teorici.
|
l (m) |
T teor.(sec) |
T sper.(sec) |
e% |
|
|
|
|
|
II parte:
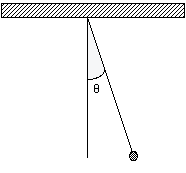
Calcolo dell' angolo di oscillazione del pendolo.
Al variare dell'angolo di oscillazione il periodo del pendolo non varia.
 III parte:
III parte:
Materiali e strumenti:
pendolo
cronometro (s: 0,001 sec)
una massa
metro (s: 0,001mm)
Abbiamo fatto oscillare il pendolo con lunghezze diverse,
calcolando sperimentalmente il periodo di 10 oscillazioni
|
l (m) |
T sec) |
|
l1= 2,0 |
|
|
l2= 1,20 |
|
|
l3= 0,40 |
|
|
|
|
|
Possiamo osservare che al variare della lunghezza del filo, il periodo del pendolo varia.
![]()
![]()
à
Abbiamo preso una corda con appesa una massa e l'abbiamo fatta oscillare, tramite il cronometro abbiamo calcolato sperimentalmente il periodo di oscillazione e successivamente determinato, tramite la formula, il valore dell'accelerazione di gravità.
o
![]()
![]()
![]()
F2
![]() F1
F1
m
mg
|
l(m) |
n. oscillazioni |
T (sec) |
g (m/s2) |
e% |
|
|
|
|
|
|
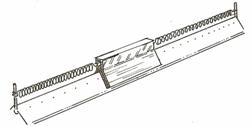
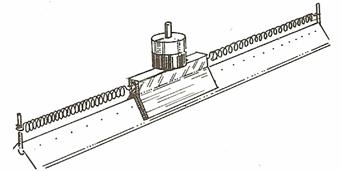
E' possibile eseguire l'esperimento con la rotaia a cuscino d'aria, sistemando il carrello al centro della rotaia e agganciandolo alle due estremità della rotaia mediante due molle.
Messa in funzione la rotaia,abbiamo spinto lateralmente il carrello,lasciandolo poi libero oscillare.
Abbiamo preso nota del
periodo di oscillazione e lo abbiamo moltiplicato per
|
l(m) |
T (sec) |
n. oscillazioni |
|
|
|
|
All' esperimento della rotaia abbiamo aggiunto alcune masse, provocando una diminuzione della velocità delle oscillazioni.
|
Mtot.(g) |
T(s) |
K (N/m) |
|
|
|
|
![]()
Il k calcolato si riferisce alle due molle agganciate alla rotaia, il k di una sola molla corrisponde precisamente alla metà del risultato trovato, pertanto:
![]()
Per trovare questo k, abbiamo agganciato la molla ad un sostegno e successivamente appese varie massa a questa.
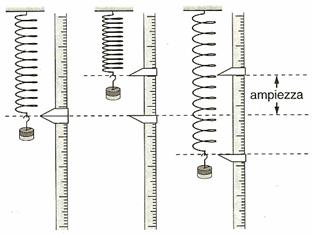
Lunghezza
molla =
|
M (g) |
Ampiezza(cm) |
K(N/m) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Da questi dati in tabella possiamo capire che la costante elastica della molla calcolata tramite la formula non corrisponde ai dati sperimentalmente trovati, in quanto la forza di gravità condiziona
i risultati. Quindi dovremmo posizionare la molla sulla rotaia in orizzontale e aggiungere le masse, in quanto la forza di gravità in questo caso inciderebbe meno ed avremmo risultati molto più precisi.
|
M(g) |
T(s) |
|
|
|
Rapporto col periodo e massa precedente:
![]()
![]()
![]()
|
Privacy
|
© ePerTutti.com : tutti i diritti riservati
:::::
Condizioni Generali - Invia - Contatta