VISCOSITÀ E PORTATA DI UN TUBO REALE

VISCOSITÀ E PORTATA DI UN TUBO REALE

Entro un liquido perfetto in movimento consideriamo, ad un generico istante "t", una linea chiusa "l"; e consideriamo l'insieme delle linee di flusso che all'istante considerato si appoggiano sulla linea "l". Nel loro insieme queste linee, costituiscono quello che si chiama: "un tubo di flusso". Per la definizione stessa di linea di flusso in ogni punto della superficie laterale del tubo di flusso la velocità del fluido risulta, all'istante considerato, tangente alla linea e dunque al tubo di flusso stesso: essendo nulla la componente della velocità del fluido ortogonalmente alla superficie laterale del tubo di flusso, questo si comporta come un tubo impermeabile, attraverso la cui superficie laterale non fluisce alcun liquido. Consideriamo la porzione di tubo di flusso compresa, all'istante considerato, fra la sua sezione "S" ed un'altra sezione qualunque "S' ".

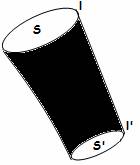
Tubo elementare di flusso

Supponiamo che il tubo abbia sezione "S" abbastanza piccola perché in ogni punto di essa la velocità del fluido sia la stessa, si dice allora che si tratta di un tubo elementare di flusso, e supponiamo che S sia ovunque ortogonale alla velocità. Supponiamo che anche "S' " sia una sezione normale. Se a partire da "t" consideriamo un intervallo infinitesimo di tempo "dt", la massa di fluido che fluisce in "dt" attraverso la sezione "S" sarà evidentemente data da:

dm = dV = Svdt

Infatti, il volume "dV" di fluido che attraversa "S" nel tempo "dt" è paria dV = Svdt, ossia base "S" per altezza vdt. Nello stesso intervallo di tempo "dt", attraverso la sezione "S' " passerà la quantità di massa dm = dV' = S'v'dt; ma, essendo il fluido incompressibile ed essendo le superfici laterali del tubo di flusso impermeabili, la massa "dm" entrata nel tubo deve essere pari alla massa "dm' " che ne è uscita; da cui:

Sv = S'v'

La quantità "Sv", che rappresenta il volume che passa nell'unità di tempo attraverso una sezione del tubo di flusso, si dice portata volumica "Q", e nel sistema SI si misura in m /s; scriveremo pertanto:

Q = Sv = invariante

Quest'ultima prende il nome di: "equazione di continuità". Istante per istante, la portata volumica è la stessa attraverso tutte le sezioni di uno stesso tubo di flusso. Se il moto avviene in regime stazionario, la portata "Q" è naturalmente anche

indipendente dal tempo. L'invarianza della portata implica che, laddove un tubo di flusso si

restringe, graficamente le linee di flusso necessariamente si addensano, dando così naturale realizzazione della convenzione secondo cui la velocità del fluido risulta rappresentata dal numero di linee di flusso per unità di area della sezione normale.