Le funzioni economiche e Costi

Le funzioni economiche e Costi

Cos'è una funzione economica?

Le funzioni economiche sono delle funzioni che rappresentano l'andamento economico diun bene sul mercato, esse sono le funzioni di domanda, offerta, costo totale, costo marginale, costo unitario, ricavo e utile.

Il modello matematico

Il modello matematico è un modello che rappresenta la realtà attraverso una funzione matematica che dovrà essere massimizzata o minimizzata e che dovrà rispettare dei vincoli di segno, tutte le funzioni sono studiate nell'intervallo x>=0, e dei vincoli tecnici, come ad esempio la massima capacità produttiva o le ore massime di lavoro ecc..

Costi di produzione

Il costo totale (Ct(x)) è uguale alla somma dei costi fissi e dei costi variabili, ed è funzione della quantità x di merce prodotta.

I costi fissi (C_f) indicano tutti quei costi il cui ammontare è indipendente dalla quantità prodotta, ad esempio: stipendi del personale amministrativo; ammortamento dei macchinari; spese per il deperimento e le riparazioni degli edifici; ecc.

I costi fissi geometricamente sono rappresentati da una semiretta parallela all'asse delle ascisse:

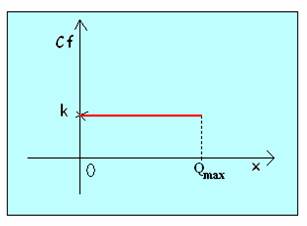
Essendo i costi fissi costanti possiamo scrivere una equazione del tipo:    

Costi fissi = costante

ovvero:

Cf  = k

Se indichiamo con C_f  i costi fissi e con k una costante espressa in Euro.

Da notare che anche se le quantità prodotte sono nulle i costi fissi non sono nulli, ma sono uguali a k.

I costi variabili (C_v(x)), invece, si hanno quando esiste una proporzionalità diretta tra costo complessivo e quantità prodotta, essi comprendono: i costi per l'acquisto di materie prime; i costi del lavoro diretto; le spese correnti relative al capitale fisso, quali combustibile, riparazioni ordinarie e mantenimento.

I costi variabili geometricamente si rappresentano con una S rovesciata, forma che riflette la legge delle proporzioni variabili:

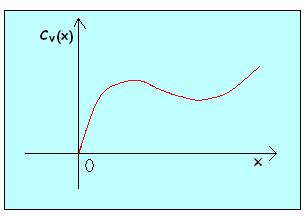
Nelle fasi iniziali di produzione con un dato impianto, all'aumentare dell'impiego del fattore variabile aumenta la produttività e quindi il costo variabile medio diminuisce. Questa situazione continua fino a che non viene raggiunta la combinazione ottimale dei fattori fissi e variabili. Oltre questo punto la produttività del fattore variabile diminuisce e il costo variabile medio aumenta.

Pertanto il Costo Totale è espresso dalla funzione:

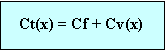
E si rappresenta:

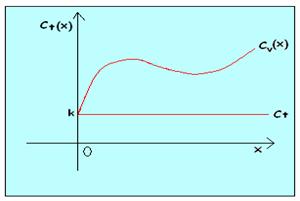
Per l'analisi dei costi di produzione si definiscono altre due funzioni: il costo medio e il costo marginale.

Il costo medio è dato dal rapporto tra il costo totale per produrre la quantità x e la quantità x prodotta.

Esso può trovarsi in due forme:

lineare Cm(x) = Ct(x) = ax+b = a +  b

x   x x

quadratica Cm(x) = Ct(x) = ax² + bx + c =  ax + b + c

x    x x

Il costo marginale può essere definito nel campo discreto e nel campo continuo.

Si definisce costo marginale nel campo discreto il costo sostenuto per ottenere un'unità addizionale di prodotto, calcolandola sul rapporto incrementale tra l'incremento del costo e l'incremento della quantità prodotta.

Si definisce costo marginale nel campo continuo la derivata della funzione del costo totale rispetto alla quantità prodotta. In generale, il Cma ha lo stesso andamento del Cm: inizialmente decresce e successivamente cresce. Cm e Cma coincidono nel punto in cui il Cm è minimo:

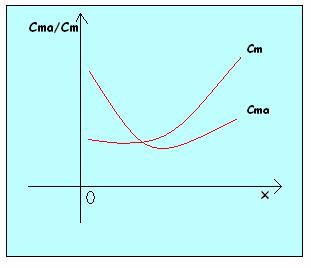
Cm = Ct(x)

x

Cm' =  Ct'(x) - 1 ∙ Ct(x)

x²

Ct'(x) - 1 ∙ Ct(x) = 0

x²

Ct'(x) - 1 ∙ Ct(x)   = 0

x²

Ct'(x) ∙ x   = Ct(x)

x x

Cma = Cm