ALBERI E ALBERI BINARI DI RICERCA (BST) - Albero pieno

ALBERI E ALBERI BINARI DI RICERCA (BST)

Definizione

Si definisce albero una struttura dati costituita da un insieme finito di nodi tali che:

Esiste un nodo speciale chiamato radice (root);

I restanti nodi sono suddivisi in n insiemi disgiunti T₀, T₁,,T_n-l ciascuno dei quali è un albero.

Esempio

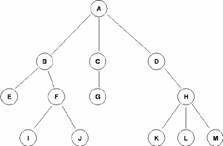
Glossario

Nodo  Ramo

Grado di un nodo   Grado di un albero

Foglia Padre

lio Fratelli

Livello Altezza o profondità

Alberi binari

Noi tratteremo solo alberi binari!

Si definisce albero binario un insieme (anche vuoto) formato da un nodo radice e da due alberi binari disgiunti detti sottoalbero sinistro e sottoalbero destro

Piú semplicemente un albero binario è un albero avente grado 2

Numero massimo di nodi per livello

In un albero binario il numero massimo dei nodi di livello i è pari a 2^i-l con i>=1:

Si dimostra per induzione su i. Infatti per la radice è immediato. Dato che ogni nodo può avere al  massimo due li per il livello i il numero massimo dei nodi è pari a 2 volte il numero massimo di nodi del livello i-l

Numero massimo nodi per albero

Il numero massimo di nodi di un albero di profondità k è 2^k-l con k>=1:

Albero pieno

Un albero di profondità k si dice pieno quando è formato da 2^k-l nodi

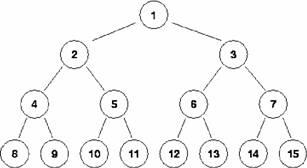
Albero binario:rappresentazione collegata

In C/C++ è possibile rappresentare un albero binario mediante una rappresentazione collegata:

struct nodo

struct nodo *radice=NULL;

Attraversamento di un albero

Una delle operazioni piú comuni è la visita di tutti i nodi dell'albero. 4 possibilità:

Inorder (SVD);

Postorder (SDV);

Preorder (VSD);

Di livello (richiede l'utilizzo di una coda).

Vedere nel codice di esempio anche le operazioni di copia e controllo equivalenza!

Alberi binari di ricerca (BST)

Un albero binario si definisce albero binario di ricerca se:

Ogni nodo è caratterizzato da una chiave univoca;

Per ogni nodo le chiavi dei nodi appartenenti al sottoalbero di destra sono piú grandi di quella del padre

Per ogni nodo e chiavi dei nodi appartenenti al sottoalbero di sinistra sono piú piccole di quella del padre

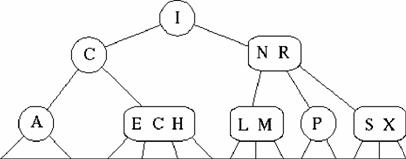
Esempio di Binary Search Tree

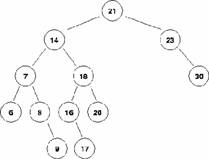
Albero binario di ricerca:rappresentazione collegata

Nel caso dei BST è opportuna una rappresentazione piú mnemonica:

struct nodo

struct nodo *radice=NULL;

BST: operazioni specifiche

Le operazioni viste per gli alberi binari sono valide anche per i BST ad eccezione dell'equivalenza.

Operazioni specifiche (vedere codice):

inserimento

cancellazione

ricerca

selezione

Inserimento in foglia

È il piú semplice

Adatto ad essere implementato sia ricorsivamente che iterativamente

Si traversa l'albero confrontando la chiave del nodo da inserire con la chiave del nodo che si sta visitando e ci si sposta di conseguenza.

Se non c'è il lio inserisco.

Inserimento in radice

Nei casi reali è frequente che l'elemento ricercato sia fra quelli piú recentemente inseriti.

Inserimento in foglia svantaggioso!

Rotazioni

L'inserimento in radice è complesso e richiede l'utilizzo di modifiche strutturali all'albero dette rotazioni

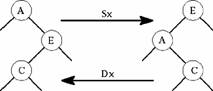
Esempio di inserimento in radice

Per inserire in radice si effettua un inserimento in foglia seguito da rotazioni per riportare l'elemento verso l'alto

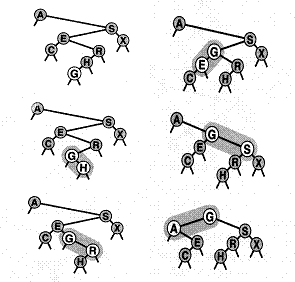
Inserimento in radice: crescita

Crescita di un albero in cui vengono inseriti in radice gli elementi A, S, E, R, C e H:

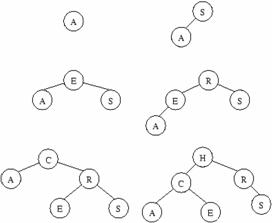
Cancellazione di un nodo

Operazione complessa, 3 possibilità:

foglia: semplicemente elimino.

nodo con solo un lio: elimino e collego al padre l'unico lio.

nodo con due li: lo elimino e lo sostituisco con l'elemento avente chiave maggiore fra quelli del sottoalbero dei nodi con chiave minore (grado sempre <=1).

Ricerca

Analoga all'inserimento in foglia.

Il numero di passi necessario per trovare il nodo avente la chiave ricercata è legato alla profondità dell'albero.

In un albero pieno questa è log₂n con n numero dei nodi

Nel caso peggiore può essere n!

Albero degenere

L'inserimento di nodi ordinati può portare a situazioni degeneri

Situazione frequente!

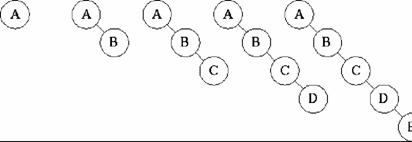
Inserimento casuale

Una possibile soluzione alla creazione di alberi degeneri è mescolare inserimento in foglia e inserimento in radice.

Inserimento casuale

L'inserimento casuale riduce i problemi ma non li risolve completamente.

Selezione di un nodo

Se considero i nodi ordinati secondo la chiave posso immaginarli come numerati da 0 a n.

La selezione è l'operazione che mi permette dato un indice k di recuperare il nodo corrispondente.

Si contano i nodi di uno dei sottoalberi e ci si sposta di conseguenza

Partizione di un BST

La partizione di un albero binario di ricerca consiste nel portare in radice il nodo di indice desiderato

Se k è l'indice del nodo in radice il sottoalbero di sinistra contiene k nodi e il sottoalbero di destra n-k

Combinazione di selezioni e rotazioni

Bilanciamento di un BST

Il partizionamento permette di bilanciare un albero partizionando ricorsivamente tramite l'elemento di mezzo.

Soluzione onerosa (O(n))

Non adeguato in tutte le condizioni

Alberi AVL

Un albero si dice bilanciato quando i due sottoalberi della radice hanno un differenza di profondità <=1 e sono a loro volta bilanciati.

Gli alberi AVL sono alberi le cui operazioni di inserimento mantengono l'albero bilanciato.

Inserimento in foglia con rotazioni che bilanciano

Inserimento in alberi AVL

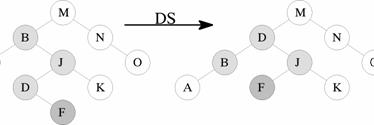
4 tipi di rotazione SS, DD, SD, DS:

Alberi 2-3-4

Gli alberi 2-3-4 sono alberi di ricerca NON binari aventi 3 tipi di nodi:

nodi 2: analoghi a quelli dei BST.

nodi 3: tre li e due chiavi, i valori delle chiavi dei sottoalberi sono suddivisi in funzione delle chiavi del padre.

nodi 4: quattro li e tre chiavi,

Alberi 2-3-4: esempio

Gli alberi 2-3-4 possono essere perfettamente bilanciati

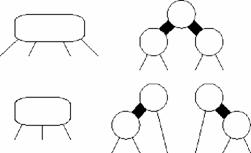
Alberi rosso-neri

La complessità di gestione degli alberi 2-3-4 può essere ridotta introducendo collegamenti colorati: