ANALISI DEL SISTEMA SERIE - ANALISI DEL SISTEMA PARALLELO

5.3 ANALISI DEL SISTEMA SERIE

Effettuiamo l'analisi del sistema serie. Con la terminologia introdotta in precedenza, considerati gli eventi: S= e C_j= si ha:

1)

Applicando il teorema di De Morgan, si ha:

    2)

La relazione (2), può essere espressa dicendo che il sistema non funziona se e solo se non funziona almeno uno dei suoi componenti.

L'affidabilità del sistema R = P(S) è dunque data da:

R = 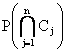3)

Inutile ripetere che la struttura "serie" è definita dalla (1), o equivalentemente dalla (2) e non dalla (3) (che è solo un modo di calcolare l'affidabilità).

Analogamente, detta F l'inaffidabilità del sistema, si ha:

   4)

Dalle proprietà elementari del calcolo delle probabilità si ricava che:

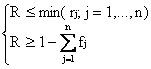5)

dove, si ricorda, r_j = P(C_j) e . Le disuguaglianze di cui sopra sono sempre valide, e sono in particolare utili quando gli eventi non sono indipendenti (o non si hanno informazioni sulla loro dipendenza).

Se i componenti del sistema sono indipendenti, le relazioni precedenti diventano:

   e 6)

Quest'ultima relazione approssimata vale se le f_j sono abbastanza piccole, ossia se i componenti sono - come spesso accade nella pratica - di elevata affidabilità; essa è detta - per ovvi motivi - "approssimazione degli eventi rari" (ed indipendenti). Essa si ricava dalla formula generale della probabilità dell'unione di più eventi.

Esempio Si considerino due componenti indipendenti in serie, di affidabilità pari a r = 0.99. L'affidabilità del sistema sarà pari a R = r² = (0.99)² = 0.9801. Quindi F = 1-R = 0.0199. se si utilizza l'approssimazione della 6) per F, si ha F' = 2f = 2(0.01) = 0.02, risultato praticamente uguale a quello esatto ( comporta un errore percentuale dello 0.5%).

Se i componenti hanno tutti la stessa affidabilità [P(C_j) = r, j =1, , n] , si ottiene:

R = rⁿ    7)

Tale relazione - essendo r < 1 - mostra come R diminuisca molto rapidamente al crescere del numero n di componenti. Ciò è illustrato dal diagramma seguente, in cui R è riportata in funzione di n (per comodità mediante delle curve continue; ma si noti che n è un numero intero), al variare di r. Gli andamenti sono simili a quelli di un esponenziale decrescente, come si può dedurre dalla relazione: R = rⁿ = exp[-n∙|log(r)|]. Naturalmente, R aumenta con r.

Si osservi che ( se f è sufficientemente piccolo). Ecco perché, per r prossimo ad

1, le curve sono approssimativamente delle rette decrescenti in n.

La 6) è la particolare funzione di affidabilità del sistema, ovvero la relazione tra R e le affidabilità dei singoli componenti:

= F(r₁, r₂, , r_n)

La funzione F gode delle proprietà dei sistemi coerenti:

F

F

.

Esempio. Si consideri un sistema serie costituito da 200 componenti indipendenti tutti uguali tra di loro. Quale deve essere l'affidabilità minima r di ogni singolo componente affinché l'affidabilità R_S del sistema si superiore al 99%? Si ha:

affinché l'affidabilità del sistema sia superiore al 99%, l'affidabilità di ogni singolo componente deve essere superiore a 0.99995 (essendo R crescente con r). Ciò mostra come l'affidabilità del sistema serie sia molto inferiore all'affidabilità dei singoli componenti, se questi sono numerosi

Ad esempio, collegando 100 componenti di affidabilità pari a r= 0.99, si ha una affidabilità R per il sistema serie pari a 0.366!. Si nota che questo risultato è equivalente al seguente: "Dato un sistema qualsiasi - non necessariamente serie - i cui componenti hanno (in un dato intervallo di tempo) affidabilità pari al 99%, la probabilità che nessuno di essi si guasti in tale intervallo è pari al 36.6%."

5.4 ANALISI DEL SISTEMA PARALLELO

Un sistema si dice parallelo quando funziona se almeno uno dei suoi componenti funziona. Utilizzando la solita simbologia del caso precedente, si ha:

(1)

Applicando il teorema di De Morgan, si ha:

(2)

La (2) può essere espressa dicendo che il sistema non funziona solo se non funziona nessuno dei suoi componenti. Si ha:

R = 3)

    4)

Analogamente: 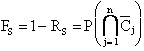   5)

Se i componenti del sistema sono indipendenti, è conveniente calcolare l'affidabilità del sistema in funzione dell'inaffidabilità dei singoli componenti::

   e 6)

Se i componenti hanno tutti la stessa affidabilità [P(C_j) = r j =1, , n] , si ottiene:

   7)

Esempio. Si considerino ancora due componenti di affidabilità pari a r=0.99, ma stavolta collegati in parallelo. L'affidabilità del sistema sarà pari a R = 2r - r² = 2(0.99) - (0.99)² = 0.9999. Oppure, più semplicemente, F = f² = (0.01)² = 0.0001 = 1E-4, da cui R=0.9999. Si ha dunque un incremento di affidabilità, che in termini percentuali è pari all'1%.

Se si aggiunge un altro componente in parallelo, si ha F = f³ = (0.01) ³ = 1E-6, ovvero: R = 0.999999 (verificare l'esattezza del risultato anche mediante il calcolo di R con la probabilità dell'unione): tali numeri dimostrano che, per sistemi formati da componenti di elevata affidabilità, è conveniente esprimerne le prestazioni mediante l'inaffidabilità, anziché l'affidabilità. Nell'aggiunta del terzo componente, si ha un incremento di affidabilità (rispetto al caso con due componenti) pari allo 0.0099%, molto inferiore a quello precedente. Si tratta di un risultato di carattere generale, discusso nel seguito.

Dalla 7) si vede, come intuitivo, che R aumenta molto rapidamente con n, tendendo asintoticamente ad 1 al divergere di n, come anticipato e come verificato nel precedente esempio. Diagrammando tale relazione in funzione di n, otteniamo il grafico in ura:

Anche per il sistema parallelo possiamo introdurre la funzione di affidabilità:

F(r₁, r₂, , r_n) =1-, che gode delle solite proprietà:

F(0,0,., 0) = 0;

F

.

Incrementi di affidabilità conseguibili con il parallelo. Si consideri un sistema costituito da (n-l) componenti uguali in parallelo, indipendenti, di affidabilità r; aggiungendo un altro componente in parallelo ai primi, l'affidabilità del sistema cresce. Si può facilmente verificare che l'incremento di affidabilità DR(n) = R(n) - R(n-l) è pari a , quantità positiva. Tale funzione è però decrescente in n, e tanto più rapidamente quanto più r è prossimo ad 1(vedi esempio precedente); in particolare anche l'incremento percentuale di affidabilità , decresce fortemente al crescere di n, come mostrato in ura.

Ciò può essere visualizzato anche sulle curve della affidabilità in funzione di n R(n) (v. curva superiore in ura), che sono di tipo "concavo".

Detto a parole, aggiungendo componenti in parallelo ad un sistema, si riesce ad aumentare l'affidabilità di un quantità sempre più piccola fino ad un valore praticamente non apprezzabile in termini percentuali. E' chiaro che esisterà un numero ottimale di componenti da mettere in parallelo, ricavabile da un compromesso tra l'affidabilità di un sistema (quindi indirettamente tra i costi del guasto), e i costi derivati dall'installazione dei componenti che crescono linearmente con n. Naturalmente, l'inserzione di componenti in parallelo è il metodo più semplice per aumentare l'affidabilità del sistema, ed è quindi - come anticipato - utilizzato in fase di progetto. Di seguito si dà un esempio numerico di ciò.

Esempio. Si ha a disposizione un insieme di componenti identici aventi affidabilità = 0.70. Si vuole ottenere un sistema di affidabilità = 0. 999 o più. Quale è il (minimo) numero di tali componenti da porre in parallelo?.

Basta imporre la disuguaglianza: F = fⁿ = (0.30) ⁿ < 0.001, da cui n >5.74; quindi, è necessario collegare almeno 6 componenti in parallelo per ottenere l'affidabilità desiderata.

5.5 SISTEMI SERIE - PARALLELO

Spesso i sistemi sono decomponibili in più sottosistemi di tipo "serie" e /o "parallelo", collegati tra di loro ancora secondo tali tipi di strutture. Tali sistemi, detti appunto "serie-parallelo", sono facilmente risolubili mediante successive "riduzioni" a sistemi più semplici. Nel caso di componenti indipendenti (che assumiamo salvo avviso contrario), è facile vedere che anche i sottosistemi che si ottengono mediante le riduzioni sono indipendenti tra di loro.

Un esempio elementare è fornito di seguito.

Esempio 1. Consideriamo il sistema indicato in ura, destinato ad alimentare un carico w pari a 100 MW (questo può essere il valore assunto costante della potenza attiva richiesta, oppure - più comunemente - il valore di picco del carico nell'intervallo di tempo a cui è relativo il calcolo dell'affidabilità). Le capacità di generatori e linee sono date da: c(g₁)=c(g₂)=c(l₁)=c(l₂)= 180 MW;

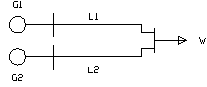
Si vuol calcolare l'affidabilità del sistema in un anno, supponendo che le inaffidabilità dei componenti par tale periodo risultino pari a: q_g1 = q_g2 =0.05 e q_l1 = q_l2 = 0.02.

Il sistema funziona se almeno un sottoinsieme (generatore + linea) funziona, quindi esso è equivalente al parallelo dei sottosistemi A (G₁,L₁) e B(G₂,L₂); ognuno di tali sottosistemi è costituito dalla serie di generatore e linea, in quanto entrambi devono funzionare perché il sottosistema possa - da solo - alimentare il carico. Inoltre, non è difficile verificare che tali sottosistemi sono indipendenti (verificarlo per esercizio).

L'affidabilità del sistema in un anno è allora data da:

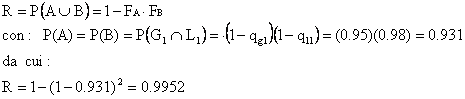
Anche in questo caso, l'affidabilità del sistema è superiore a quella di ogni singolo componente (ma ciò non è vero sempre per un sistema serie-parallelo: provare a trovare un contro-esempio); il sistema considerato è detto "Parallelo di serie" (PS). E' interessante provare a confrontarlo con un sistema di tipo "Serie di parallelo" (SP), come nell'esempio che segue.

Esempio 2

Dati i sistemi A (di tipo "PS") e B (di tipo "SP") dire quale dei due è più affidabile, nell'ipotesi che tutti i componenti siano uguali e indipendenti e abbiano affidabilità r = 0.80.

Si ha:

;   

Il sistema SP è dunque più affidabile del sistema PS. Si può dimostrare, a partire dalle relazioni precedenti, che ciò è vero in generale (cioè per ogni valore di r in (0,1): provare a verificarlo); dunque, avendo a disposizione dei componenti da inserire in parallelo per migliorare l'affidabilità di una struttura serie, è preferibile "raddoppiare" i singoli componenti, anziché "raddoppiare" l'intero sistema, a parità di affidabilità dei componenti; provare a dare una giustificazione "intuitiva" di ciò.

Si noti altresì che - in generale - nessuna delle due strutture rappresenta necessariamente un miglioramento rispetto all'affidabilità del singolo componente.

5.6 SISTEMI DI TIPO "PARALLELO PARZIALE"

Un sistema parallelo parziale è un particolare sistema che funziona quando (se e solo se) funzionano almeno k degli n componenti che costituiscono il parallelo. Si considerino i seguenti eventi:

S= C_j=    G_i =; risulta:

ove ogni evento G_i è costituito da eventi rappresentanti tutte le possibili conurazioni in cui "i" elementi sono funzionanti, e gli altri (n-i) sono guasti. Come intuitivo tali eventi sono tra loro incompatibili, così pure gli n-k+1 eventi G_i; si può quindi scrivere che .

Nell'ipotesi di componenti indipendenti e di uguale affidabilità r, detta f la loro inaffidabilità, si può applicare la legge di distribuzione Binomiale, e si ha:

; 1)

Esempio: Calcolare l'affidabilità del sistema in ura, supponendo che i soli componenti che si possono guastare sono i generatori e che P(G_i) = p = 0.98. Si supponga che tutti i generatori siano indipendenti.

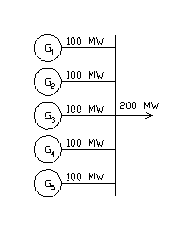Il sistema s funziona quando funziona almeno una coppia di generatori. In altre parole, il sistema funziona quando funzionano due, tre, quattro o cinque generatori (sistema "2 su 5").

L'affidabilità R_S è data dalla probabilità dell'unione di tutti i relativi eventi.

Da qui si ricava:

La formula può essere scritta in forma più compatta:

La R_S poteva essere ricavata anche - più semplicemente - a partire dall'inaffidabilità del sistema. Infatti, il sistema non funziona se si verifica uno dei due eventi:

a)    non funziona alcun generatore;

b)   funziona un solo generatore;

per cui,

(Nota: si noti che per effettuare tale calcolo non c'è bisogno di ricordare la formula della legge Binomiale, a differenza che per il calcolo di R!)

Da cui:

R_S = 1-F_S = 0.999999212

Come già notato, l'espressione in termini di F è di più semplice interpretazione (ci dice che - in media - il sistema si guasta circa 8 volte su 10 milioni di prove, senza obbligarci a contare una lunga sfilza di 9).

Si osservi che un sistema parallelo è un particolare sistema parallelo parziale, cioè è un sistema "1 su n". Dualmente, un sistema serie è un sistema "n su n". Verificare la veridicità di tali affermazioni particolarizzando le precedenti formule generali.

5.7 AFFIDABILITÀ DI SISTEMI COMPLESSI: IL METODO DELLA PROBABILITÀ TOTALE (o "DI   DECOMPOSIZIONE")

A volte, l'affidabilità di un sistema avente uno schema complesso - non immediatamente riducibile ad uno schema serie-parallelo - può essere calcolata condizionando l'affidabilità del sistema rispetto al guasto e al funzionamento di uno o più componenti del sistema stesso. In questo modo, il sistema si riduce a più sottosistemi semplici, dei quali può essere calcolata l'affidabilità con uno dei metodi noti.

Individuato un qualsiasi componente c, detto "critico", si può pensare di condizionare rispetto agli eventi C e , ottenendo, per il teorema della probabilità totale:

    1)

dove, per il significato di probabilità condizionata, P(S|C) è l'affidabilità del sottosistema che si ottiene "cortocircuitando" affidabilisticamente il componente c (ossia considerando l'evento "C" vero, e quindi c funzionante) e P(S|) è l'affidabilità del sottosistema che si ottiene considerando c guasto (ossia considerandolo un "circuito aperto" affidabilistico).

Si osservi che il metodo è applicato correttamente quando si condiziona rispetto ad eventi incompatibili ed esaustivi. Ad esempio, se nel sistema si individuano due componenti critici (c, d), si deve condizionare rispetto agli eventi

Se l'elemento critico è individuato in maniera opportuna (questo dipende dall'esperienza di chi effettua l'analisi: non ci sono regole generali!), i due sottosistemi "S|C" e "S|" (utilizziamo questa notazione per comodità: si ricorda che nel calcolo delle probabilità non sono definiti gli eventi condizionati, ma le probabilità condizionate) risultano di agevole risoluzione, e quindi il calcolo di P(S) si semplifica notevolmente. Un classico esempio di utilizzazione efficace di tale metodo è quello relativo alla analisi delle cosiddette strutture "a ponte", come di seguito illustrato. Si noti che nella applicazione di tale metodo è molto importante (nel senso che semplifica di molto i calcoli) l'ipotesi di indipendenza dei componenti (in tale ipotesi, sapere che c funzioni oppure no non altera la probabilità di funzionamento degli altri componenti: si fa notare che ciò non sempre è vero!).

Esempio: Sistema di tipo "ponte"

Consideriamo un sistema - detto per ovvi motivi di tipo "ponte" - il cui schema affidabilistico è riportato in ura. Tale schema rappresenta un sistema che funziona quando funziona almeno uno dei seguenti sottosistemi di tipo serie: (a,d), (b,e), (a,c,e), (b,c,d). Infatti ognuno di tali "percorsi" - se formato da componenti tutti funzionanti - assicura il collegamento ingresso-uscita.

Nella ipotesi (componente c guasto, ovvero blocco c "aperto") e in quella C (componente c funzionante, ovvero blocco c "cortocircuitato") la struttura del sistema diviene rispettivamente quella contrassegnata con A e quella contrassegnata con B. Il sistema A è un "parallelo di serie" (PS), mentre il sistema B è un sistema "serie di parallelo" (SP), strutture già considerate in precedenza. L'affidabilità della struttura a ponte risulta dunque essere combinazione lineare delle affidabilità, R_A = P(A) e R_B = P(B), delle due strutture semplici.

Nel caso di componenti indipendenti (si ricordi l'osservazione sulla indipendenza fatta più sopra), con uguale affidabilità p, si ha, come già visto:

;  2a)

(Nota: si noti che il metodo vale sempre, anche se i componenti non sono indipendenti; l'indipendenza è utile solo ai fini del calcolo!).

La funzione di affidabilità strutturale del sistema, quindi, vale:

R = (1- p) R_A + p R_B 2b)

Naturalmente, si ha R_A  < R < R_B (abbiamo già visto che un sistema "SP" è più affidabile del sistema "PS", a parità di p, e quindi, per ogni valore di p, si ha: R_A < R_B).

Ad esempio, nel caso: p = 0.80, si ha R = (1- 0.8) (0.8706) +(0.80)(0.9216) = 0.9114.

Dalle 2), volendo, si può ricavare la seguente espressione generale per l'affidabilità statica del ponte in funzione di p:

R = 2p² + 2p³ - 5p⁴ + 2p⁵   3)

Si noti che, naturalmente, nulla vieta di considerare un altro componente come "critico", senza particolari difficoltà. Lo si faccia per esercizio, tra l'altro molto istruttivo (anche per . l'Elettrotecnica).

E' facile controllare che, detta R(p) tale funzione, si verificano le solite proprietà:

1) R(0) = 0;   2) R(1) = 1 ; R(p) crescente in p (per 0<p<1).

Con analogo ragionamento, è possibile ricavare la funzione di inaffidabilità; in funzione di q = 1-p, essa risulta formalmente identica alla 3); si trova infatti:

Da queste relazioni è facile rendersi conto, con semplici ragionamenti (cioè senza fare calcoli!) che: R(0.5)=F(0.5)=0.5; da ciò segue tra l'altro che l'affidabilità del sistema ponte è uguale a quella di ogni suo singolo componente se p=0.5; inoltre, essa risulta superiore a p se p > 0.5, inferiore se p < 0.5. Tutte le precedenti proprietà sono confermate dal grafico di R(p) in ura.

In tale grafico, assieme alla funzione R = R(p), viene riportata la curva (retta bisettrice): R₁=p, rappresentante la "funzione affidabilità" del singolo componente. Come anticipato, le due curve si intersecano solo quando p=0.5. Verifichiamolo:

Il sistema ponte è un esempio di come un sistema contenente delle "ridondanze" non sempre risulti più affidabile di ogni suo singolo componente (a meno che - ovviamente - non sia un sistema parallelo). Ciò è stato detto anche a proposito dei sistemi "SP" e PS" (si vedano anche gli esercizi proposti alla fine di questo modulo). L'eventuale miglioramento di affidabilità dipende - in generale - dai valori di affidabilità dei singoli componenti (si ricordi, a tale proposito, che l'affidabilità del sistema è in generale una funzione crescente dell'affidabilità dei componenti).

Si provi a dare una giustificazione qualitative del fatto che - nelle stesse ipotesi alla base della 3) - il sistema ponte può risultare meno affidabile del singolo componente se questo è "poco affidabile". Ciò apparirà comunque più chiaro quando si studieranno i metodi basati sugli "Insiemi di Collegamento " e "di Taglio".