| tecnica |
|
|||||
|
ESERCIZIO N° 19
Un punto materiale si muove con velocità costante lungo la circonferenza di un cerchio di raggio r=5m. esso compie un giro completo ogni 20s.
a) Quale è la velocità media del punto durante i primi 5s del suo moto ?
b) Quale è la velocità media del punto durante i primi 25s del suo moto ?
Poniamo T = 20s (periodo del moto) e t = 5s.
Allora si ha:
q(t q(0) q(t
![]()
![]() vm(t ) =
r = r
vm(t ) =
r = r
t t
Ma q(t wt dove w p/T = 0,31 rad/s
Quindi q(t
e
vm(t1) 1,57m/s
Posto ora t = 25s trattandosi di un moto circolare uniforme si ha che anche la velocità media è costante, quindi:
vm(t ) = vm(t
ESERCIZIO N° 20
Una freccia viene lanciata da un arco che le imprime una accelerazione costante per un tratto di 60cm. Se la sua velocità al momento in cui lascia l'arco è di 60m/s, che accelerazione le ha impresso l'arco ?
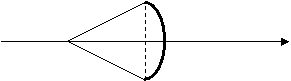
O d x
Si ponga d = 60cm = 0,6m
La velocità della freccia nel punto d è vd = 60m/s.
Il moto in esame è un moto rettilineo uniformemente vario, quindi dalla quarta equazione descrivente tale moto si ha:
vd = (vx0 + 2a(d - x con vx0 = velocità iniziale della freccia = 0
x = spostamento iniziale della freccia = (per come è stato
fissato il sistema di riferimento) = 0
Quindi vd = 2ad
da cui
vd 3600 m /s
![]()
![]() a = = m/s
a = = m/s
2d 2∙0,6m
ESERCIZIO N° 21
Un treno partito da fermo si muove con accelerazione costante. Ad un certo istante viaggia a 30m/s e 160m più avanti la sua velocità è di 50m/s. Calcolare:
a) l'accelerazione;
b) il tempo che impiega a percorrere i 160m;
c) la distanza tra il punto di partenza e quello in cui il treno ha raggiunto la velocità di 30m/s;
d) il tempo richiesto per raggiungere la velocità di 30m7s.
Sia x = posizione iniziale = 0
v = velocità iniziale = 0
t = tempo impiegato per raggiungere i 30m/s
v(t ) = velocità al tempo t = 30 m/s
x(t ) = posizione al tempo t
t = tempo impiegato per percorrere i 160m
x(t ) = x(t ) + 160m = posizione, dall'origine, dopo aver percorso i 160m
a = accelerazione
v(t ) = velocità alla posizione x(t ) = 50m/s
Per calcolare l'accelerazione occorre tenere presente che:
[v(t = [v(t + 2a(x(t ) - x(t )) = [v(t + 2a(160)
da cui
[v(t - [v(t
![]() a = 5m/s
a = 5m/s
320
Per il tempo t
x(t ) = x(t ) + ½ (v(t ) + v(t )) t
x(t ) + 160m = x(t ) + ½ (v(t ) + v(t )) t
da cui
320
![]() t = 4s
t = 4s
v(t ) + v(t
Per la x(t
[v(t = v + 2a(x(t ) - x
[v(t = 2ax(t
da cui
[v(t
![]() x(t = 90m
x(t = 90m
2a
Il tempo t si ricava da:
x(t ) = x + ½(v(t ) + v )t
da cui
2x(t
![]() t = 6s
t = 6s
v(t
ESERCIZIO N° 22
![]() Un punto
materiale A si muove lungo la linea retta y = d (=30m) con velocità costante v
(v = 3m/s) nella direzione dell'asse x positivo. Un secondo punto B parte
dall'origine con velocità iniziale nulla e con accelerazione costante a (a =
0,4m/s ) nello stesso istante in cui il punto A attraversa l'asse
y.
Un punto
materiale A si muove lungo la linea retta y = d (=30m) con velocità costante v
(v = 3m/s) nella direzione dell'asse x positivo. Un secondo punto B parte
dall'origine con velocità iniziale nulla e con accelerazione costante a (a =
0,4m/s ) nello stesso istante in cui il punto A attraversa l'asse
y.
![]()
![]() Quale
angolo dovrebbe formare a con l'asse y positivo perché si verifichi la
collisione ?
Quale
angolo dovrebbe formare a con l'asse y positivo perché si verifichi la
collisione ?
![]() y
y
![]()
![]()
![]() v
v
![]()
![]()
![]()
![]() A punto di collisione
A punto di collisione
 d = 30m q
d = 30m q
![]()
![]()
![]()
![]() a
a
![]()
![]() B x
B x
Indichiamo con t l'istante di tempo in cui avviene la collisione. In tale istante di tempo evidentemente si ha:
![]()
xA(t ) = xB(t dove xA(t ) = coordinata x del punto A al tempo t
yA(t ) = yA(t xB(t ) = coordinata x del punto B al tempo t
yA(t ) = coordinata y del punto A al tempo t
yB(t ) = coordinata y del punto B al tempo t
Si ha:
xA(t ) = vt
xB(t ) = ½(ax)(t = ½ (a∙senq)(t
yA(t ) = d
yB(t ) = ½(ay)(t = ½ (a∙cosq)(t
Dal sistema precedente si ottiene quindi:
![]()
vt = ½ (a∙senq)(t
d = ½ (a∙cosq)(t
da cui
![]() 2v
2v
![]() t
t
a∙senq
1 4v
![]()
![]() d = a∙cosq
d = a∙cosq
2 a (1- cos q)
![]() 2v cosq
2v cosq
![]() d =
d =
a(1- cos q)
2v
![]() t
t
a∙senq
Dalla prima equazione si ottiene:
adcos q + 2v cosq - ad = 0
Risolvendo:
![]() -2v 4v + 4a d -18±30 -2
-2v 4v + 4a d -18±30 -2
![]()
![]()
![]()
![]() cosq = =
cosq = =
2ad 24 0,5
Delle due soluzioni ha significato solo quella positiva, quindi:
![]() cosq q
cosq q
ESERCIZIO N° 23
Un punto si muove su traiettoria rettilinea con accelerazione costante. Quando il punto mobile transita per il punto di ascissa x la sua velocità è v , mentre quando transita per il punto di ascissa x la velocità è v . Calcolare il valore dell'accelerazione.
Trattandosi di moto rettilineo uniformemente accelerato si ha:
v(t) = v + at
x(t) = x + v t + ½ at
Dalla prima equazione ricaviamo il tempo e sostituiamo nella seconda:
v-v
![]() t =
t =
a
v 1 (v-v v - v
![]()
![]()
![]()
![]() x = x (v-v ) + a = x
x = x (v-v ) + a = x
a 2 a 2a
Con i dati del problema si ha:
v - v
![]() x = x , v = v x -x
x = x , v = v x -x
2a
v - v
![]() x = x , v = v x - x
x = x , v = v x - x
2a
Sottraendo la prima relazione dalla seconda si ha:
1 v - v
![]()
![]() x - x = (v - v - v + v
x - x = (v - v - v + v
2a 2a
da cui
v - v
![]() a =
a =
2(x - x
ESERCIZIO N° 24
In prossimità della superficie della Terra, in assenza di attriti, tutti i corpi sono sottoposti all'accelerazione di gravità g = 9,8m/s , diretta verticalmente verso il basso.
Se un copro viene lanciato verticalmente verso l'alto con velocità v , calcolare la massima quota e la velocità con cui ricade al suolo.
Nella fase di salita il moto è ritardato perché l'accelerazione di gravità e lo spostamento sono paralleli ma discordi:
![]()
v(t) = v - gt
SALITA 1
![]() y(t) = y + v t - gt
y(t) = y + v t - gt
2
Se il punto di lancio viene posto nell'origine ed il lancio è effettuato per t=0, si ha y
La massima quota ymax = h è caratterizzata dal fatto che vi si realizza un'inversione di marcia: La velocità, inizialmente diretta verso l'alto, diventa nulla, per poi iniziare la fase di discesa con direzione orientata verso il basso.
Dunque detto t il tempo necessario a raggiungere la massima quota, si ha:
![]() v(t ) = 0 =
v - gt t = v /g
v(t ) = 0 =
v - gt t = v /g
1 v 1 v v
![]()
![]()
![]()
![]()
![]() ymax = h = v t - gt = - =
ymax = h = v t - gt = - =
2 g 2 g 2g
La fase di discesa è caratterizzata da una partenza a velocità iniziale nulla (vin = 0) da una quota h, con accelerazione concorde al verso di spostamento (moto accelerato).
Detto t=0 l'istante di inizio della fase di discesa si ha:
![]()
v(t) = vin - gt = -gt
DISCESA 1 1
![]()
![]() y(t) = h + vint - gt = h
- gt
y(t) = h + vint - gt = h
- gt
2 2
L'arrivo al suolo avviene dopo un tempo t tale che y(t

1 2h
![]()
![]()
![]() y(t ) = 0 =
h - gt t
y(t ) = 0 =
h - gt t
2 g
La velocità di arrivo al suolo è:

2h
![]()
![]() v = v(t ) = -
g = - 2gh
v = v(t ) = -
g = - 2gh
g
Tenendo conto che h = v /2g si ha:
v
![]() v 2g = -v
v 2g = -v
2g
Il corpo arriva al suolo con una velocità pari, in modulo, a quella di lancio, ma con verso opposto.
ESERCIZIO N° 25
Un proiettile è sparato orizzontalmente con velocità iniziale v = 50m/s da una posizione a quota h = 100m rispetto al suolo orizzontale. In assenza di attriti, con quale inclinazione rispetto al suolo il proiettile arriva a terra ?
Si consideri la ura:
![]() y
y
![]() v
v
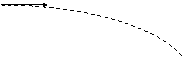
![]()
h vx
![]()
![]()
![]()
![]()
![]()
![]() q x
q x
vy
![]()
Per calcolare l'angolo q basta ricavare le componenti vx e vy della velocità nel punto di arrivo al suolo. Infatti:
tgq = vy/vx
Le equazioni delle componenti della velocità sono:
vx = v (poiché ax = 0 e quindi vx = cost)
vy = -gt (ay = -g e vy
Il tempo t impiegato ad arrivare al suolo si ricava dall'equazione per la coordinata y, tenendo conto che al tempo t è y(t
1
![]() y(t ) = h
- gt
y(t ) = h
- gt
2
Da ciò si ricava
2h
![]() t
t
g
Dunque
vx(t ) = v = 50m/s

2h
![]()
![]() vy = -
g = - 2gh = -44,3m/s
vy = -
g = - 2gh = -44,3m/s
g
![]() tgq = vy(t )/vx(t )
=0,885 q
tgq = vy(t )/vx(t )
=0,885 q
ESERCIZIO N° 26
Un punto materiale è lanciato orizzontalmente, con velocità v , dalla sommità di una torre. Ricavare l'espressione, in funzione del tempo, delle componenti tangenziale e normale dell'accelerazione.
Il moto, in assenza di attriti, avviene con accelerazione pari all'accelerazione di gravità g.
![]() y
y
![]()
![]()
 v n
v n
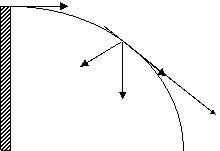
![]() an at vy q v
an at vy q v
![]()
![]()
![]()
![]() vx t
vx t
![]()
![]() g t
g t
![]()
x
![]()
![]() a = g
a = g
![]() an = gsenq
an = gsenq
at = gcosq
![]() g = an + at
g = an + at
Il calcolo dell'angolo q può essere fatto a partire dalle componenti sectiunesiane della velocità:
tgq = vy/vx
dove
![]()
vx = v
![]() tgq = - v /gt
tgq = - v /gt
vy = -gt
Nelle espressioni an = gsenq, at = gcosq, occorre ora esprimere senq e cosq in funzione di tgq
tgq
![]()
![]() senq
senq
1+ tg q
1
![]()
![]() cosq
cosq
1 + tg q
 v 1 gv
v 1 gv
![]()
![]()
![]()
![]() an = gsenq = g =
an = gsenq = g =
gt v v + g t
![]() 1 +
1 +
g t
1 g t
![]()
![]()
![]() at = gcosq = g =
at = gcosq = g =
v v + g t
![]() 1 +
1 +
g t
ESERCIZIO N° 27
Un proiettile è sparato orizzontalmente con velocità v = 30m/s. In assenza di attriti, qual è il raggio di curvatura della traiettoria dopo 2s dal lancio ?
Procedendo come nell'esercizio n.26 si ha
![]()
![]() vx = v
vx = v
![]()
![]() v = vx + vy = v + g t
v = vx + vy = v + g t
vy = -gt
ed inoltre
gv
![]() an
an
![]() v + g t
v + g t
Il raggio di curvatura è dato dalla relazione:
![]() v v (v + g t ) (v + g t
v v (v + g t ) (v + g t
![]()
![]()
![]()
![]()
![]() a R = = v + g t = = 156,5m
a R = = v + g t = = 156,5m
R an gv gv
|
Privacy
|
© ePerTutti.com : tutti i diritti riservati
:::::
Condizioni Generali - Invia - Contatta