| tecnica |
|
ESERCIZIO N° 28
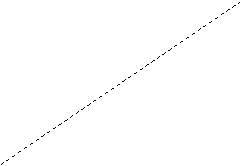
Un uomo, posto nell'origine di un sistema di riferimento, lancia una freccia puntando direttamente, nella direzione di visione, verso una scimmia S ferma su un albero. La scimmia intuisce l'intenzione aggressiva e, nell'istante in cui parte la freccia, si lascia cadere al suolo. L'ignoranza della cinematica è fatale alla scimmia, che viene centrata al volo. Perché ?
Occorre verificare che indipendentemente dalla velocità iniziale, esiste un punto in cui freccia e scimmia arrivano contemporaneamente.
![]()
![]()
![]()
![]()
![]() y S
y S
H
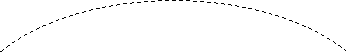 v S'
v S'

![]()
![]() q
q

![]() Q x
Q x
d
Indicando con yf(t) ed ys(t) le quote della freccia e della scimmia rispettivamente, si ha:
![]() 1
1
![]() yf(t) = (v senq)t - gt
yf(t) = (v senq)t - gt
2
1
![]() ys(t) = H
- gt
ys(t) = H
- gt
2
La scimmia viene colpita se, al tempo t in cui la freccia e scimmia hanno la stessa quota y, avviene anche che l'ascissa xf della freccia coincida con l'ascissa d (costante) della scimmia: questo significa l'arrivo simultaneo di freccia e scimmia nel punto S'. Dunque:
1 1
![]()
![]()
![]() yf(t ) = ys(t yf(t) = (v senq)t - gt = H
- gt
yf(t ) = ys(t yf(t) = (v senq)t - gt = H
- gt
2 2
da cui
![]() t
t
v senq
L'ascissa della freccia ha la legge oraria : xf(t) = (v cosq)t per cui, al tempo t , si ha:
![]()
![]() xf(t ) = v cosq =
xf(t ) = v cosq =
v senq tgq
ma H = dtgq (nel triangolo rettangolo PSQ) per cui
![]() xf(t = d = xs
xf(t = d = xs
tgq
Dunque al tempo t freccia e scimmia hanno le stesse coordinate e la scimmia è colpita.
E' da osservare che quanto sopra trovato non dipende dalla velocità della freccia (purché v sia tale che la gittata della freccia sia superiore alla distanza d).
ESERCIZIO N° 29
Le lancette di un orologio indicano le ore tre. Dopo quanto tempo le lancette si ritrovano per la prima volta ad angolo retto ?
Si tratta di due moti angolari uniformi, a diverse velocità angolari, riguardanti le due lancette (ore e minuti).
In un moto angolare uniforme l'andamento temporale del parametro cinematico angolo q è espresso dalla relazione:
q(t) = q wt
La legge appena scritta vale per entrambe le lancette (ore e minuti); nel caso della lancetta delle ore si ha:
wore p/Tore p/12h (un giro intero in 12 ore) = 0,523 rad/h
mentre per la lancetta dei minuti:
wmin p/Tmin p/1h (un giro intero in 1 ora) = 6,28 rad/h
Prendendo come raggio di riferimento per gli angoli la linea verticale (corrispondente quindi a q=0) si ha:
lancetta delle ore: qore(t) = qore0 woret dove qore0 p/2 (posizione iniziale sulle ore tre)
Quindi qore(t) = p woret
Per la lancetta dei minuti: qmin(t) = qmin0 wmint dove qmin0 (posizione iniziale verticale)
Quindi qmin(t) = wmint
Cerchiamo quindi il valore t di t, tale che qmin qore p/2; dunque
![]()
qmin(t wmint
qmin qore -p wmin - w ore)t
qore(t p woret
Pertanto
p
![]() t = 0,55h 33min =
6/11 h
t = 0,55h 33min =
6/11 h
wmin - w ore
ESERCIZIO N° 30
La piattaforma di una giostra si muove di moto circolare non uniforme. Essa parte da ferma ed ha un'accelerazione angolare costante a = 0,2 rad/s . Calcolare:
la velocità angolare dopo 2s;
l'accelerazione, in modulo, di un punto della piattaforma che disti r = 2m dall'asse di rotazione.
Dalla relazione
dw
![]() = a = cost
= a = cost
dt
si ha
![]()
w(t) = adt + cost = at + cost
dove la costante rappresenta il valore iniziale (t = 0) della velocità angolare, w
w(t) = at + w
Poiché la giostra parte da ferma si ha w = 0 e quindi:
w(t) = at
Per t = 2s si ha
w(2) = (0,2rad/s ) · (2s) = 0,4 rad/s
L'accelerazione vettoriale del punto è:
![]()
![]()
![]() dv(t) d[v(t)
t(t)] dv d t
dv(t) d[v(t)
t(t)] dv d t
![]()
![]()
![]()
![]()
![]()
![]() a = = = t + v
a = = = t + v
dt dt dt dt
Il modulo della velocità vale v = wr, con r distanza del punto dall'asse di rotazione. Dunque
![]()
dv d(wr) dw
![]()
![]()
![]() at = = = r =
ra
at = = = r =
ra
dt dt dt
v
![]() an = = w r, w at
an = = w r, w at
r
Nel problema in esame l'accelerazione tangenziale è costante nel tempo, mentre la componente normale cresce col quadrato del tempo. Il modulo dell'accelerazione ha dunque l'espressione:
![]()
![]()
![]() a = at + an a r a r t ar 1 + a t
a = at + an a r a r t ar 1 + a t
ESERCIZIO N° 31
L'equazione oraria di un punto mobile che si muove su traiettoria rettilinea è s = At - Bt.
Determinare le dimensioni fisiche delle due grandezze denominate A e B e le rispettive unità di misura;
ricavare le espressioni temporali della velocità e dell'accelerazione, deducendo il significato fisico di B;
trovare gli istanti di arresto del punto.
Poiché lo spazio percorso ha le dimensioni fisiche di una lunghezza, dalla legge oraria del moto se ne deduce che deve essere soddisfatta la seguente equazione dimensionale:
[L] = [A] [T] - [B] [T]
e cioè deve essere:
![]() [L] = [A] [T] [A] = [L] [T]
[L] = [A] [T] [A] = [L] [T]
![]() [L] = [B] [T] [B] = [L] [T]-l
[L] = [B] [T] [B] = [L] [T]-l
Le unità di misura di A e B sono dunque m s e m s-l rispettivamente.
L'espressione temporale della velocità e dell'accelerazione si ottengono per derivazione della legge oraria, cioè
ds
![]() v = =3At - B
v = =3At - B
dt
dv d s
![]()
![]() a = = = 6At
a = = = 6At
dt dt
Dalla prima se ne deduce il significato fisico di B: essa rappresenta la velocità del punto al tempo t=0 (velocità iniziale).
Per trovare gli istanti di arresto del corpo basta uguagliare v a zero e risolvere rispetto al tempo:
v = 3At - B = 0
da cui:
B
![]() t =
t =
3A
Affinché tale equazione abbia soluzioni reali deve essere
B
![]() >0 e cioè contemporaneamente A>0 e B>0 oppure contemporaneamente
A<0 e B<0.
>0 e cioè contemporaneamente A>0 e B>0 oppure contemporaneamente
A<0 e B<0.
3A
ESERCIZIO N° 32
Un punto materiale si muove di moto circolare uniforme con velocità angolare (costante) w, lungo una circonferenza di raggio r = 1.
Scrivere l'equazione oraria del moto.
![]()
![]() Scelto un sistema di assi sectiunesiani
Oxy, con origine nel centro della circonferenza, scrivere l'equazione OP(s)
della traiettoria e l'equazione OP(t) del moto.
Scelto un sistema di assi sectiunesiani
Oxy, con origine nel centro della circonferenza, scrivere l'equazione OP(s)
della traiettoria e l'equazione OP(t) del moto.
Trattandosi di un moto uniforme, l'equazione oraria è data da:
s = s + v t
dove s = arco di circonferenza percorso al tempo t
s = arco di circonferenza iniziale.
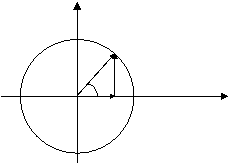
Si consideri ora la seguente ura:
 y
y
P
![]() q W x
q W x
O H
Supponiamo che al tempo t=0 il punto si trovi sovrapposto al punto W. Si ha allora:
s
e quindi
s = v t
![]()
Per ricavare l'equazione della traiettoria scomponiamo il vettore OP nella somma delle sue due componenti vettoriali lungo i due assi:
![]()
![]()
![]()
OP = OH + HP
![]()
![]() con OH = (rcosq) i
con OH = (rcosq) i
![]()
![]() HP = (rsenq) j
HP = (rsenq) j
![]()
Avendo scelto l'asse x lungo la direzione OW W origine sulla traiettoria) la lunghezza dell'arco WP è s e quindi:
s
![]() q
q
r
![]()
Da ciò si ricava l'equazione OP(s) della traiettoria:
![]() s s
s s
![]()
![]()
![]()
![]() OP(s) =
(rcos ) i + (rsen ) j
OP(s) =
(rcos ) i + (rsen ) j
r r
![]() Tenuto
conto poi che s = v t, si ricava l'equazione OP(t) del moto:
Tenuto
conto poi che s = v t, si ricava l'equazione OP(t) del moto:
![]() v t v t
v t v t
![]()
![]()
![]()
![]() OP(t) =
(rcos ) i + (rsen ) j
OP(t) =
(rcos ) i + (rsen ) j
r r
che può essere scritta (ricordato che w = v /r)
![]()
![]()
![]() OP(t) =
(rcos wt) i
+ (rsen wt) j
OP(t) =
(rcos wt) i
+ (rsen wt) j
ESERCIZIO N° 33
Il moto di un punto P è descritto dall'equazione:
![]()
![]()
![]()
![]() OP(t) =
(Acos(at)) i
+ (Asen(at)) j
+ (bt g) k
OP(t) =
(Acos(at)) i
+ (Asen(at)) j
+ (bt g) k
Determinare le dimensioni fisiche di A, a b g
Trovare il versore tangente alla traiettoria quando A=2m, a=2s-l b=3m/s, g=2m.
Determinare il raggio di curvatura della traiettoria.
Determinare l'equazione oraria s=s(t).
Studiare la forma della traiettoria, deducendone infine il passo.
![]()
Il vettore OP(t) ha le dimensioni di una lunghezza. Ne segue quindi:
[L] = [Acos(at)]
[L] = [Asen(at)]
[L] = [bt g
Dalla terza si ricava:
g] = [L]
b] = [L][T]-l
Dato che sen e cos sono funzioni, esse devono essere adimensionali, e dato che l'argomento di una funzione deve essere anch'esso adimensionale si ha:
[A] = [L]
a] = [T]-l
Per trovare il versore tangente alla traiettoria, basta osservare che il vettore velocità è sempre tangente alla traiettoria, quindi possiamo scrivere:
![]() dOP
dOP
![]()
![]() v dt
v dt
![]()
![]()
![]() t = =
t = =
![]()
![]()
![]()
![]()
![]()
![]() v v
v v
![]() Derivando
OP si ottiene:
Derivando
OP si ottiene:
![]() dOP
dOP
![]()
![]()
![]()
![]()
![]() v = = ( Aasen(at)) i + (Aacos(at)) j + b k
v = = ( Aasen(at)) i + (Aacos(at)) j + b k
dt
Quindi:
![]()
![]()
![]()
![]()
![]()
![]() v = vx + vy + vz = A a sen at) + A a cos at) + b = A a b
v = vx + vy + vz = A a sen at) + A a cos at) + b = A a b
Sostituendo i valori A=2m, a=2s-l b=3m/s, g=2m si ottiene
![]()
![]()
![]() v =
5m/s
v =
5m/s
![]()
![]()
![]() ( Aasen(at)) i + (Aacos(at)) j + b k -4sen(2t) 4cos(2t)
( Aasen(at)) i + (Aacos(at)) j + b k -4sen(2t) 4cos(2t)
![]()
![]()
![]()
![]()
![]()
![]()
![]() t =
= i + j +3k
t =
= i + j +3k
5 5 5
![]()
![]()
![]() Dal
fatto che v è indipendente dal tempo, ne segue che il
moto è uniforme. Il punto materiale sarà dunque soggetto alla sola
accelerazione centripeta:
Dal
fatto che v è indipendente dal tempo, ne segue che il
moto è uniforme. Il punto materiale sarà dunque soggetto alla sola
accelerazione centripeta:
v
![]()
![]()
![]()
![]() acp = n dove n
è il versore normale alla traiettoria
acp = n dove n
è il versore normale alla traiettoria
r
Da ciò si ricava
v
![]() acp = (essendo n = 1)
acp = (essendo n = 1)
r
Quindi
v
![]() r =
r =
acp
Occorre dunque ricavare acp. Sapendo che l'accelerazione si ottiene per derivazione della velocità, si ottiene:
![]() dv
dv
![]()
![]()
![]()
![]() a = = ( Aa cos(at)) i + ( Aa sen(at)) j
a = = ( Aa cos(at)) i + ( Aa sen(at)) j
dt
![]()
![]()
![]() a = A a cos at) + A a sen at) = A a = Aa
a = A a cos at) + A a sen at) = A a = Aa
Quindi il raggio di curvatura è
v A a b
![]()
![]() r = = = 3,125m
r = = = 3,125m
acp A a
![]() d s
d s
dt
![]()
![]() d s = vdt
d s = vdt
Da questa relazione, valutando i moduli, otteniamo:
![]() ds = vdt =
A a b dt
ds = vdt =
A a b dt
L'equazione oraria s(t) si ottiene integrando tale uguaglianza:
![]()
![]()
s t
ds
= ![]() A a b dt
A a b dt
dove abbiamo scelto come origine sulla traiettoria la posizione occupata dal punto all'istante t=0. Si ottiene quindi
![]()
s = A a b t
equazione tipica del moto uniforme.
![]()
![]() Il moto
di P può essere visto come la sovrapposizione di due movimenti, uno lungo lasse
z e l'altro in un piano parallelo al piano x-y. Il primo è un moto rettilineo
uniforme, perché vz, che è uguale a b, è costante nel tempo. Il secondo è un moto circolare
uniforme come appare confrontando la (rcos(wt)) i + (rsen(wt)) j dell'esercizio precedente, l'espressione
Il moto
di P può essere visto come la sovrapposizione di due movimenti, uno lungo lasse
z e l'altro in un piano parallelo al piano x-y. Il primo è un moto rettilineo
uniforme, perché vz, che è uguale a b, è costante nel tempo. Il secondo è un moto circolare
uniforme come appare confrontando la (rcos(wt)) i + (rsen(wt)) j dell'esercizio precedente, l'espressione
![]()
![]() (Acos(at)) i + (Asen(at)) j
(Acos(at)) i + (Asen(at)) j
che rappresenta la posizione di OP su un piano parallelo a x-y. ne segue che la traiettoria è un'elica cilindrica
Nel tempo T=2p a che occorre per compiere un'intera circonferenza (periodo del moto circolare che avviene nel piano parallelo), l'avanzamento nella direzione z è
sz bT = b p a
che rappresenta appunto il passo dell'elica.
ESERCIZIO N° 34
Un punto materiale si muove nel piano x-y con equazione data da:
![]()
![]()
![]() OP = ct i + be-kt j (con t > 0)
OP = ct i + be-kt j (con t > 0)
Trovare le dimensioni fisiche di c, b, k.
Determinare l'equazione della traiettoria.
Trovare la dipendenza temporale della velocità e dell'accelerazione. Studiare il moto nel caso asintotico tV
![]()
Poiché OP ha le dimensioni fisiche di una lunghezza, allora anche ct e be-kt devono avere tale dimensione. Ricordato che una funzione è adimensionale, si ha:
[b] = [L]
[c] = [L][T]-l
Inoltre poiché l'argomento di una funzione deve essere adimensionale anch'esso, allora:
[k] = [T]-l
Per determinare l'equazione della traiettoria, scriviamo la legge oraria nella rappresentazione sectiunesiana:
![]() x(t) = ct
x(t) = ct
y(t) = be-kt
Ricavando t dalla prima e sostituendo nella seconda si ottiene l'equazione della traiettoria:
x
![]() t =
t =
c
y(x) = be-kx/c
![]()
![]() dOP dv
dOP dv
dt dt
![]()
dx(t)
![]() vx = = c
vx = = c
![]()
![]() dt
dt
da cui v = vx + vy = c + k b e-2kt
dy(t)
![]() vy = = b(-k)e-kt
vy = = b(-k)e-kt
dt
![]() dvx
dvx
![]() ax = = 0
ax = = 0
![]()
![]() dt
dt
da cui a = ax + ay = ay = ay
dvy
![]() ay = = bk e-kt
ay = = bk e-kt
dt
xV
yV
![]()
![]() vV c = c
vV c = c
aV
Il moto tende a diventare uniforme e la traiettoria tende asintoticamente all'asse x.
ESERCIZIO N° 35
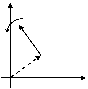
![]() Nel
piano x-y un versore u ruota con
velocità angolare costate mantenendo la sua origine fissa nell'origine O del
sistema di assi.
Nel
piano x-y un versore u ruota con
velocità angolare costate mantenendo la sua origine fissa nell'origine O del
sistema di assi.
![]() Calcolare
du/dt.
Calcolare
du/dt.
![]()
![]()
![]()
![]() Indicato
con t il versore normale ad u
ed orientato nel verso in cui si muove l'estremo libero di u, calcolare dt /dt.
Indicato
con t il versore normale ad u
ed orientato nel verso in cui si muove l'estremo libero di u, calcolare dt /dt.
![]()
![]()
![]() y y
y y
![]()
![]() t
t
![]() u
u
x x
![]()
![]()
![]()
![]()
![]() L'estremo
libero di u percorre una traiettoria
circolare di raggio 1. Il suo moto è allora un moto circolare uniforme (in
quanto w=cost). Ricordato che il vettore
velocità è sempre tangente alla traiettoria e diretto come il verso di
percorrenza lungo la traiettoria, e ricordato che dato un vettore a di modulo
costante, il quale ad un certo istante ruoti con velocità angolare pari ad w, la sua derivata da/dt è un vettore di modulo pari ad wa e ruotato rispetto ad a di p/2 nel senso in cui ruota a, si ha:
L'estremo
libero di u percorre una traiettoria
circolare di raggio 1. Il suo moto è allora un moto circolare uniforme (in
quanto w=cost). Ricordato che il vettore
velocità è sempre tangente alla traiettoria e diretto come il verso di
percorrenza lungo la traiettoria, e ricordato che dato un vettore a di modulo
costante, il quale ad un certo istante ruoti con velocità angolare pari ad w, la sua derivata da/dt è un vettore di modulo pari ad wa e ruotato rispetto ad a di p/2 nel senso in cui ruota a, si ha:
![]() du
du
![]()
![]() v =
v =
dt
In modulo:
![]()
![]()
![]() du
du
![]() v = = w
v = = w
dt
![]()
![]() Indicato
con t un versore tangente alla traiettoria nel punto P (estremo
libero di u) ed orientato nel verso
del moto si ha:
Indicato
con t un versore tangente alla traiettoria nel punto P (estremo
libero di u) ed orientato nel verso
del moto si ha:
![]()
![]()
![]() v = vt wt
v = vt wt
Quindi
![]() du
du
![]()
![]() wt
wt
dt
![]()
![]()
![]() Il
versore t, essendo costantemente perpendicolare ad u, ruota anch'esso con velocità angolare
w. Applicando le stesse considerazioni
fatte per du/dt si ottiene:
Il
versore t, essendo costantemente perpendicolare ad u, ruota anch'esso con velocità angolare
w. Applicando le stesse considerazioni
fatte per du/dt si ottiene:
![]() dt
dt
![]()
![]() = -wu
= -wu
dt
![]()
![]()
![]()
![]() Infatti
la derivata di t deve avere modulo pari ad w e deve essere diretto perpendicolarmente a t, cioè
come u ed avere verso opposto a
quello di u.
Infatti
la derivata di t deve avere modulo pari ad w e deve essere diretto perpendicolarmente a t, cioè
come u ed avere verso opposto a
quello di u.
|
Privacy
|
© ePerTutti.com : tutti i diritti riservati
:::::
Condizioni Generali - Invia - Contatta