Esercitazione dodicesima - Insert sort (XII)

Esercitazione dodicesima

Questa esercitazione è presentata in due parti:

nella prima parte viene presentata la codifica in Pascal di un programma che ordini un array di interi mediante tecnica dell' "insert sort".

Nella seconda parte viene presentato il flowchart di tale programma e ne viene studiata la relativa correttezza.
Insert sort (XII)

program insert_sort ;

uses crt ;

type vet  = array [ 0..9 ] of integer ;

var  v : vet ;

var i,n :integer ;

procedure insert ( var v : vet ) ;

var j, i, temp : integer ;

begin

i := 2 ;

while i < = 9 do  begin

temp := v [ i ] ;

j := j - 1

while v [ i ] < v [ j ] do begin

v [ j+1 ] := v [ j ] ;

j := j - 1 ;

end ;

v [ j+1 ] := x ;

i := i + 1

end;

end ;

begin

clrscr ;

v [ 0 ] := 0 ;

for i := 1 to 9 do begin

writeln ( 'Inserisci il ', i, ' numero : ' ) ;

readln ( n ) ;

v [ i ] := n ;

end ;

insert ( v );

for i := 0 to 9 do write ( v [ i ] );

readln ;

end .

Flowchart relativo alla procedura insert

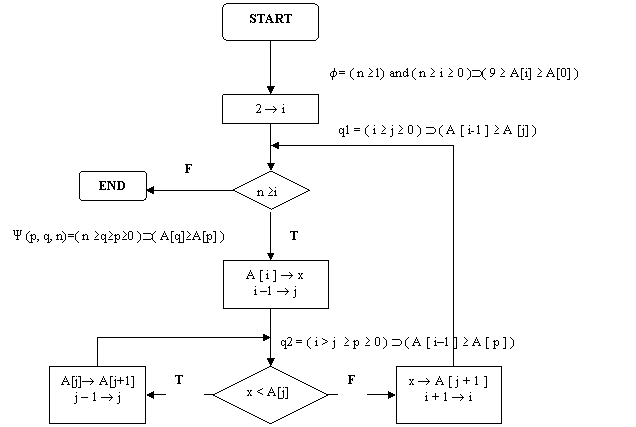
Dimostrazione di correttezza del flowchart

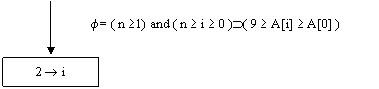
			q1 = ( 2 > j ( A [ 1 ] A [j] )

( ( n 1) and ( n i A[i] A[0] ) ) ( 2 > j ( A [ 1 ] A [ j ] )

Poiché la seconda parte è sempre vera ( potendo j essere o 0 o 1 A [ 1 ] = A [ 1 ] sempre, oppure A [ 1 ] sempre > A [ 0 ] = 0 ) l'implicazione è sempre vera

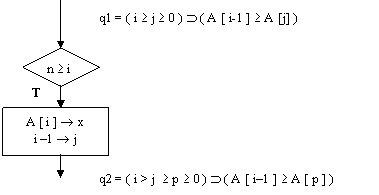
( ( i j ( A [ i-l ] A [j] ) and n i ) ( p = 0 ) ( A [ 1 ] A [ 0 ] ) )

l'implicazione è sempre vera in quanto A [ 0 ] è sempre minore del resto dell'array

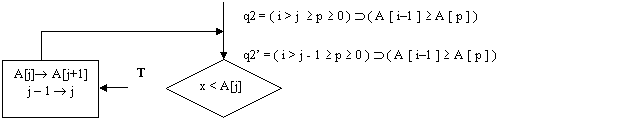
( ( i > j  p ( A [ i-1 ] A [ p ] ) and x < A [ j ] ) (( i > j - 1 p ( A [ i-1 ] A [ p ] ) )

poiché per ipotesi A [ i -l ] A [ p ] per j  p 0 lo sarà anche per j - 1 p 0 quindi l'implicazione è vera

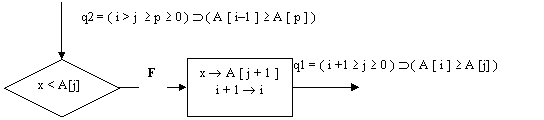
( ( i > j  p ( A [ i-1 ] A [ p ] ) and x A [ j ] ) ( ( i+1 j ( A [ i ] A [ j ] ) )

se i > j 0 ovviamente sarà anche i + 1 j 0 e, essendo x = A [ i ] ovviamente A [ i] A [ j ]

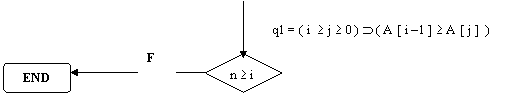
	Y (p, q, n)=( n q p ( A[ q ] A [ p ]  )

( ( i  j ( A [ i -1 ] A [ j ]  ) and i > n ) ( ( n q p ( A[ q ] A [ p ]  ) )

se q = i -1 e p = j si ha che se ( A [ i -1 ] A [ j ]  ) ovviamente sarà ( A[ q ] A [ p ]  )

quindi il flowchart è corretto .