L'AMPIEZZA DI PROBABILITA' E L'EQUAZIONE DI SCHRÖDINGER - l'equazione di diffusione per l'evoluzione all'indietro

L'AMPIEZZA DI PROBABILITA' E L'EQUAZIONE DI SCHRÖDINGER

Per spiegare l'esperimento di diffrazione di particelle si introduce un modello in cui lo stato di una particella è definito da una funzione complessa y(x,t) detta ampiezza di probabilità o funzione d'onda che gode delle seguenti proprietà:

Il modulo quadro dell'ampiezza di probabilità è la densità di probabilità con cui si osserva la particella nell'intorno del punto x al tempo t.

Alle ampiezze di probabilità si applicano le leggi classiche di composizione della probabilità.

Si aggiungono poi dei fattori moltiplicativi per normalizzare le y

Queste proprietà sono sufficienti a spiegare il fenomeno della diffrazione delle particelle. Si ragiona in questo modo: se associamo l'ampiezza di probabilità y (x,t) allo stato della particella che si determina quando una delle due fenditure è ostruita[1] e y (x,t) allo stato della particella che si determina quando l'altra fenditura è ostruita, lo stato corrispondente ad ambedue le fenditure aperte si ottiene dalla combinazione con egual peso di y (x,t) e y (x,t) (e qui abbiamo applicato una legge classica di composizione delle probabilità):

y(x,t) = a y (x,t)+y (x,t)]

Il coefficiente a (in generale complesso e funzione del tempo) si determina dalla condizione di normalizzazione (il modulo quadro della y deve essere una densità di probabilità):

y (x,t)y(x,t) = 1

Che solo y (x,t e y (x,t) intervengano nella espressione dello stato è conseguenza del fatto che se si osserva da che parte è passata la particella, possiamo ottenere solo uno tra due possibili stati, corrispondenti a y x,t o y (x,t).

che cos'e' una particella in meccanica quantistica?

Vogliamo chiarire il concetto di "probabilità di trovare la particella".

La particella in realtà non si trova in nessun posto, ma è solo il nostro senso comune che ci fa pensare ad essa come ad un punto materiale che occupa una determinata posizione nello spazio, mentre in realtà gli esperimenti ci dimostrano che ha ben altra natura. Come possiamo allora descrivere in qualche modo la particella quantistica?

In generale, nella costruzione di un modello teorico che interpreta un certo complesso fenomenologico e cerca di fare delle previsioni su di esso, il legame tra le grandezze matematiche del modello e il complesso fenomenologico si attua attraverso la definizione di alcune grandezze misurabili sperimentalmente che caratterizzano il fenomeno, che nel nostro caso è la particella.

Quindi ciascuna di queste grandezze associate alla particella sarà caratterizzata dalla sua cosiddetta "definizione operativa" ovvero dal processo fisico di misura mediante il quale la si ottiene. Questo processo può essere al limite anche un processo ideale, ottenuto come limite concettuale di un processo fisico.

Ad esempio, la grandezza "posizione" di una particella è definita mediante un processo di misura che consiste nell'investirla con radiazione di una certa lunghezza d'onda oppure porre un corpo assorbente sul suo cammino (anche se non è esatto parlare di cammino).

Questo processo fornisce una terna di valori di coordinate e ciò ci porta ad immaginare la particella presente in un certo punto dello spazio.

Quindi quando si parla di probabilità di trovare la particella in un punto si intende la probabilità che effettuando la misura della "posizione" si ottengano proprio i valori di coordinate di quel punto.

Infatti in realtà vedremo che la meccanica quantistica descrive la particella come una sovrapposizione di tante situazioni diverse. E' come se in ogni istante essa fosse presente contemporaneamente in più punti; in alcuni più presente ed in altri di meno.

Quando andiamo a misurare la sua posizione, essa si addensa istantaneamente in un punto (si dice che la particella "salta" in un autostato della posizione). Oppure potremmo vedere l'operazione di misura come una specie di filtro, che seleziona solo un valore di posizione.

modelli di evoluzione probabilistica nel tempo: diffusione classica

Ci proponiamo di determinare la legge di evoluzione temporale della y(x,t) in generale. Come preliminare determiniamo una legge di evoluzione della densità di probabilità nota come legge di diffusione

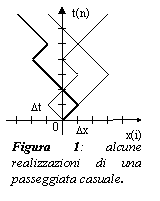
Consideriamo come primo esempio una "passeggiata casuale" in cui un punto mobile si trova nell'origine al tempo iniziale e compie un spostamento verso destra o verso sinistra di ampiezza Dx nell'intervallo di tempo Dt con uguale probabilità ½. La registrazione della posizione del punto in corrispondenza degli istanti di tempo selezionati rappresenta una traiettoria o realizzazione del processo stocastico. L'insieme delle traiettorie è detto ensemble delle realizzazioni.

Possiamo calcolare la probabilità P(i,n) di trovare la particella nel punto i Dx all'istante n Dt osservando che: se n_s e n_d sono il numero di volte che la particella si sposta a sinistra e a destra per raggiungere iDx, si avrà:

Ricaviamo che n_d=i+n_s=i+n­ n_d quindi n_d=(i+n)/2.

Ora, la probabilità di trovare la particella in i, corrisponde alla probabilità che essa compia n_d=(i+n)/2 passi a destra e quindi vale:

   con p=1/2

Quindi in definitiva si ottiene:

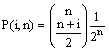
Osserviamo che la probabilità P(i,n+1) è direttamente legata alle probabilità P(i 1,n) e P(i+1,n): infatti la particella si può trovare in iDx al tempo (n+1)Dt solo se al tempo nDt si trovava in (i Dx o in (i+1)Dx, quindi:

P(i,n+1) = P(passo a destra  a nDt era in i-l) + P(passo a sinistra a nDt era in i+1

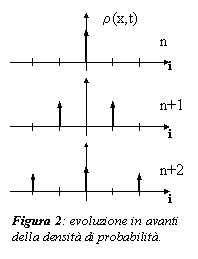
E' facile rendersi conto che con tale legge di evoluzione, la probabilità di osservare la particella lontano dall'origine cresce nel tempo; basta osservare l'evoluzione della densità di probabilità.

In ura 2 ad es. è riportata l'evoluzione nel caso che al tempo nDt la particella si trovi nell'origine (quindi la densità di probabilità r(x,nDt) è un impulso nell'origine).

La formula appena trovata definisce l'evoluzione "in avanti" nel tempo, dove per "in avanti" si intende che la densità di probabilità al tempo (n+1)Dt è espressa in funzione della densità al tempo precedente nDt.

Se invece proviamo a ricavare l'evoluzione "all'indietro" nel tempo[2], otteniamo l'equazione alternativa (la particella si poteva trovare in i al tempo n se al tempo n la osservo o in i o in i+1):

P(i,n-l) =

I fattori ½, che si riferivano precedentemente alle probabilità di abbandonare una certa posizione compiendo un passo a destra o a sinistra, si associano ora alle probabilità di pervenire ad una certa posizione compiendo un passo a destra o a sinistra.

E'importante evidenziare l'irreversibilità della diffusione classica, che si vede nel fatto che se invertiamo il tempo non possiamo più usare la stessa equazione . Inoltre osserviamo che la conurazione P(i,n-l) che si ottiene dalla nota conurazione P(i,n) nell'evoluzione all'indietro è la stessa conurazione P(i,n+1) che si ha nell'evoluzione in avanti sempre a partire da P(i,n). Invertendo il tempo non si possono ripercorrere le stesse conurazioni, come avviene invece per i fenomeni reversibili.

Vogliamo ora introdurre il limite in cui sia l'ampiezza del passo che l'intervallo temporale tendono a zero.

Dal teorema di De Moivre-Laplace sappiamo che se npq>>1 e k np è dell'ordine di , vale l'approssimazione:

Nel nostro caso per n>>1 T npq=n/4>>1,  k np= e , quindi, per valori di i dell'ordine di si avrà:

Posto allora t=nDt e x=iDx si avrà:

Se Dx va a 0 come , ovvero dx²=adt, otteniamo: [4]

.

La probabilità sarà allora descritta da una densità r(x,t) = 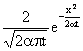, per la quale varranno le equazioni di evoluzione in avanti e all'indietro:

r(x,t+dt) = r(x dx,t) + r(x+dx,t) (

Sviluppiamo le r(x,t dx) secondo Taylor, portando lo sviluppo fino al secondo ordine:

r(x±dx,t) = r(x,t)±r_x(x,t)dx + r_xx(x,t)dx² ± .    

Sostituendo nella (1) otteniamo:

r(x,t+dt) r(x,t) =

Dividendo per dt, e tenendo conto che dx²/dt=a=D (a è interpretato come un coefficiente di diffusione), si ottiene l'equazione di diffusione per la densità di probabilità

r_t(x,t) = (

Partendo invece dall'equazione di evoluzione della densità di probabilità "all'indietro" nel tempo:

r(x,t) = r(x dx,t+dt) + r(x+dx,t+dt) 

ripetendo le considerazioni fatte per l'evoluzione in avanti otteniamo f:

r_t(x,t) =

Dalla equazione di diffusione possiamo ricavare delle condizioni sull'andamento nel tempo dei momenti m_n(t)= xⁿr(x,t)dx ovvero delle loro derivate, portando ad agire la derivata all'interno dell'integrale. Si ottiene, con un procedimento di integrazione per parti e tenendo conto delle condizioni di normalizzazione:

per n=0 e 1

per n (

Il doppio segno si riferisce all'evoluzione in avanti (+) o all'indietro (

Si noti come il momento di ordine zero altro non è che l'integrale di normalizzazione, che è ovviamente costante. Il momento di ordine uno, costante nel tempo, esprime il fatto che nel moto di diffusione la particella si muove con eguale probabilità verso destra e verso sinistra e quindi la posizione media rimane al centro. Il momento d'ordine due esprime, nel caso di primo momento nullo, l'incertezza sulla posizione del punto. Integrando nel tempo la (3) si ottiene rispettivamente per l'evoluzione in avanti o all'indietro:

m₂(t) = m₂(0) + Dt

m₂(t) = m₂(T) + D(T t)

Si noti che la costante di integrazione è stata determinata in termini dell'incertezza all'istante iniziale per l'evoluzione in avanti ed in termini dell'incertezza ad un tempo finale T per l'evoluzione all'indietro. Come già visto prima, l'irreversibità si manifesta chiaramente quando si rileva che non è possibile scegliere le costanti in modo da far coincidere a tempi intermedi le incertezze associate ai due tipi di evoluzione; infatti sia andando avanti che indietro nel tempo, l'incertezza aumenta sempre.

Una soluzione particolarmente semplice dell'equazione di diffusione si esprime come una gaussiana con varianza che evolve nel tempo con la legge del momento del secondo ordine:

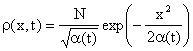con a(t) = a + Dt

Questa soluzione è ovviamente compatibile con una densità di probabilità iniziale gaussiana:

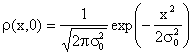(a = e N=1/

E' facile vedere che in tal caso il valor medio della posizione coincide con il valore più probabile x=0 e l'incertezza conicide con . L'evoluzione in avanti mantiene la forma gaussiana con un'incertezza che aumenta nel tempo con la legge del momento del secondo ordine:

s (t) = + Dt

Analogamente per l'evoluzione all'indietro, se al tempo finale T abbiamo:

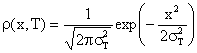
per tempi t minori di T si ottiene:

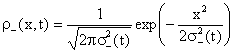con

evoluzione nel tempo dell'ampiezza di probabilità: eq.di schrödinger

Per ottenere la legge di evoluzione dell'ampiezza di probabilità è naturale tentare una generalizzazione delle equazioni di diffusione cioè ritenerle valide anche per la y

in avanti e all'indietro (

Ciò sarebbe coerente con la regola euristica di applicare le leggi valide per la probabilità alle ampiezze di probabilità. Tuttavia l'irreversibilità costituisce una difficoltà. Ci si aspetta infatti che la meccanica classica dia previsioni equivalenti a quelle della meccanica quantistica almeno nell'ambito dei fenomeni macroscopici e pertanto una proprietà qualitativa quale quella della reversibilità temporale delle equazioni di evoluzione delle grandezze osservabili deve valere, come in meccanica classica, anche in meccanica quantistica.

La grandezza osservabile è peraltro la densità di probabilità r(x,t) = y (x,t)y(x,t). Una equazione reversibile per questa grandezza deve essere tale che con le stesse condizioni al contorno per le equazioni in avanti e all'indietro, le due soluzioni sono tali che r (x,t)=r (x,t). Ciò comporta che l'equazione di evoluzione per la densità di probabilità sia una sola.

Supponiamo ad esempio che le condizioni al contorno siano che all'istante 0 le densità passino per lo stesso valore, cioè r (x,0)=r (x,0). La condizione di reversibilità si tradurrà per le y come:

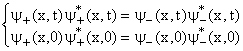
Per verificare queste uguaglianze potremmo imporre y (x,t)=y (x,t), ma ciò non sarebbe compatibile con le (4). Una condizione efficace è invece:

y (x,t)=y (x,t)   (

per imporre questa condizione dobbiamo però rendere il coefficiente di diffusione puramente immaginario, cioè sostituire D con iD:

e

In questo modo infatti, coniugando ambo i membri di ciascuna equazione, si passa dall'una all'altra e quindi la (5) è verificata.

Il confronto con una serie di proprietà sperimentali porta ad identificare il coefficiente di diffusione in termini della costante di ck e della massa della particella ottenendo cosi l'equazione di diffusione nella forma finale nota come equazione di Schrödinger per la particella libera

con

o, come viene scritta più spesso:

Più in generale, in presenza di un potenziale U(x), si giunge all'equazione:

    (

Osserviamo che se y è soluzione, y non può esserlo a meno che y=costante perché:

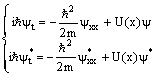
Coniugando ambo i membri della prima equazione si ottiene che[5]:

  T y_t y_t

equazione di continuità

L'ampiezza di probabilità è una grandeza complessa ed è pertanto sempre possibile esprimerla in termini di due funzioni reali associate rispettivamente al modulo ed alla fase:

y(x,t) = A(x,t) exp=     (

Il modulo A(x,t) è la radice quadrata della densità di probabilità

Per interpretare la fase S(x,t) conviene ricavare dalla equazione di Schrödinger una equazione di evoluzione per la densità di probabilità, mediante i seguenti passaggi:

r_t(x,t) = y_t(x,t)y (x,t) + y(x,t)y _t(x,t) = y_xxy +y

= y y_xx y _xxy] ;

y_xxy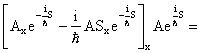

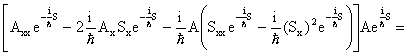
Ora, poiché:

y_xxy yy _xx = 2i Im[y_xxy ] =

Avremo:

In definitiva otteniamo la cosiddetta equazione di continuità (caso unidimensionale):

Possiamo interpretare questo risultato osservando che poiché per i fluidi si ha dove è la corrente del fluido e r la densità, possiamo pensare allora che lo stato quantistico di una particella sia assimilabile ad un modello di fluido caratterizzato da una densità di particelle (intesa come numero di particelle nell'intorno del punto diviso il numero di particelle totali) pari alla densità di probabilità e una corrente pari a rS_x/m, quindi caratterizzato da un campo di velocità S_x/m proporzionale al gradiente della fase.

Questa interpretazione la ritroveremo anche quando ci occuperemo della quantità di moto.

Si noti la differenza qualitativa con l'equazione di diffusione della densità di probabilità classica in cui l'evoluzione è determinata dalla sola densità di probabilità ai tempi precedenti.

evoluzione della fase

Analogamente si può determinare l'evoluzione della fase. Sostituendo la (7) nell'equazione di Schrödinger ( ricaviamo:

Uguagliando le parti reali ed eliminando il fattore di fase:

da cui è immediato ricavare l'equazione desiderata:

(

Nell'evoluzione della fase distinguiamo una parte "classica" associata al campo di velocità agli istanti precedenti e una parte quantistica associata alla variazione nello spazio dell'ampiezza A(x,t).