METODI GENERALI PER IL CALCOLO DELL'AFFIDABILITÀ DEI SISTEMI - Il metodo degli insiemi di taglio

parallelo). Ciò è stato detto anche a proposito dei sistemi "SP" e PS" (si vedano anche gli esercizi proposti alla fine di questo modulo). L'eventuale miglioramento di affidabilità dipende - in generale - dai valori di affidabilità dei singoli componenti (si ricordi, a tale proposito, che l'affidabilità del sistema è in generale una funzione crescente dell'affidabilità dei componenti).

Si provi a dare una giustificazione qualitative del fatto che - nelle stesse ipotesi alla base della 3) - il sistema ponte può risultare meno affidabile del singolo componente se questo è "poco affidabile". Ciò apparirà comunque più chiaro quando si studieranno i metodi basati sugli "Insiemi di Collegamento " e "di Taglio".

5.8 METODI GENERALI PER IL CALCOLO DELL'AFFIDABILITÀ DEI SISTEMI

Per il calcolo dell'affidabilità di un sistema è necessario disporre di metodi che, a partire dalla struttura funzionale del sistema, e dalla probabilità degli eventi elementari, consenta di ricavare in maniera efficiente la probabilità dell'evento finale. E' chiaro che, specie per sistemi costituiti da un numero di componenti molto grande, come sono i sistemi reali, è necessario disporre di metodi implementabili su calcolatore.

Si è già considerato il metodo della probabilità totale che - per quanto semplice - è di difficile generalizzazione (e quindi non si presta ad essere "automatizzato"). Di seguito si elencano i metodi generali più adoperati, ovvero:

a)    procedimenti basati sull'algebra degli eventi;

b)   procedimenti basati sul grafo della struttura, quale quello dei tie-set, (o insiemi di collegamento), e dei cut-set (o insiemi di taglio), facilmente implementabile su calcolatori elettronici. Un procedimento di tipo "grafico", collegato a quello dei cut-set, è quello detto "albero dei guasti" (fault-tree), qui non considerato;

c)    procedimenti basati sui processi aleatori, in particolare i processi di rinnovo e i processi di Markov (qui non trattati);

d)   procedimenti (di stima) basati sulla simulazione al calcolatore (metodo Montecarlo).

In generale i procedimenti descritti ai punti a) e b) sono utilizzati per calcolare l'affidabilità di sistemi non riparabili (o sostituibili). Quelli del punto c) - più generali e matematicamente più complessi - sono utilizzati per componenti suscettibili di riparazioni o sostituzioni, o comunque con più stati di funzionamento (componenti non binari), o per componenti statisticamente dipendenti (con o senza riparabilità). I procedimenti di simulazione, infine, consentono di analizzare sistemi per i quali la soluzione analitica sia impossibile o poco agevole.

5.8.1 Metodo dello "Spazio degli Eventi"

E' il metodo più "meccanico", basato sull'algebra degli eventi, ovvero sulla enumerazione di tutti i possibili stati di funzionamento (o di guasto) del sistema. Dato un generico sistema s, il metodo si basa essenzialmente su tre punti:

Individuazione di tutti i possibili eventi per il sistema da un punto di vista affidabilistico, cosa che corrisponde all'individuazione di tutte le possibili situazioni di funzionamento o di guasto di tutti i componenti che lo costituiscono. Tutti gli eventi enumerati sono incompatibili ed esaustivi. L'esaustività è ovvia; l'incompatibilità discende dal fatto che, data una qualsiasi coppia di eventi E_j e E_k, esiste almeno un componente che appare funzionante in E_j e guasto in E_k (v. esempio seguente);

Individuazione di tutti gli eventi che corrispondono al funzionamento del sistema;

Infine, l'affidabilità della struttura complessiva viene calcolata come la somma delle probabilità dei singoli eventi del punto 2., cosa che è possibile la incompatibilità ed esaustività.

Esempio 1. Si consideri un sistema costituito da due componenti c₁ e c₂ in parallelo; gli eventi possibili per il sistema sono:

Evento 1: C₁ e C₂; Evento 2: e C₂; Evento 3: C₁ e ; Evento 4: e .

E' semplice vedere che l'affidabilità del sistema è data dalla somma delle probabilità dei primi tre eventi:

P(S) = P(C₁ C₂) + P( C₂ ) + P(C₁ ) = 1 - P( ), come noto

Esempio 2. Si voglia calcolare l'affidabilità del sistema in ura:

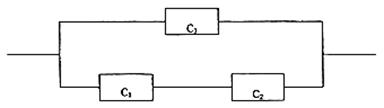I possibili eventi per il sistema sono:

Evento 1: C₁ e C₂  e C₃

Evento 2: e C₂ e C₃

Evento 3: C₁ e e C₃

Evento 4: C₁ e C₂ e

Evento 5: e e C₃

Evento 6: e C₂ e

Evento 7: C₁ e e

Evento 8: e e

Di questi, gli eventi 1, 2, 3, 4, 5 corrispondono a stati di funzionamento e l'affidabilità del sistema è data dalla somma delle loro probabilità:

P(S) = P(C₁ C₂   C₃) + P( C₂ C₃) + P(C₁ C₃) + P(C₁ C₂ ) + P( C₃).

Dagli esempi visti, è evidente che lo svantaggio principale del metodo consiste nell'enumerazione di tutti i possibili eventi, che risultano essere in numero di 2ⁿ, se n sono i componenti del sistema. Per contro, il fatto che essi siano incompatibili e esaustivi, comporta la possibilità di scrivere l'affidabilità del sistema direttamente come somma delle probabilità dei singoli eventi che ne caratterizzano il funzionamento. Questo è l'unico vantaggio rispetto ai metodi - più adoperati - dei tie-sets o dei cut-sets, esaminati nei prossimi paragrafi. Si osservi che il metodo visto consente di giungere abbastanza agevolmente al risultato finale solo nel caso di sistemi con guasti e/o riparazioni indipendenti. In caso contrario, lo sviluppo delle formule diviene di notevole complessità.

5.8.2 Il metodo degli insiemi di collegamento (tie-set)

Tale metodo si basa sulla determinazione degli insiemi minimali di collegamento (minimal tie-set), formati cioè da componenti che - se tutti funzionanti - assicurano appunto il collegamento tra ingresso e uscita nello schema di affidabilità di un sistema s (e dunque il funzionamento di s). Si consideri - ad esempio - un sistema di tre componenti (a,b,c), formato dalla serie di a con il parallelo di b e c. Gli insiemi di collegamento (tie-set) sono: t₁=(a,b); t₂=(a,c); t₃=(a,b,c); t₃ non è "minimale" in quanto contiene (a,b) e (a,c), che sono già tie-set minimali; t₁ e t₂ sono invece minimali, perché nessun loro sottoinsieme è un tie-set. E' facile rendersi conto che l'affidabilità del sistema è data dalla probabilità dell'unione degli eventi T₁ e T₂, ciascuno formato dalla serie dei componenti presenti in t₁ e in t₂ rispettivamente (si ricordi la convenzione di indicare con lettere minuscole componenti e sistemi, con le maiuscole i relativi eventi di buon funzionamento).

R = P(T₁ T₂), con T₁ = A B, T₂ = A C.

Si noti che - anche se a,b,c sono indipendenti, T₁ e T₂ non lo sono perché hanno un elemento, a, in comune. Per calcolare R mediante la precedente relazione bisogna applicare la relazione generale sulla probabilità dell'unione. Più semplicemente, si può notare, ricorrendo all'algebra degli eventi, che:

T₁ T₂ = (A B) (A C) = A (B C) , per la proprietà distributiva di unione e intersezione.

Si ritrova così la rappresentazione elementare del sistema, e quindi il risultato (in questo caso evidente): R = R_a(R_b + R_c - R_bR_c). Naturalmente, questo metodo è utile per sistemi complessi, e non certo per quello qui considerato a titolo didattico. Di seguito si illustrano le definizioni e le metodologie di calcolo generali.

Definizione. Dato un sistema s di n componenti, un sottoinsieme di suoi componenti è detto "tie-set" (TS) se è formato  da componenti che - se tutti funzionanti - assicurano il funzionamento di s. Un tie-set (indicato con la lettera minuscola t) è detto "minimale" (minimal tie-set, MTS) se non contiene sottoinsiemi che siano a loro volta dei TS. I TS vengono classificati come di ordine 1, 2, 3, , n a seconda che contengano rispettivamente 1, 2, 3, , n elementi.

Chiaramente, s è un TS di ordine n, ma in genere non è minimale (a meno che non sia un sistema serie). Determinati gli MTS (t₁,,t_n) del sistema, si indichi con T_j l'evento costituito dalla serie dei componenti di t_j. Si può dimostrare (è d'altronde intuitivo) che l'affidabilità di s è data dalla probabilità dell'unione degli eventi T_j:

R =   (1)

E' possibile, allora, rappresentare il sistema S come il parallelo degli eventi T_j, che, a loro volta, sono costituiti dalla serie degli eventi rappresentanti il funzionamento dei componenti C_j,k che lo costituiscono (). Dunque, mediante il metodo dei "tie-set", s viene rappresentato come un sistema "parallelo di serie" . Ad esempio - come già detto - un sistema serie ammette un unico tie-set, il sistema stesso (per cui la 1) diviene una identità). Un sistema parallelo invece ammette n tie-set minimali, ognuno formato da un componente, per cui la 1) restituisce la nota relazione del caso parallelo. Questi esempi verificano la validità della 1). Nel caso generale, ossia per sistemi complessi, non riducibili a sistemi serie-parallelo (p.e. il sistema ponte), il sistema "parallelo di serie" che si ottiene non è riducibile in quanto (come visto nell'esempio iniziale) gli MTS contengono degli elementi in comune: dunque, in generale, alcuni componenti appaiono "replicati" nella conurazione strutturale del sistema.

Quindi, gli eventi T_j della 1) non sono, in generale, indipendenti, poiché ogni singolo componente può ire in più di un tie-set, per cui è necessari sviluppare la (1) secondo la formula generale:

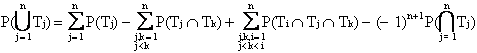(2)

La valutazione pratica nel caso di sistemi con molti componenti richiede un laborioso sviluppo di formule di probabilità. Sono possibili alcune approssimazioni; infatti, nel caso che P(T_j)<< 1 per j = 1, 2, , n, nella (2) si possono trascurare i termini di grado più elevato; fermandosi ai termini di secondo grado, ottenendo (ma ciò è di limitata applicabilità, se i componenti sono affidabili):

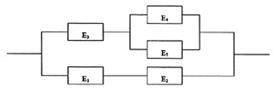Esempio: Si voglia determinare l'affidabilità del sistema in ura. I collegamenti ingresso-uscita che formano un insieme minimale sono:

T₁ = ;

T₂ = ;

T₃ = .

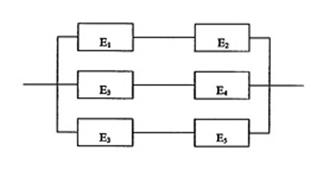
Il sistema funziona se si verifica almeno uno degli eventi T_j , quindi allo schema in ura si può sostituire uno schema formato dal parallelo dei T_j :

Il metodo dei tie-set richiede lo svolgimento di numerosi calcoli, i quali crescono vistosamente all'aumentare dei componenti del sistema e dei percorsi ingresso-uscita, sconsigliandone l'uso manuale; per contro, per la sua natura iterativa, risulta agevole costruire degli algoritmi facilmente implementabili al calcolatore. Anche se il metodo dei tie-set risulta efficiente, per la determinazione dei cammini ingresso uscita, esso non consente l'utilizzo delle formule approssimate perché nella pratica si incontrano componenti - e quindi tie-set - di affidabilità elevata; per questo motivo risulta spesso più efficiente, dal punto di vista numerico, il metodo duale degli insiemi di taglio ("cut-set").

5.8.3 Il metodo degli insiemi di taglio (cut-set)

Tale metodo si può considerare il duale di quello dei tie-set in quanto si basa sull'individuazione degli insiemi minimali di taglio (minimal cut-set) che interrompono (se formati da componenti tutti guasti) il collegamento tra ingresso e uscita.

Definizione Dato un sistema s di n componenti, un sottoinsieme di suoi componenti è detto "cut-set" (CS) se è formato  da componenti che - se tutti guasti - assicurano il guasto di s. Un cut-set (indicato con la lettera minuscola k) è detto "minimale" (minimal cut-set, MCS) se non contiene sottoinsiemi che siano a loro volta dei CS. I CS vengono classificati come di ordine 1, 2, 3, , n a seconda che contengano rispettivamente 1, 2, 3, , n elementi. Naturalmente, tutti i CS di ordine 1 sono minimali.

Si consideri ancora l'esempio del un sistema di tre componenti (a,b,c), formato dalla serie di a con il parallelo di b e c. I cut-set sono, evidentemente: k₁=(a); k₂=(b,c); k₃=(a,b,c). Si pensi ad un "taglio" che "apra" il componente a: in tal caso, s non funziona più, e così per gli altri; di tali cut-set, k₃ non è "minimale" in quanto contiene (a) e (b,c), che sono già cut-set; k₁ e k₂ sono invece minimali, perché nessun loro sottoinsieme è un cut-set. E' facile vedere l'inaffidabilità del sistema è data dalla probabilità dell'unione degli eventi corrispondenti ai guasti di k₁ e k₂, ciascuno formato dal parallelo dei propri componenti (perché un cut-set è guasto se tutti i suoi componenti sono guasti). Ciò è equivalente a rappresentare s come serie di a con il parallelo di b e c: in tal caso, quindi, la rappresentazione con i cut-set coincide anche formalmente - a differenza di quella dei tie-sets - con la rappresentazione serie-parallelo elementare. Esponiamo dunque il procedimento generale.

Determinati i MCS (k₁,..k_n), e detto l'evento "guasto di k_i", ovvero l'evento corrispondente al parallelo dei componenti presenti in k_i (k_i è guasto se si guastano tutti i suoi componenti), si può dimostrare - in maniera duale a quanto visto per il metodo dei TS che l'inaffidabilità del sistema è uguale alla probabilità che almeno un MCS sia guasto, ovvero:

F_S =   (1)

dove (2) rappresenta il non funzionamento di tutti i componenti che costituiscono il taglio k_i. Ciò corrisponde a caratterizzare K_i come sottosistema di tipo parallelo (si guasta solo se si guastano tutti i suoi componenti).

Applicando il teorema di De Morgan alla (1) si ottiene: = da cui,

(3)

Applicando ancora il teorema di De Morgan alla (2) si ottiene:

(4)

Dalla (3) si evince che è possibile rappresentare il sistema s come la serie dei sottosistemi corrispondenti agli eventi K_i, che, a loro volta, sono costituiti dal parallelo degli eventi rappresentanti il funzionamento dei componenti C_j,k che lo costituiscono, per la (4).

In definitiva, il metodo dei CS porta a rappresentare il sistema come un sistema "serie di parallelo", in maniera perfettamente duale a quella del metodo dei TS. Naturalmente, i due metodi sono perfettamente equivalenti (anche se non sempre - come visto nell'esempio precedente - danno luogo alla stessa rappresentazione, almeno apparentemente). Ad esempio, per un sistema serie tutti i componenti sono degli MCS, mentre un sistema parallelo coincide con il proprio unico MCS, e in questi casi è facile verificare la validità delle precedenti relazioni, così come anche l'equivalenza con il metodo dei TS.

Esempio: Si voglia determinare l'affidabilità del sistema in ura. Gli insiemi minimali di taglio sono:

;

;

;

;

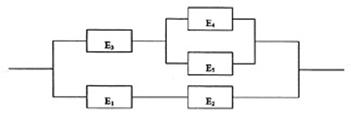
Particolarizzando la (3) si ottiene:

(3)

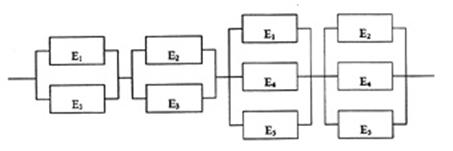
cioè, il sistema funziona se si verificano tutti gli eventi K_i , quindi si può costruire il seguente schema di affidabilità equivalente:

Lo sviluppo della (1) è alquanto laborioso, per l'eventuale presenza di tagli che potrebbero avere dei componenti in comune, rendendo gli eventi dipendenti fra loro:

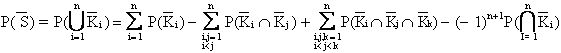(2)

In questo caso, essendo le affidabilità dei componenti prossime ad 1 (e quindi le inaffidabilità molto prossime a 0), sono possibili semplificazioni nello sviluppo della (1), nel senso di poter trascurare i termini di ordine superiore, senza commettere errori rilevanti.

Un possibile criterio di troncamento è quello che si ricava notando che sussistono le note relazioni:

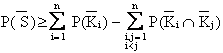= F^'

= F^''

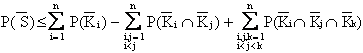= F^'''

e così via; tali disuguaglianze consentono di definire una fascia di valori, entro cui risulta compresa , utile per stabilire il livello di troncamento delle formule.

Ad esempio, fermandosi ai primi due termini risulta:

F^''_S F^'_S

L'approssimazione sarà, inoltre, tanto migliore, a parità di termini calcolati, quanto più è elevata l'affidabilità dei singoli componenti costituenti il sistema.

Si noti che in generale l'approssimazione al primo termine non può essere giustificata sulla base della "formula degli eventi rari", perché gli eventi che in essa compaiono non sono necessariamente indipendenti. In questo caso, va comunque fatto il confronto con l'approssimazione al secondo ordine. Se la differenza, DF = F'-F'', tra le due approssimazioni è inferiore al livello di precisione e desiderato, si può utilizzare una qualsiasi di esse, con la certezza di ottenere un errore inferiore a DF, e quindi a e. Inoltre, è noto anche il segno dell'errore, essendo F''<F<F'.

Esempio numerico. Si consideri un sistema "ponte" con componenti di affidabilità p =0.9900 (è importante in questa sede specificare la precisione numerica dei dati!). Dalla relazione generale del par. 7 si può ricavare che l'affidabilità del sistema risulta pari a R=0.9998, e quindi F = 1-R= 2E-4. Ipotizzando di non sapere (o non volere) svolgere il calcolo esatto, si può ricorrere alle relazioni approssimate, con il metodi dei cut-set.

Si può verificare (con un po' di abilità, anche senza calcolatrice) che: F' = 2.02E-4 e F'' = F' - 5E-8 - 1E-l0. In questo caso, dunque, F' e F'' sono praticamente uguali (la differenza è inferiore alla precisione dei dati), e quindi si può scrivere: F F'=2.02E-4, con un errore assoluto (per eccesso su F e per difetto su R) pari a 2E-6, veramente trascurabile L'errore percentuale su F risulta pari all'1%. Naturalmente l'errore su R è molto più piccolo, ed è pari al 2E-4 %!. Si noti che ciò è legato al valore elevato, 0.99, di p: per valori inferiori si otterranno degli errori più grandi.

5.8.4 Cenni sul metodo Montecarlo (o "simulazione stocastica")

Il metodo Montecarlo è un processo implementato al calcolatore che, impiegando algoritmi basati sulla generazione di numeri casuali, simula il comportamento casuale di un sistema da un punto di vista affidabilistico (esso è comunque adoperabile per tutti i sistemi di tipo aleatorio, ad esempio per risolvere il "Load-flow" probabilistico).

Dal punto di vista teorico, esso è basato sulla legge dei grandi numeri. Detto in maniera semplice, esso funziona - nel caso statico - come segue: si effettuano numerose prove (simulate) sul sistema, e se ne valuta l'affidabilità come percentuale di prove in cui il sistema ha funzionato. A differenza dei metodi fin qui visti, che sono probabilistici, esso è un metodo di carattere "statistico": infatti è ovvio che con tale metodo si riesce solo a stimare statisticamente (non a valutare analiticamente o numericamente, ossia con metodi analitici approssimati) l'affidabilità di un sistema.

Ad esempio, se si generano diverse sequenze di numeri casuali, ogni volta si avrà, in generale, un risultato diverso: in altri termini, il risultato di una stima Montecarlo è una variabile aleatoria, di cui si può calcolare la probabilità che sia prossima al valore "vero" dell'affidabilità (che rimarrà comunque incognito).

Tale metodo è quindi preferibilmente usato quando è impossibile - per la complessità del sistema da analizzare - utilizzare i procedimenti (esatti) di tipo probabilistico. Un grosso vantaggio del metodo è la sua relativa semplicità, mentre lo svantaggio pratico è legato alla durata del tempo-macchina necessaria a valutare sistemi complessi, dato che per ottenere stime affidabili bisogna in genere simulare diverse migliaia di prove. Naturalmente, il grosso svantaggio è di tipo teorico, non fornendo tale metodo risultati analitici, o di cui sia possibile valutare deterministicamente i margini di errore.

Da quanto detto si ricava che il metodo Montecarlo non è - a rigore - classificabile (come spesso - erroneamente - si fa in ambito ingegneristico) tra i "metodi di risoluzione" dei sistemi. Piuttosto, esso è un metodo di stima statistica. Naturalmente, esso è eseguito al calcolatore per motivi di tempo e economici. Nulla vieta - in principio - di usare tabelle di numeri casuali, o metodi "artigianali" (v. esercizio 8 più avanti).