MOMENTO ANGOLARE - LEGAME DEL MOMENTO ANGOLARE CON LE OPERAZIONI DI ROTAZIONE

MOMENTO ANGOLARE

Per una particella che si muove nello spazio, in meccanica classica, è definita la grandezza momento angolare come:

dove r(x,y,z) è il vettore posizione e p(p_x,p_y,p_z) il vettore quantità di moto. Analiticamente si ha:

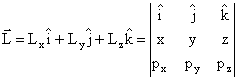
La generalizzazione immediata alla meccanica quantistica si ottiene sostituendo alla quantità di moto il corrispondente operatore vettoriale:

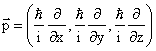
Si ottiene quindi:

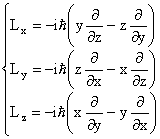
Il momento angolare così definito risulta essere un operatore hermitiano.

Analizziamo ora il problema della indipendenza delle componenti L_x, L_y e L_z. E' possibile misurare con precisione indipendente le componenti del momento angolare?

Calcoliamoci allora i commutatori di tali componenti[1]:

[L_x,L_y] = [yp_z zp_y , zp_x xp_z] = [yp_z , zp_x] [yp_z , xp_z] [zp_y , zp_x]+[zp_y , xp_z]

Per calcolare questi commutatori sfruttiamo delle importanti proprietà dell'operatore quantità di moto; infatti si può facilmente verificare che sia le componenti della quantità di moto fra loro sia le componenti del vettore posizione con le componenti non omologhe della quantità di moto commutano:

[p_x , p_y]=0    , [p_y , p_z]=0 , [p_x , p_z]=0

[x , p_y]=0    , [x , p_z]=0 , [y , p_x]=0 .

Inoltre, per le componenti omologhe vale:

[x ,p_x] = [y , p_y] = [z , p_z] =i

Quindi possiamo scrivere ad es:

[ yp_z , zp_x] = y[p_z,zp_x]+[y,zp_x]p_z = yz[p_z,p_x] y[p_z,z]p_x+z[y,p_x]p_z+[y,z]p_xp_z = y(-i)p_x = - iyp_x

Sfruttando le proprietà appena viste si ricava che:

[L_x , L_y] = iL_z

[L_z , L_x] = iL_y    (

[L_y , L_z] = iL_x

Si può osservare che la seconda e terza relazione si ricavano dalla prima permutando ciclicamente gli indici x, y e z.

Dalla (1) si deduce la relazione di indeterminazione che lega l'incertezza associata a misure di due componenti del momento angolare:

Componenti diverse del momento angolare non possono essere quindi misurate con precisione indipendente.

Se introduciamo l'operatore modulo quadro del momento angolare definito come:

L² = L_x² +L_y² +L_z²

Si può verificare che esso è hermitiano ed inoltre commuta con ciascuna delle componenti:

[L²,L_x] = 0 , [L²,L_y] = 0 , [L²,L_z] = 0

Possiamo pertanto scegliere come insieme rappresentativo di grandezze che caratterizzano il momento angolare il modulo quadro ed una componente. Convenzionalmente si sceglie la componente lungo l'asse z.

Un insieme completo di autofunzioni del momento angolare sarà costituito dalle autofunzioni di queste due grandezze. Chiamiamo queste autofunzioni j_l,m e identifichiamo gli autovalori  e a_z con e  (per motivi che saranno chiari in seguito):

(

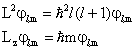l e m saranno reali perché L² e L_z sono hermitiani.

Analogamente a quanto fatto per l'oscillatore armonico cerchiamo di determinare i possibili valori degli indici l e m che abbiamo associato agli autovalori sfruttando le proprietà algebriche, ovvero le regole di commutazione delle componenti del momento angolare. Anche in questo caso possiamo introdurre degli operatori di innalzamento ed abbassamento:

L₊ = L_x+iL_y , L = L_x iL_y

Tali operatori si comportano rispetto ad L_z come gli analoghi operatori dell'oscillatore armonico nei confronti di H. Valgono infatti le seguenti proprietà di commutazione:

[L_z , L₊] = , [L_z , L ] =  (

In base alle (3) è facile mostrare che partendo da un autostato j_l,m di L_z (cioè j_l,m verifica la ( b )e applicando ad esso l'operatore di innalzamento si ottiene un altro autostato il cui autovalore ha l'indice incrementato di uno, ed applicando l'operatore di abbassamento si ottiene un altro autostato in cui l'indice dell'autovalore è diminuito di uno.

Dunque i nuovi autostati sono tali che:

L₊j_l,m j_l,m+1    e  L j_l,m j_l,m

A differenza però dell'oscillatore armonico questa scala ideale presenta un limite inferiore ed uno superiore. Per trovare questi limiti dobbiamo imporre che la norma degli stati decrementati o incrementati sia

L₊L = (L_x+iL_y) (L_x iL_y) = L_x² + L_y² i[L_x , L_y] = L² L_z² +L_z

Affinchè tale norma sia semidefinita positiva, il termine in m m²+m+l(l+1) dovrà essere maggiore o uguale a 0; ciò comporta che:

l m l+1

Ripetendo lo stesso ragionamento per lo stato incrementato si ottiene:

   T (l+1) m l

Le due condizioni saranno soddisfatte contemporaneamente se:

l m l

Poiché L₊ e L incrementano o decrementano m di 1, allora la scala da l a l sarà costituita di gradini interi e quindi la differenza tra l e -l , cioè 2l , sarà un valore intero.

Dunque l può assumere valori interi o semi-interi.

I valori semi-interi si possono escludere studiando le proprietà di trasformazione dello stato sotto operazioni di rotazione come vedremo nel paragrafo successivo.

Riassumendo, si hanno due numeri quantici l ed m, di cui l è un intero positivo ed è associato al modulo del momento angolare ed m è un intero che assume tutti i valori compresi tra l e l ed è associato alla componente del momento angolare nella direzione dell'asse z.

legame del momento angolare con le operazioni di rotazione

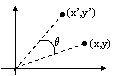Consideriamo un punto sul piano x,y di coordinate (x,y,0). Se ruotiamo la posizione del punto di un angolo q intorno all'asse z, le sue coordinate muteranno come segue:

Per piccole rotazioni q, cosq 1 e senq q quindi:

L'effetto di una rotazione sullo stato del sistema si può rappresentare tramite l'applicazione di un operatore unitario U_q che poniamo, in analogia con il caso delle traslazioni (vedi 8), nella forma:

Calcoliamo il valor medio della x e della y sullo stato ruotato:

Dall'ultima espressione possiamo togliere la coniugazione perché il valor medio è reale; e introducendo un nuovo operatore x(q) = si ha:

Dunque il valor medio della posizione sullo stato ruotato è pari al valor medio di x(q) sullo stato non ruotato.

La stessa cosa vale per l'operatore y, introducendo y(q) =.

Richiediamo ora che i valori medi si trasformino come le coordinate nel sistema classico sotto le rotazioni, e considerando piccole rotazioni si ottiene:

(

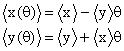Ma:

E analogamente, arrestandoci al primo ordine perché consideriamo piccole rotazioni:

Affinchè le (4) siano soddisfatte dovrà allora essere:

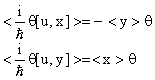ovvero: (

Ma un operatore che verifica le (5) è proprio L_z infatti:

[L_z , x] = [xp_y yp_x , x] = xp_yx yp_xx x²p_y + xyp_x = y[x,p_x] = iy

E analogamente [L_z , y] = ix

Quindi possiamo identificare l'operatore u con L_z.

L'operatore sarà allora un operatore di rotazione e L_z viene detto generatore delle rotazioni

Lo stesso ragionamento si può ripetere per rotazioni rispetto agli assi x e y.

Consideriamo ora uno stato derivante da una misura di L², cioè un autostato di L², con l fissato. Esso sarà dato da una sovrapposizione di autostati di L_z, con valori m che andranno da l a l:

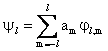
Se applichiamo a questo stato l'operatore di rotazione otteniamo:

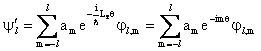
Otteniamo quindi una nuova sovrapposizione in cui ogni autostato è moltiplicato per un fattore di fase associato all'autovalore corrispondente di L_z.

Per una rotazione di 2p lo stato deve ritornare identico se le variabili posizionali sono gli unici gradi di libertà del sistema.

q p

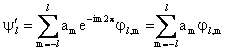
Questa uguaglianza è verificata solo se m assume solo valori interi e ciò ci conferma quanto avevamo anticipato nel paragrafo precedente.