2.10 PROBABILITÀ CONGIUNTA E PROBABILITA' CONDIZIONATA

2.10.1 Probabilità congiunta e "regola della catena"

La definizione di probabilità condizionata consente anche il calcolo della probabilità che due eventi si verifichino congiuntamente - ossia la probabilità dell'intersezione dei due eventi, detta anche "probabilità congiunta" - infatti:

P(A B) = P(B)P(A|B) = P(A)P(B|A) 

Come si ricava, rispettivamente dalle relazioni:

P(A|B) = P(A B) / P(B), e: P(B|A) = P(A B)/P(A).

Naturalmente, il 2° membro della (1) è definito solo se P(B) >0, il 3° membro solo se P(A) >0.

La (1) costituisce spesso la maniera più rapida di calcolare la probabilità congiunta, come illustrato nell'esempio che segue. In altri termini, anche se si utilizza la probabilità congiunta per definire la probabilità condizionata (come fatto al par. 2.9), in pratica è spesso - data la semplicità di calcolo e anche il significato intuitivo di probabilità condizionata - seguire, nei calcoli, il percorso inverso.

Esempio

Si consideri ancora l'esempio della estrazione a caso di due sectiune da un mazzo di sectiune napoletane (par. precedente), senza rimessa. Quale è la probabilità che entrambe siano assi?

Con gli stessi simboli adottati in precedenza, si tratta di calcolare la P(A B); ciò è facile, dato che è facile calcolare, come fatto in precedenza, le probabilità :

P(A) = P(la prima carta è un asso) = 1/10, e:

P(B|A) = P(la seconda è un asso, dato che la prima era un asso) = 3/39 = 1/13;

da cui:

P(A B) = 1/130

Si noti che P(B) = P(A) = 1/10 (vedi nota seguente), e quindi - come già detto - A e B non sono indipendenti nel caso di estrazione senza rimessa, essendo : P(A B) P(A)P(B) =1/100.

Si noti che, se le sectiune venissero rimesse nel mazzo dopo essere estratte, le estrazioni sarebbero naturalmente indipendenti, avendosi infatti: P(B|A) = P(B) = 1/10; quindi si avrebbe in tal caso: P(A B) = 1/100 (come intuitivo, la probabilità di estrarre due assi , con rimessa, è maggiore che nel caso senza rimessa). In entrambi i casi, gli stessi risultati possono essere ottenuti con il calcolo combinatorio, un po' meno facilmente rispetto all'utilizzo della probabilità condizionata, che proprio in tali applicazioni rivela la sua utilità.

Nota (teorema dell'estrazione casuale): qui, come in precedenza (esempio di . 28) si è dato per scontato il fatto che P(B) = 1/10; ora, P(B) rappresenta la probabilità che la seconda carta sia un asso, e dunque si tratta di una probabilità "non condizionata", ossia calcolata senza sapere l'esito della prima estrazione ( a differenza di P(B|A)). Il fatto che P(B) = P(A) = 4/40 può lasciare perplessi (comprensibilmente), se si pensa che all'atto della seconda estrazione i casi possibili sono 39, e non più 40. In realtà si ha proprio P(B) = 4/40, come si può dimostrare una volta introdotta la formula della "probabilità totale" (vedi "teorema dell'estrazione casuale", par. 2.12, es. 3). Il risultato può comunque essere accettato intuitivamente se interpretato soggettivamente: se io non conosco il risultato della prima estrazione, per me è come se i casi possibili fossero ancora 40, e quelli favorevoli 4 (nell'ipotesi di equiprobabilità qui assunta, la carta già estratta dal mazzo ha la stessa probabilità di essere una qualsiasi delle 40 iniziali, e quindi la sua estrazione non altera il mio stato di informazione). In altre parole, l'esito della prima estrazione, se incognito, non altera - anche senza rimessa - la probabilità di un evento collegato all'estrazione successiva, anche se le estrazioni successive - essendo senza rimessa - non sono indipendenti! Ancora più sorprendente può apparire il fatto che il ragionamento può essere esteso naturalmente ad ogni estrazione successiva, fino alla 40-sima: ad esempio, la probabilità che la 40-sima carta estratta dal mazzo sia un asso, senza conoscere l'esito delle precedenti 39 estrazioni, è sempre pari a 4/40, anche se i casi possibili sono (apparentemente) ridotti ad uno solo!

Un esempio analogo, più "pratico", è relativo alla lotteria: supponiamo che vengano messi in vendita 1000 biglietti di una lotteria, e di questi uno solo contenga il premio; dunque, se acquisto un biglietto, la mia probabilità di vittoria è di 1/1000, e questo anche se io sono il 1000-simo acquirente (purché io ignori i risultati dei precedenti 999 acquirenti), e dunque è rimasto un solo biglietto. Benché il ragionamento appena fatto sia del tutto corretto, pur non espresso in forma matematica ma "logica", esso appare - come sperimentato! - oscuro a molte persone estranee al campo scientifico (il lettore può proporre l'esempio a qualche suo amico per verificare ciò), come anche ad una buona percentuale di studenti che si imbattono per la prima volta nella probabilità , ed è una dimostrazione del fatto che la logica probabilistica spesso sembra fare a pugni con quella ordinaria (e vedremo altri esempi di ciò . ). La cosa non deve preoccupare, visto che spesso i problemi di probabilità hanno indotto in errore anche importanti scienziati!

Ribadiamo comunque che il ragionamento fatto, per quanto corretto, non è una dimostrazione.

Regola della "catena"

La relazione (1) può essere facilmente generalizzata a più eventi; ad esempio, nel caso di tre eventi si può scrivere:

P(A B C) = P(A)P(B|A)P(C|A B )

Il nome di questa regola è facilmente compreso: perché si verifichi l'evento congiunto ABC, costituito dai tre eventi A, B, C immaginati in successione - come appunto in una "catena" temporale - occorre che si verifichi A, quindi B dato A, infine C dati A e B. Naturalmente, la "catena" può partire da uno qualsiasi degli eventi (ad esempio, si può scrivere: P(A B C) = P(C)P(B|C)P(A|B C )), visto che in realtà la probabilità condizionata non implica necessariamente alcuna "successione temporale" degli eventi (v. anche nota in fine del sottoparagrafo che segue).

Per dimostrare la (2) si può partire dall'ultimo termine e applicare la definizione di probabilità condizionata: P(C|A B ) = P(A B C)/P(A B); esprimendo la probabilità congiunta a denominatore mediante la probabilità condizionata: P(A B) = P(A)P(B|A), si ha l'asserto.

Si noti che, naturalmente, per applicare la (2) è necessario che tutti gli eventi condizionanti (A e A B) abbiano probabilità diversa da zero (in pratica, è sufficiente che A B abbia probabilità diversa da zero; perché?). La formula è analogamente estensibile ad un qualsiasi numero di eventi.

Esempio

Con riferimento all'esempio delle sectiune, la probabilità di estrarre 3 assi nelle prime tre estrazioni senza rimessa si può calcolare, applicando la (2) - così:

P(A B C)=(1/40)(3/39)(2/38) = 1.01E-4

Per quanto detto in precedenza, questa è anche la probabilità di estrarre 3 assi in tre estrazioni successive qualsiasi (non necessariamente le prime tre), se non si conosce il risultato delle precedenti estrazioni (purchè si sappia che si sono già estratte non più di 37 sectiune!).

Nelle stesse ipotesi, la probabilità di estrarre 5 assi consecutivi è ovviamente nulla: volendo formalizzare questo fatto si può procedere in due modi:

detti (A,B,..,E) i cinque eventi consecutivi, la loro intersezione è chiaramente un evento impossibile (si noti che però essi non sono incompatibili, in quanto non lo sono a due a due!);

applicando la regola della catena ai cinque eventi, partendo da A, si vede subito che P(E|A B C D) = 0, perché dopo la quarta estrazione favorevole non ci saranno più assi.

Anche quest'esempio mostra l'utilità dell'uso della probabilità condizionata ai fini del calcolo della probabilità congiunta (ai più, il metodo 2) appare più immediato del metodo 1)).

Domanda: Nelle stesse ipotesi, si calcoli la probabilità di estrarre almeno un asso in tre estrazioni (suggerimento: conviene calcolare prima la probabilità dell'evento complementare . )

2.10.2 Probabilità "inversa"

Nota la P(B|A), è possibile - se sono note la P(A) e la P(B) - anche ricavare la cosiddetta "probabilità inversa", P(A|B); dalla relazione (1) si ricava infatti:

(3)

Si noti che tale relazione non rappresenta un nuovo "teorema", ma è solo un modo diverso di scrivere la probabilità condizionata: P(A|B) = P(A B)/P(B), scrivendo la probabilità congiunta a numeratore in funzione dell'altra probabilità condizionata P(B|A).

Esempi

1. (Diagnostica e Affidabilità). Un esempio notevole di utile applicazione della (3) è quello relativo ai problemi di diagnostica in affidabilità. Se B è un evento relativo al funzionamento (o guasto) di un sistema, e A è un evento relativo al funzionamento (o guasto) di un componente di tale sistema, è spesso molto semplice calcolare la probabilità P(B|A). A fini diagnostici, o di manutenzione, è molto importante il calcolo della probabilità "inversa" P(A|B); ad esempio, se:

B = [il sistema è guasto]; A_i = [il componente ai è guasto],

il calcolo delle probabilità P(A_i |B) ci consente di individuare, una volta saputo che il sistema è guasto, quale tra i componenti è - con maggior probabilità - guasto (diagnosi) e quindi su quale intervenire per primo, ai fini della riparazione o manutenzione del sistema.

Ad esempio, se il nostro è un sistema serie, P(B|A_i ) = 1, ovviamente (se è guasto un qualsiasi componente, il sistema si guasta: si noti che tale relazione è stabilita per via intuitiva; naturalmente, lo stesso risultato lo si trova col calcolo, osservando che il guasto del sistema serie è dato, in termini di evento, dalla unione degli eventi di guasto relativi ai componenti), da cui si ha semplicemente, ai fini del calcolo delle probabilità "inverse":

P(Ai |B) = P(Ai)|P(B)

(Ripetere l'esempio per un sistema parallelo)

Applicazioni analoghe si ritrovano nell'ambito della diagnostica medica.

2. (Calcio) Si consideri ancora l'esempio calcistico visto a proposito della probabilità condizionata, in cui una squadra "a" gioca una partita di calcio contro un'altra squadra "b", e sia: A = [a vince la partita], V = [a è in vantaggio al termine del primo tempo]; in assenza di informazioni, assumiamo:

P(A) = P(V) = 1/3, e ipotizziamo che sia - come nell'esempio di cui sopra - P(A|V) = 2/3 = 2P(A). Supponiamo ora di conoscere solo il risultato finale, sia A, e di chiederci quale sia la probabilità che la squadra A abbia terminato in vantaggio anche il primo tempo; si ha:

P(V|A) = P(V)P(A|V)/P(A) = P(A|V) = 2/3

Cioè: se io so che "a" ha vinto la partita, la probabilità che abbia vinto anche il primo tempo è pari a 2/3 (*).

Più in generale, indipendentemente dai valori di P(A) e P(V), potendosi scrivere:

P(V|A)/ P(V) = P(A|V)/P(A)

Si può affermare che se P(A|V) = 2P(A), allora anche P(V|A) = 2P(V).

(*)Nota: Come si vede in questo esempio, la probabilità condizionata di A all'evento B non presuppone - come a volte si crede - che l'evento B si verifichi prima di A; in questo caso, l'evento V=[a ha vinto il primo tempo] è precedente all'evento A=[a ha vinto la partita], e tuttavia è del tutto lecito - se non si conosce l'esito del primo tempo, ma solo il risultato finale - chiedersi quale sia la P(V|A). Questo fatto pure lascia perplessi alcuni, che obiettano (giustamente) che il risultato del primo tempo non dipende da quello finale: tale obiezione si basa però su un concetto improprio di probabilità condizionata; infatti la probabilità condizionata P(A|B) esprime semplicemente come cambia il nostro stato di informazione riguardo ad A, avendo saputo B si è verificato, e non implica un rapporto di "causa-effetto", né una qualsiasi relazione o consecutio temporale, tra i due eventi. Quindi, è possibile chiedersi quale sia la probabilità di un evento passato (ma incognito, ovvero incerto), sulla base della conoscenza di un evento presente; ad esempio, è questo che spesso fanno gli archeologi, gli storici, ecc.

In altri termini, non è corretto dire che la probabilità P(A|B) è la probabilità di A dopo che si è verificato B; ovvero, la successione temporale non è tra A e B, ma tra le nostre conoscenze riguardo al verificarsi di A e B.

2.11 PROPRIETA' NOTEVOLI DELL'INDIPENDENZA STATISTICA

2.11.1 Indipendenza e Probabilità Condizionata

Può essere utile riprendere il concetto e la definizione di eventi statisticamente indipendenti, alla luce della probabilità condizionata. Si è già visto che, se A e B sono indipendenti (si omette spesso implicitamente l'avverbio "statisticamente"), si ha, utilizzando la definizione di indipendenza:

P(A|B) = P(A) e P(B|A) = P(B) (1)

Come già detto, P(A|B) = P(A) esprime il fatto dire che il verificarsi dell'evento B non ha alcuna influenza sulla probabilità di verificarsi di A (ovvero non cambia le informazioni in nostro possesso su tale probabilità), e ciò chiarisce meglio il significato di indipendenza. Se P(A|B) = P(A), siamo portati a dire che "A è indipendente da B" ( e non che "B è indipendente da A"). Ma, in base a quanto visto a proposito della "probabilità inversa", le due relazioni che compaiono nella (1) sono del tutto equivalenti. Cioè, se P(A|B) = P(A), anche P(B|A) = P(B), come si vede facilmente.

In altri termini, se "A è indipendente da B", anche "B è indipendente da A", e viceversa. La definizione di indipendenza, data in termini di probabilità congiunta, chiarisce in effetti la "simmetria" della proprietà.

Viceversa, se è valida una qualsiasi delle (1), si verifica che A e B sono indipendenti; dunque, una qualsiasi delle (1) può essere assunta come definizione alternativa di indipendenza. In definitiva, si ha la seguente notevole proprietà:

Proprietà (definizioni alternative di indipendenza)

Due eventi sono statisticamente indipendenti se, e solo se, vale una qualsiasi delle seguenti proprietà:

P(A B) = P(A)P(B), oppure: 2. P(A|B) = P(A), oppure: 3. P(B|A) = P(B) (2)

nel senso che ognuna delle tre implica le altre due.

La definizione di indipendenza in termini di probabilità congiunta, che è quella che si è data nel par. 2.9, è più generale da un punto di vista matematico, perchè non esclude - a differenza delle altre - eventi di probabilità nulla. La verifica dell'indipendenza è però spesso più intuitiva se effettuata in termini di probabilità condizionata.

Nel caso di più eventi, le formule si generalizzano semplicemente (v. regola della catena). Ad esempio, nel caso di 3 eventi (A,B,C), asserire l'indipendenza equivale, in termini di probabilità condizionata, a verificare che una qualsiasi combinazione di eventi condizionanti (cioè "a denumeratore") non altera la probabilità dell'evento condizionato (cioè " a numeratore"), ad esempio:

P(A|B) = P(A), P(A|B C) = P(A), .    (3)

e quelle analoghe che si ottengono considerando anche B e C come eventi condizionati.

2.11.2 Indipendenza e incompatibilità

Molto spesso, e anche questo è un fatto sperimentato .. statisticamente, si fa confusione tra il concetto di incompatibilità e quello di indipendenza. Tale confusione è più che altro semantica, cioè legata al significato delle parole, e non certo legata alle definizioni, che sono molto chiare. Innanzitutto va detto che le due definizioni non hanno nulla a che vedere l'una con l'altra!

Facendo riferimento al caso di due eventi, ricordiamo infatti che:

due eventi A e B si dicono incompatibili se A B = : l'incompatibilità è dunque una proprietà legata agli eventi; in essa - a differenza che con l'indipendenza - non e la probabilità ! (si ricordi che essa è stata infatti introdotta prima di quella di probabilità )

l'indipendenza (P(A B)= P(A)P(B)), non è invece una proprietà intrinseca, ma dipende dalla probabilità degli eventi, per cui la si può evincere solo dal calcolo.

Dunque, come chiariremo con degli esempi, gli stessi eventi possono essere indipendenti o meno a seconda della misura di probabilità assegnata allo spazio campione; poiché la misura di probabilità viene a volte assegnata soggettivamente, sulla base dell'informazione che si ha sugli eventi, anche l'indipendenza può avere un aspetto soggettivo (a differenza della incompatibilità: una volta assegnato lo spazio campione, due eventi o sono incompatibili o non lo sono, ciò non dipende dallo stato di informazione, che influenza invece la probabilità e quindi l'indipendenza). Ad esempio, l'incompatibilità può essere dedotta dai diagrammi di Venn (si hanno due insiemi privi di punti in comune), l'indipendenza no!

Vediamo ora una frequente (e dunque .. probabile!) affermazione riguardo al rapporto tra le due proprietà: 'Due eventi incompatibili, non avendo alcun punto in comune, sono indipendenti". Qui si intende evidentemente che i due eventi "non hanno nulla a che fare" l'uno con l'altro, e quindi debbono essere indipendenti . Tale affermazione è, per quanto a prima vista ragionevole, del tutto sbagliata. Infatti, l'unica regola di carattere generale che lega le due proprietà è la seguente, molto semplice, che afferma proprio il contrario, e cioè che: "se si escludono gli eventi nulli, l'incompatibilità esclude l'indipendenza"; ciò è in effetti ovvio, se si ragiona correttamente in base al significato intuitivo di indipendenza .

Proprietà (Dipendenza degli eventi incompatibili). Se due eventi A,B - aventi probabilità positiva - sono incompatibili, sono anche (statisticamente) dipendenti; due eventi incompatibili sono invece indipendenti se e solo se P(A) oppure P(B) sia uguale a zero

(Nota: chiamiamo, chiaramente, "dipendenti", eventi che non sono indipendenti. La definizione va naturalmente interpretata probabilisticamente, nel senso di modifica della informazione riguardo alla probabilità , e non implica un rapporto di dipendenza logica o di causa-effetto tra i due eventi).

La verifica è immediata: se A e B sono incompatibili, P(A B) = P( ) = 0, e questo coincide con il prodotto delle probabilità di A e B se e solo se almeno una delle due è nulla.

Oppure, in termini di probabilità condizionata: se A e B sono incompatibili - deve essere (supponiamo P(B) > 0 in modo da poter condizionare): P(A|B) = 0; perché A e B siano indipendenti deve essere P(A|B) = P(A). Allora, se P(A) = 0, tali eventi incompatibili sono indipendenti, e analogo ragionamento vale a partire dalla P(B|A), se P(A) > 0.

Se si interpreta correttamente il concetto di indipendenza, in rapporto all'informazione, il fatto che eventi incompatibili aventi probabilità diversa da zero non siano indipendenti è ragionevole: infatti, se si verifica uno dei due (ad esempio B), siamo sicuri che l'altro, A, non si verifica, e quindi la nostra informazione cambia drasticamente, come ad esempio nell'es. seguente.

Esempio 1 (Eventi incompatibili e dipendenti)

Si consideri l'esperimento aleatorio E "lancio di una moneta"; gli eventi T= e C= sono (in)compatibili e (in)dipendenti?

T e C sono ovviamente incompatibili perché T C= , e quindi P(T C) = P( ) = 0 (si noti che l'incompatibilità vale nello stesso lancio, nel quale inevitabilmente o esce testa, o esce croce; è chiaro che in lanci diversi si possono avere sia T che C).

Se riteniamo P(T) e P(C) non nulle, T e C non sono indipendenti. Ad esempio, nel caso di probabilità uniforme, si ha P(T C) P(T)P(C) = 1/4.

Come si vede, una volta appreso il verificarsi dell'evento T, passiamo da una assegnazione iniziale di probabilità: P(C) = 0.5 > 0, ad una assegnazione nulla: P(C|T) = 0. Proprio in tale cambiamento risiede la dipendenza. In definitiva, se due eventi di probabilità positiva sono incompatibili, non solo non sono indipendenti, ma sono in un certo senso dipendenti al "massimo grado", dato che uno esclude l'altro. Se invece uno dei due eventi incompatibili ha probabilità nulla, sia A, il fatto che si verifichi B non muta le nostre informazioni sulla probabilità di A, avendosi P(A|B) = 0 = P(A), e questo è il motivo per cui in tal caso gli eventi incompatibili sono anche indipendenti. Un caso notevole è quello dell'evento impossibile, che è indipendente da qualsiasi altro evento (es. seguente).

Esempio 2 (Eventi incompatibili e indipendenti)

Sia A un qualsiasi evento di W; si verifichi che e A sono incompatibili e indipendenti.

E' ovvio che i due eventi sono incompatibili, in quanto A , qualunque sia A.

Poiché P( ) = 0, essi devono essere anche indipendenti, infatti P(A ) = P( ) = 0 = P(A)P(

In particolare, anche W e sono indipendenti tra di loro.

Spiegazione logica: l'evento impossibile ha sempre probabilità nulla, qualsiasi altro evento si verifichi non può mutare la sua probabilità condizionata rispetto a quella " a priori".

Domande

1. Si verifichi che anche l'evento certo è indipendente da qualsiasi altro evento, e se ne spieghi il perché a parole.

Si verifichi, analogamente, che un evento nullo (non necessariamente l'evento impossibile!) è indipendente da qualsiasi altro evento; si faccia lo stesso per un evento "quasi certo". (Nota: la verifica non è semplicissima..).

Consideriamo ora eventi compatibili. Potrebbe sembrare intuitivo che, se due eventi sono compatibili, non siano indipendenti, dato che hanno degli elementi in comune; ma anche questo non è vero, in generale. Ma non è vero neanche che sono sempre indipendenti: tutto dipende dalla assegnazione di probabilità su tali eventi, come detto inizialmente. Il lettore consideri gli esempi che seguono e cerchi di motivare perché una volta due eventi compatibili sono indipendenti (Es. 3), e l'altra (Es. 4) gli stessi eventi (!) sono dipendenti.

Esempio 3. (Eventi compatibili e indipendenti)

Sia E l'esperimento aleatorio "lancio di un dado"; sia inoltre A=, B=. Dimostrare nell'ipotesi di probabilità uniforme, che A e B sono indipendenti.

Nel caso in esame, W = ; è ovvio che A e B sono compatibili, infatti A B = . Ora non resta che verificare la definizione di indipendenza:

P(A) = 1/3; P(B) = 1/2; P(A B) = 1/6 = P(A)P(B) T A e B sono indipendenti.

Esempio 4. (Eventi compatibili e dipendenti)

Si consideri lo stesso esperimento aleatorio del caso precedente, considerando, però, un ipotetico dado a 5 facce. Dimostrare che stavolta gli stessi eventi A e B sono, oltre che compatibili, dipendenti

Stavolta: W = ; (A B)=;

P(A) = 2/5; P(B) = 3/5; P(A B) = 1/5 P(A)P(B) T A e B sono dipendenti.

Si osservi che, rispetto all'es. precedente, è cambiata la misura di probabilità sugli eventi. In effetti, qui è cambiato anche lo spazio campione, ma ciò non è indispensabile: si potrebbe pensare ad un dado ancora a 6 facce, ma "truccato" in modo che il 6 non esca "quasi" mai (ossia abbia probabilità nulla), e gli altri numeri siano equiprobabili.

In definitiva, incompatibilità e indipendenza sono proprietà che non hanno alcuna relazione l'una con l'altra, se non nel caso - peraltro molto particolare - di eventi nulli o quasi certi (che sono eventi che non capitano.. quasi mai nelle applicazioni dell'ingegneria).

2.12 Teorema della probabilità totale

2.12.1. Caso di due eventi condizionanti

Il teorema della probabilità totale costituisce uno strumento molto utile: esso viene usato quando si vuole calcolare la probabilità di un evento A, conoscendo P(A|B) e P(A|), una volta che sia nota la P(B). Infatti, considerati due qualsiasi eventi A e B, si può scrivere la già nota relazione di decomposizione: A= (A B) (A ); essendo (A B) e (A ) incompatibili, si può scrivere: P(A) = P(A B) + P(A ), da cui, utilizzando le probabilità condizionate note, P(A|B) e P(A|):

(1)

In pratica, P(A) viene ad essere una "media pesata delle probabilità condizionate P(A|B) e P(A|), i pesi essendo costituiti rispettivamente da P(B) e P(). Anche la (1) è di semplice interpretazione intuitiva: la probabilità che si verifichi A è uguale alla probabilità che si verifichino B e A dato B, più quella che si verifichino e A dato .

Esempio 1 (affidabilità di una linea elettrica)

L'affidabilità di una certa linea elettrica di trasmissione in un intervallo di tempo Dt è pari a 0.99 in condizioni climatiche favorevoli, e 0.82 in condizioni climatiche avverse. Si suppone (come è pratica comune, anche presso l'ENEL) che tutte condizioni atmosferiche si possano ricondurre a questi soli due stati, e che nell'intervallo Dt le condizioni atmosferiche non varino. Calcolare l'affidabilità della linea in tale intervallo, sapendo che la probabilità che in esso vi sia tempo favorevole (TF) è 0.98, e la probabilità che vi sia tempo avverso (TA) è 0.02.

Sia S l'evento "buon funzionamento" del sistema costituito dalla linea in esame. Gli eventi "TF" e "TA" sono per ipotesi l'uno il complementare dell'altro (si dice anche che sono "incompatibili ed esaustivi", v. appresso), con probabilità note, e si ha per ipotesi:

P(S|TF) = 0.99;  P(S|TA) = 0.82;

dunque, nel tempo Dt in esame, l'affidabilità della linea vale:

P(S) = P(TF)P(S|TF) + P(TA)P(S|TA) = (0.98)(0.99) + (0.02)(0.82) = 0.9866.

Si noti che il risultato è un valore compreso tra 0.82 e 0.99, e molto vicino a quest'ultimo, dati i valori di probabilità di TA e TF.

In generale, è facile dimostrare che, in base alla (1):

min P(A) max

Esempio 2 (affidabilità di una sistema elettrico con carico aleatorio)

E' noto che il carico elettrico di un dato sistema nel tempo futuro va previsto statisticamente - e così fa anche l'ENEL per i nostri consumi casalinghi, ai fini della tariffazione - in quanto esso costituisce, come già esemplificato nel cap. 1, un esempio di "variabile aleatoria". Dunque, per effettuare l'analisi di affidabilità di un sistema elettrico - intesa come probabilità di alimentare il carico - è necessario in genere conoscere la probabilità che il carico assuma determinati valori. Un semplice esempio di tale calcolo, che costituisce una naturale applicazione della probabilità totale, è il seguente:

Un sistema di generazione dell'energia elettrica è composto da due generatori di taglia 100 MW, connessi in parallelo alle sbarre del nodo di generazione, il quale fornisce potenza ad un sistema il cui carico complessivo è caratterizzato - in un certo intervallo di tempo futuro - da una punta di carico W che può assumere valori nell'intervallo (0, 200 MW). Detti A e B rispettivamente gli eventi:

A = (0 < W < 100); B = (100 < W < 200)

È noto, sulla base di statistiche sui consumi passati, di previsione del "trend" dei consumi, ecc., che tali eventi hanno probabilità: P(A) = 0.80; P(B) = 0.20. Calcolare l'affidabilità del sistema di generazione nel dato intervallo, nelle ipotesi:

a)  il funzionamento di ogni generatore è statisticamente indipendentemente dall'altro, e anche dagli eventi A e B (ossia dal "carico").

b)  Ogni generatore ha affidabilità- nell'intervallo in esame - pari a p = 0.9900.

Il semplice calcolo è lasciato al lettore; il risultato è: P(S) = 0.9960. Il lettore rifletta sulla ipotesi che generazione e carico siano statisticamente indipendenti.

Si noti che il sistema, in presenza di carico aleatorio, non è né serie né parallelo: sarebbe parallelo se si verificasse A, serie se si verificasse B, ma noi non sappiamo quale dei due eventi si verificherà. Però, conoscendo le probabilità di A e di B (che sono per ipotesi complementari), possiamo comunque calcolare P(S).

Dai precedenti esempi è chiaro come la probabilità totale sia uno strumento in pratica indispensabile quando si è incerti circa le condizioni in cui si svolge l'esperimento (ad es., le condizioni ambientali dell'es. 1, i valori di carico dell'es. 2, ecc.); mediante il "condizionamento", espresso dalle probabilità condizionate che appaiono nella (1), in pratica si riduce tale incertezza. Una tipica applicazione è quella cosiddetta di estrazione "da urna incognita", illustrata nel prossimo esempio, che esprime sotto forma generale il risultato già visto a proposito della estrazione di una seconda carta senza rimessa, senza conoscere l'esito della prima estrazione. Per maggiore chiarezza espositiva, il problema viene posto direttamente in forma soggettiva (il protagonista è il lettore, cioè .. tu), ma naturalmente il risultato è vero anche da un punto di vista "classico" o "frequentista" (riflettere sul perché di ciò dopo aver sviluppato l'esempio).

Esempio 3 (Teorema dell'estrazione casuale). Da un'urna contenente N palline, di cui b bianche e r rosse (con b + r = N, e N 2), vengono estratte a caso, in successione, 2 palline, senza rimessa. Tu sei chiamato a estrarre la seconda pallina, senza sapere il colore della prima estratta. Quale è la probabilità che tu estragga una pallina bianca? (Provare prima a dare una risposta intuitiva, e poi leggere il seguito; esaminare un caso numerico, ad esempio con N=2, b=r=1)

Osserviamo che, introdotti gli eventi casuali: B₁=[pallina bianca alla prima estrazione]; R₁=[pallina bianca alla prima estrazione], B₂=[pallina bianca alla seconda estrazione], si vuol sapere la P(B₂); per l'ipotesi di estrazione casuale, tutte le palline hanno la stessa probabilità di essere estratta: si noti che tale probabilità comune vale 1/N alla prima estrazione, e 1/(N-l) alla seconda, dato che le estrazioni sono senza rimessa. (Naturalmente, se l'estrazione fosse con rimessa, si avrebbe banalmente P(B₂)=b/N). Dunque, sono note le probabilità condizionate:

P(B₂ |B₁) = (b-l)/(N-l); P(B₂ |R₁) = b/(N-l).

Inoltre, gli eventi B₁ e R₁ sono ovviamente incompatibili ed esaustivi, e le loro probabilità sono valutabili come:

P(B₁) = b/N; P(R₁) = r/N = (1- b/N)

Da cui, applicando il teorema della probabilità totale:

P(B₂) = (b/N) [(b-l)/(N-l)] + (r/N) (b/(N-l); mettiamo in evidenza b/N e vediamo che succede:

P(B₂) = (b/N) [ (b-l)/(N-l) + r/(N-l) ] = (b/N) [(N-l)/(N-l)] = b/N. Si ha dunque il notevole risultato:

P(B₂) = P(B₁) = b/N

come nel caso con rimessa! Esso può apparire sorprendente, se si considera che alla seconda estrazione il numero di palline nell'urna è N-l, e non N, ma è stato già spiegato intuitivamente.

Naturalmente, applicando lo stesso metodo è possibile ottenere lo steso risultato per P(B₃), stavolta condizionando rispetto a B₂, e così via per B_4, B_{5, . .,} B_b.

Domanda: e che succede se non sappiamo quante estrazioni sono state fatte in precedenza (ma sappiamo che sono meno di b)? . Provare a dare una risposta intuitiva, ammesso che esista una risposta . ; se si vuole poi utilizzare il calcolo, è necessario utilizzare il teorema della probabilità totale nella forma più generale, esposto di seguito.

2.12.2. Caso generale (più di due eventi condizionanti)

Il teorema si può generalizzare a più eventi condizionanti nel seguente modo:

Siano _j=1,,n n eventi incompatibili, ed esaustivi, cioè la loro unione dà l'evento certo: (un caso particolare è quello di n=2, già visto prima, in cui un evento è complementare dell'altro) . Qualunque sia n, risulta allora, con una immediata generalizzazione della (1):

   (2)

purché le probabilità condizionate a secondo membro siano definite (ovvero tutte le probabilità degli eventi B_j siano positive). La dimostrazione è analoga a quella del caso di sue eventi: si scrive A come intersezione di A con l'evento certo, quest'ultimo come unione degli eventi B_j , e infine si calcola la probabilità di A utilizzando la proprietà distributiva e il terzo assioma.

Si noti che la condizione che gli eventi condizionanti siano incompatibili ed esaustivi vuol dire che uno e uno solo di essi si verifica. Infatti la condizione : vuol dire che almeno uno di tali eventi si deve verificare, mentre la condizione di incompatibilità impone che al più uno se ne verifichi (si ricordi che più di due eventi sono incompatibili se lo sono a due a due). Anche qui è facile verificare che P(A) è compresa tra la più piccola e la più grande delle probabilità condizionate a secondo membro.

Esempio 4 (affidabilità di una sistema elettrico con carico aleatorio - 2a parte)

Si consideri ancora il sistema di generazione dell'energia elettrica dell'Es. 2.. Supponiamo di sapere, sempre relativamente allo stesso intervallo di tempo futuro che stavolta la punta di carico W possa assumere valori nell'intervallo (0, 300 MW). Si considera dunque anche possibile l'evento:

C = (200 < W < 300)

Con gli stessi simboli adoperati in precedenza, si suppongono note le probabilità:

P(A) = 0.80; P(B) = 0.15; P(C) = 0.05.

Calcolare l'affidabilità del sistema di generazione nel dato intervallo, la sciando inalterate le altre ipotesi e dati.

Gli eventi A,B, C rispettano le ipotesi per l'applicazione della probabilità totale, se si suppone che il carico non possa superare i 300 MW (altrimenti gli eventi A,B,C non sarebbero esaustivi; naturalmente, la somma delle probabilità di eventi esaustivi deve essere uguale ad 1, come succede nel nostro caso); se non si conosce il limite superiore dei possibili valori di carico, bisognerà considerare come terzo evento condizionante, C, l'intervallo da 200 MW fino all'infinito.

Le probabilità di A,B, C, sono note, ed è semplice anche calcolare le probabilità condizionate:

P(S|A) = 0.9999; P(S|B) = 0.9801; P(S|C) = 0 (osservando che la missione del sistema è di alimentare il carico complessivo; naturalmente, se il carico è somma di più carichi singoli, quando il carico complessivo supera 200 MW sarà in genere possibile distaccare qualcuno di essi in modo che il sistema continui a funzionare, in modalità "ridotta". Ma qui, in una logica "binaria", anche questo evento andrebbe considerato come "guasto").

Dunque:

P(S) = P(A)P(S|A) + P(B) P(S|B) + P(C)P(S|C) = 0.9469.

Si noti che:

- il risultato è compreso tra la minima (0) e la massima (0.9999) delle probabilità condizionate (fatto teorico, che tra l'altro, se queste fossero vicine, potrebbe essere utilizzato per calcolare per lo meno un intervallo di valori possibili per P(S));

- il terzo termine P(C)P(S|C) è nullo, ma non possiamo dire che non conti.. nulla! Infatti - si veda anche quanto detto sopra - stavolta l'affidabilità del sistema si riduce drasticamente rispetto al valore (0.996) dell'esempio 2 (perché?). Ciò dimostra che una previsione accurata dei valori di carico è molto importante se non si vogliono compiere delle stime di affidabilità completamente errate (fatto pratico).

L'esempio che segue mostra come le ipotesi di applicazione della probabilità totale non siano tanto banali. E' molto importante cercare di dare una risposta prima di leggere la "soluzione".

Esempio 4 (Cautela nella applicazione della probabilità totale!)

Si supponga di voler calcolare l'affidabilità, P(S), di una sistema elettrico - formato da più componenti - ipotizzando di conoscere i seguenti dati:

un dato componente, c, del sistema si può guastare o per circuito aperto (c.a.), evento A, o per corto circuito (c.c.), evento B.

Entrambi tali eventi, supposti gli unici guasti possibili per il componente, possono comportare il guasto del sistema, evento G, con probabilità note.

Ci si chiede se e come si possa calcolare l'affidabilità del sistema.

Per ipotesi, sono note le pr: P(A) = P(c si guasta per c.a.), P(B) = P(c si guasta per c.c.), e le probabilità condizionate di guasto del sistema: P(G|A) e P(G|B). Si potrebbe allora pensare di calcolare l'inaffidabilità, P(G), del sistema, come segue:

P(G) = P(A)P(G|A) + P(B)P(G|B)

E quindi l'affidabilità come P(S) = 1 - P(G).

La precedente relazione, per quanto a prima vista corretta, è sbagliata! Infatti gli eventi A e B sono certo incompatibili, ma non esaustivi!. Il lettore spieghi perché e come si possa "correggerla" (naturalmente, aggiungendo eventuali ipotesi o dati mancanti, se è il caso).

La probabilità totale, se ben applicata!, è uno strumento fondamentale per il calcolo dell'affidabilità dei sistemi, e di ciò si vedranno altre applicazioni più avanti.

Per finire, si considerano degli esempi più . divertenti, ma comunque molto istruttivi, legati al gioco (in effetti, per molti, tali problemi sono di comprensione meno immediata rispetto alle applicazioni più strettamente ingegneristiche; per questo spesso sono i più utili per capire il concetto di probabilità ).

Esempio 5 (Gioco del Totocalcio)

Una persona gioca un simbolo (1, X, 2) per indovinare il risultato - tra i tre possibili - di una partita di calcio. Si ipotizzi che il simbolo, indipendentemente dalla partita considerata, venga scelto "a caso" (ossia con probabilità uniforme: ad esempio, si può supporre che il giocatore - non conoscendo affatto le squadre, o non intendendosi di calcio - lanci un dado e scelga "1" se esce 1 oppure 2, scelga "X" se esce 3 oppure 4, scelga "2" se esce 5 oppure 6).

a) Si verifichi che la probabilità , p, che il giocatore indovini il risultato di una partita è pari ad 1/3, indipendentemente dalle probabilità effettive dei 3 possibili risultati.

b) Quale è la probabilità P che, giocando in questo modo una "colonna" di 13 risultati, si "faccia 13" (cioè li si indovinino tutti)?.

a) il fatto che la probabilità p valga 1/3 appare immediato, ma forse non lo è tanto se si assume che i 3 risultati (1,X,2) non siano equiprobabili (e in effetti, normalmente essi non lo sono). In effetti, se i simboli sono scelti in maniera equiprobabile, ossia "a caso", il risultato p =1/3 rimane valido, come suggerito dal testo, indipendentemente dalle probabilità effettive dei 3 possibili risultati (persino se uno dei 3 ha probabilità nulla!). Il lettore può verificarlo utilizzando ancora la probabilità totale. Come?

b) una volta accertato il punto a), applicando la regola della catena e utilizzando l'ipotizzata indipendenza delle scelte dei simboli, è chiaro che:

P = p¹³ = (1/3)¹³

Tale risultato può essere ritrovato anche con il calcolo combinatorio (v. Cap. 3, al quale si rimanda per altri esempi sull'argomento), essendo 3¹³ il numero di possibili risultati diversi di una schedina (ovvero, questo è il numero di "13 triple"). Il risultato è valido nell'ipotesi in cui i risultati siano equiprobabili, e quindi si possa applicare la definizione classica di probabilità . In effetti, i due modi di procedere non sono diversi, se si pensa che, per chi gioca a caso, è come se i 3 risultati di ogni partita fossero equiprobabili, anche se non lo sono! Si noti che anche in questo esempio si trova un legame tra l'assegnazione uniforme di probabilità e l'indipendenza degli eventi, come nell'Es. di . 25 (lanci di una moneta).

Esempio 6 (Giochi . truccati: esempio della "moneta incognita")

Per tale esempio prendiamo spunto dalla cronaca, che nel Gennaio del 1999 ha proposto all'attenzione del pubblico delle frodi riguardo alle estrazioni del lotto. Supponiamo dunque che le probabilità di estrazione dei 90 numeri vengano alterate, ad esempio - tanto per fare un esempio semplice - perché un numero, x, viene tolto, ossia omesso dall'estrazione, (cosicchè la probabilità che x sia estratto diviene nulla, mentre gli altri hanno probabilità 1/89). Ci si chiede: "se non si conosce il numero x, quanto vale la probabilità di uscita, p(y), di un qualsiasi numero y tra i 90 del lotto"?

Dovrebbe essere abbastanza chiaro, con ragionamenti analoghi a quelli fatti a proposito della "estrazione della seconda carta", che la p(y) vale sempre 1/90 (anche se y = x!, ma si noti che supponiamo di non conoscere x). Da ciò si può anche dedurre che - per chi punta su certi numeri in una singola estrazione truccata, senza conoscere il meccanismo del trucco (qualunque sia il trucco, anche più sofisticato di quello qui esemplificato), la probabilità di vittoria rimane inalterata! Anche questo risultato può apparire sorprendente (immaginate di raccontarlo a qualcuno che ha perso un bel po' di soldi giocando su numeri che, a posteriori, si è visto che non potevano uscire!), ma si dimostra facilmente con la probabilità totale. Il meccanismo è ancora quello visto proposito delle "estrazioni da urne incognite", e può essere compreso facilmente se si considera il seguente esempio, più semplice ma del tutto analogo:

"Viene lanciata una moneta incognita (cioè ignoriamo se e come è stata truccata), ci viene solo detto che uscirà testa oppure croce. Volendo scommettere sul risultato, come valutiamo la probabilità che esca testa?"

Vi sono evidentemente 3 casi possibili rispetto alla composizione della moneta:

B₀ = [2 teste]; B₁ = [ 1 testa e 1 croce]; B₂ = [2 croci]

Questi sono degli eventi incompatibili ed esaustivi, ed è facile calcolare le probabilità condizionate dell'evento T = [esce testa] dato B₀, B₁ , oppure B₂. Se siamo in condizioni di completa incertezza, è naturale valutare gli eventi B_k equiprobabili. Si ricava dunque facilmente:

P(T) = P(B₀)P(T| B₀) + P(B₁)P(T| B₁) + P(B₂)P(T| B₂) = (1 + 0.5 + 0)/3 = 0.5

cioè lo stesso risultato che si otterrebbe per una moneta non truccata!

Si noti che, se si adotta l'interpretazione frequentista, nel caso di moneta non truccata il numero 0.5 rappresenta anche la frequenza relativa - su un gran numero di lanci - dell'evento "Testa". Invece, se la stessa moneta truccata viene lanciata più volte, la frequenza relativa dell'evento in questione è pari a 0, a 0.5, oppure a 1 a seconda del tipo di moneta. Il valore 0.5 rappresenta dunque in tal caso solo una "media pesata" di tali frequenze relative, che esprime - correttamente - il nostro "grado di fiducia", in relazione alle informazioni disponibili, rispetto al verificarsi dell'evento in questione. Questo è uno dei casi in cui l'interpretazione frequentista della probabilità cade in difetto. Se invece ad ogni lancio viene scelta una moneta tra le tre possibili ( di composizione B₀, B₁, oppure B₂ ) con uguale probabilità , la frequenza relativa sarà anche in questo caso, come è facile rendersi conto, pari a 0.5. L'interpretazione soggettiva, d'altro canto, rimane sempre valida.

Nota: quanto detto vale con riferimento ad un singolo lancio, senza conoscere i risultati dei lanci precedenti, nell'ipotesi che essi avvengano tutti con la stessa moneta. E' chiaro infatti che, se assistiamo al risultato di un lancio, esso ci darà informazioni sulla moneta: ad esempio, se esce croce al primo lancio - evento C₁ - escluderemo il caso B₀ , ossia porremo P(B₀|C₁)=0; in tal caso, è possibile dimostrare - sempre mediante la probabilità totale -che la probabilità dell'evento T nella prossima estrazione sarà pari a 1/6 (e se anche al secondo lancio esce croce, come valutereste la P(T) al 3° lancio?). In effetti, in tal caso, come si può dimostrare (lo si provi a fare per esercizio) i successivi lanci - anche se siamo in un meccanismo "con rimessa" (un discorso simile lo si può fare con un'urna con due palline, di composizione incognita, con estrazione con rimessa) - non sono più indipendenti, e questo dovrebbe essere chiaro interpretando la dipendenza come informazione (se non conosciamo la moneta, ogni lancio ci dà una certa informazione sulla moneta, e di conseguenza sui lanci successivi!).

Analogamente, con riferimento all'esempio del lotto, il fatto che la probabilità di estrazione non dipenda dal trucco, è vero solo se non si conoscono i risultati delle precedenti estrazioni, o non se ne tiene conto, o se il "trucco" varia di volta in volta in maniera incognita. Quindi, ad esempio, la probabilità di vittoria rimane inalterata solo per chi scelga i numeri a caso, magari anche in base ai sogni fatti o ad avvenimenti particolari, ma senza tener conto dei cosiddetti "ritardi".

D'altronde, se si gioca supponendo le estrazioni equiprobabili, il calcolo delle probabilità dovrebbe insegnare che non ha senso tener conto dei ritardi, perché ad ogni estrazione la situazione "riparte da zero", nel senso che ogni numero ha sempre probabilità pari ad 1/90 di essere estratto, indipendentemente dai risultati delle precedenti estrazioni (si dice anche che le estrazioni con rimessa costituiscono un meccanismo "senza memoria"), con buona pace delle "statistiche" sui ritardi riportate dai giornali, compilate da ( e per.. ) persone che non conoscono la probabilità

E' anche vero però che, per la "legge dei grandi numeri" - la quale può essere legittimamente invocata nel caso di estrazioni indipendenti - ogni dato numero deve uscire all'incirca 1 volta su 90, e dunque ritardi molto grandi rispetto a 90 sono poco probabili. Come conciliare questi due aspetti, apparentemente contrastanti, è un buon argomento di riflessione - peraltro non banale - che si lascia al lettore.

2.13 FORMULA DI BAYES

La formula di Bayes non è altro che un modo diverso di calcolare una "probabilità inversa", utilizzando la probabilità totale. Introduciamo tale formula con un esempio:

Esempio 1 Con riferimento all'Es. 6 del par. precedente ("moneta truccata"), si supponga che il risultato del lancio sia "croce"(evento "C"). Quale è la probabilità che la moneta sia di tipo B₀, B₁ oppure B₂?"

Bisogna valutare le P(B_k|C). Iniziamo, ad esempio, da B_1. Essendo nota la P(B₁) = 1/3, e la P(C|B₁) = 0.5, è naturale adoperare la relazione che fornisce la "probabilità inversa":

nella quale rimane da calcolare solo la P(C), il che - essendo note le P(C|B_k) - può essere fatto mediante la probabilità totale, come già visto nell'esempio in questione per il calcolo di P(T). Naturalmente, si ha P(C) = 0.5 (d'altronde, deve essere P(C) = 1 - P(T)). In definitiva:

P(B₁|C) = (1/3)(0.5/0.5) = 1/3 = P(B₁)

Dunque, B₁ e C sono indipendenti. Ma, naturalmente, come già detto, il risultato del lancio ci dà informazioni sulla moneta, infatti è chiaro - e risulta anche dal calcolo - che:

P(B₀|C) = 0; P(B₂|C) = 2/3

(Naturalmente, la somma delle probabilità P(B_k|C) deve essere pari ad 1!). Tali relazioni mostrano come le probabilità "a priori" (prima del lancio della moneta) P(B_k)- tutte pari ad 1/3 - si modifichino, dopo il lancio, nelle probabilità "a posteriori" P(B_k|C). Dopo il lancio, l'ipotesi più probabile è - naturalmente - quella che la moneta sia di tipo B₂ (con due teste). Altrettanto naturalmente, C non è indipendente da B₀ e B₂.

Per risolvere questo problema, abbiamo in effetti applicato la formula di Bayes, che ora si espone nel caso più generale. Essa, comunque, è una semplice riscrittura della probabilità condizionata, in cui si applica la probabilità totale.

Formula di Bayes

Nelle stesse ipotesi di validità del teorema della probabilità totale, vale la formula (a volte detta impropriamente "teorema") di Bayes:

A, B₁,.., B_n, IA W 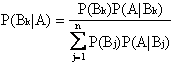Per k = 1, 2, , n (1)

purché le probabilità condizionate siano definite (ovvero tutte le probabilità degli eventi siano positive). Il teorema di Bayes permette di calcolare la probabilità di uno degli eventi (B_k|A) in funzione della probabilità dei singoli eventi B_k e delle probabilità condizionate P(A|B_k).

La dimostrazione è immediata, sulla base della relazione, già vista:

(2)

ed esprimendo poi la P(A) mediante la probabilità totale. Si noti che, correttamente, la somma delle k probabilità date dalla (1) è pari ad 1 (il denominatore è costante rispetto a k; infatti è pari a P(A)).

La formula di Bayes è interpretabile come segue: sia A un effetto noto, potenzialmente dipendente da un numero n di "cause" o ipotesi B_k; ogni causa può generare l'evento A secondo le probabilità note P(A|B_k). Le ipotesi, d'altronde, possono essere vere con probabilità " a priori" - cioè prima di osservare l'effetto - P(B_k) (si pensi appunto all'esempio della moneta). Il teorema di Bayes permette di rispondere alla seguente domanda: qual è la probabilità che, essendosi verificato A, sia vera l'ipotesi B_k ? Si può anche dire: "qual è la probabilità che A sia stato causato da B_k?". Ma ciò non è del tutto corretto, come si può dedurre dall'esempio che segue.

Le P(B_k|A) vengono definite probabilità a posteriori dell'ipotesi B_k noto l'effetto A e sono funzioni, mediante la (2) delle probabilità a priori P(B_k) che hanno le singole ipotesi di verificarsi e delle probabilità probative P(A|B_k) che l'effetto sia osservato essendo vera l'ipotesi k-sima (oppure, un po' impropriamente, che l'effetto "sia dovuto all'ipotesi k-sima").

Si osservi che, essendo il denominatore della (1) costante rispetto a P(B_k) - cioè esso è lo stesso per tutti gli eventi B_k - P(B_k|A) risulta proporzionale a P(A|B_k) P(B_k); cioè, la probabilità a posteriori sull'ipotesi B_k si modifica rispetto alla probabilità a priori sulla stessa ipotesi B_k grazie all'informazione P(A|B_k) relativa all'evento A.

La struttura logica del teorema di Bayes è proprio quella della ricerca scientifica moderna che da informazioni deducibili dall'esperienza (le probabilità probative) e da informazioni precedenti (le probabilità a priori), prende decisioni a favore di una certa ipotesi (paragonando le probabilità a posteriori). La formula di Bayes si appresta molto bene a descrivere il meccanismo dell'apprendimento, ed è per questo motivo molto utilzzata nell'ambito delle decisioni in condizioni di incertezza, ad esempio nella diagnostica (sia medica che industriale), nonché nell'intelligenza artificiale. Ad esempio, nel campo della diagnostica medica, il problema è quello di risalire da un certo sintomo A alla malattia B_k; normalmente, sono note le P(B_k) a priori (frequenza della malattia nella popolazione in esame), e le P(A|B_k), probabilità che il sintomo A sia causato dalla malattia B_k. Il medico dovrà valutare le probabilità " a posteriori" P(B_k|A), in modo da effettuare la diagnosi in base all'ipotesi "più probabile" sulla base dl sintomo. Del tutto analogo è il ragionamento nel caso della diagnostica industriale, come ad esempio si è visto nel passaggio dall'osservazione del guasto del sistema alle probabilità di guasto dei singoli componenti.

Esempio 2 Consideriamo ancora l'esempio 1 del par. precedente: consideriamo un intervallo di tempo passato in cui sappiamo essere valide le ipotesi di tale esempio. Supponiamo di sapere che, nell'intervallo di tempo in esame, la linea fosse guasta. Con che probabilità, in quell'intervallo, le condizioni atmosferiche erano avverse?

Sia G l'evento " linea guasta"; Conosciamo P(G|TF) = 1- P(S|TF) = 0.01 e P(G|TA) = 1- P(S|TA) = 0.18; vogliamo conoscere P(TA|G). Si ha semplicemente:

P(TA|G) = P(TA)P(G|TA)/P(G) = (0.02)(0.18)/P(G); la P(G) si può calcolare mediante il teorema della probabilità totale, come in effetti abbiamo già fatto nell'esempio 1, ottenendo: P(G) = 1 - P(S) = 1- 0.9866 = 0.0134. Dunque:

P(TA|G) = (0.02)(0.18)/(0.0134) = 0.269.

A seguito dell'evento "G", la probabilità a posteriori dell'evento "TA" risulta naturalmente molto maggiore di quello " a priori", P(TA) = 0.02.

Chiaramente, poi: P(TF|G) = 1- P(TA|G) = 1 - 0.269 = 0.731.

Nota: Si noti che la differenza tra tali i valori di P(TF|G) e P(TA|G) è legata al fatto che P(TF) è molto maggiore di P(TA), e non vuol dire, naturalmente, che è poco probabile che il guasto fosse causato da condizioni avverse.

Esempio 3 (Teorema dell'estrazione - 2a parte)

Riprendiamo l'Es. 3 del par. precedente, e supponiamo ora che alla seconda estrazione la pallina estratta sia bianca, senza conoscere l'esito della prima estrazione; ci chiediamo, quale è la probabilità che anche la prima estratta fosse bianca?

Si vuole dunque conoscere la probabilità P(B₁|B₂): poichè conosciamo la probabilità condizionata "inversa", dalla relazione: P(B|A) = P(B)P(A|B)/P(A) ricaviamo: P(B₁|B₂) = P(B₁)P(B₂|B₁)/P(B₂); poiché: P(B₁) = P(B₂), come abbiamo appunto visto con la probabilità totale, si ha semplicemente:

P(B₂|B₁) = P(B₁|B₂) = (b-l)/(N-l).

Qui abbiamo un altro esempio in cui il calcolo della probabilità condizionata di A all'evento B non presuppone che l'evento B si verifichi prima di A, come già detto. Anche stavolta il risultato appare, a ben vedere, intuitivo.

2.14 INDIPENDENZA CONDIZIONALE.

Due eventi A e B si dicono condizionalmente indipendenti, dato l'evento C se:

P(A B|C) = P(A|C)P(B|C)

Se è vera la (1), si può dimostrare che valgono le seguenti relazioni:

P(A|(B C)) = P(A|C) e P(B|(A C)) = P(B|C)

In generale due eventi condizionalmente indipendenti non sono necessariamente indipendenti.

Esempio Si considerino due linee elettriche, a e b, per le quali valgano le stesse ipotesi di cui all'esempio 1 del par. 2.12.1; si supponga che gli eventi di funzionamento (A e B) delle due linee siano condizionalmente indipendenti, data la conoscenza delle condizioni atmosferiche (ovvero gli eventi: TF e TA). Si verifichi che però tali eventi non sono indipendenti.

Questo esempio illustra come l'incertezza delle condizioni ambientali possa implicare la dipendenza statistica tra eventi altrimenti ritenuti indipendenti; ciò ha un significati intuitivo: provate a discuterlo (Suggerimento: il ragionamento è analogo a quello fatto a proposito della moneta incognita).