 |  |
| |
 |
tecnica |
|
PROPRIETA' DELLA TRASFORMATA DI FOURIER
ADDITIVITA': x(t)=a1x1(t)+ . +anxn(t) T X(f)=a1X1(f)+ . +anXn(f)
x(t) reale T X(f)=X*(-f)
x(t) reale e PARI
X(f) REALE (e pari)
x(t) reale e DISPARI
X(f) IMMAGINARIA (e pari)
PRINCIPIO DI DUALITA': F[X(t)]=x(-f)
CONIUGAZIONE: F[x*(t)]=X*(-f)
AREA SOTTESA DA x(t): x(t)dt=X(0)
TRASLAZIONE NEL TEMPO: z(t)=x(t-t0) T
Z(f)=
TRASLAZIONE IN FREQUENZA: Z(f)=X(f-f0) T
z(t)=
CAMBIAMENTO DI SCALA: z(t)=x(kt) (k>1 compressione, k<1 espansione) T Z(f)=
DERIVAZIONE: Se 
T
B(f)=j2pfA(f)
INTEGRAZIONE Se b(t)=
T
B(f)=
PROPRIETA' DELLA CONVOLUZIONE
x(t) y(t)= y(t) x(t)
Se x(t) dura tx e y(t) dura ty la convoluzione durerà tx+ty
Se x(t) y(t)=a(t) allora x(t-t0) y(t)=a(t-t0) e x(t-t1) y(t-t2)=a(t-t1-t2)
x(t)*d(t)=x(t)
FORMULE UTILI
serie di fourier x(t)=axkej2pk/Tt con 
convoluzione x(t) y(t)=
correlazione per segn.di
energia Ryx(t)= 
=
=x(t y t
correlazione per segn.di
potenza Ryx(t)=
=
densità
spettrale di potenza per segn.periodici x(t)=
: Dx(f)=
filtro
passa-basso rc 
con 
e 
; h(t)=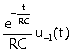
varianza di una somma var(x h)=var(x)+var(h)+2cov(x h con cov(x h)=E[xh E[x]E[h]=m11 mxmy
ovvero: sx+y sx sy +2cov(x h
funz.
caratteristiche: Gaussiana Cx(u)=
, Cauchy Cx(u)=e-a|u|
TIPS & TRICKS
La potenza di Acos(2pf0t+j) è P=A2/2.
Potenza ed energia sono invarianti per traslazione.
I coeff. xk della serie di Fourier si possono calcolare anche con la trasf. G(f) della f.elementare g(t).
Quando l'ingersso di un sistema è una funzione periodica, è conveniente svilupparla secondo Fourier e poi calcolarsi lo spettro, che sarà un treno di impulsi.
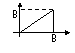
T 
L'autocorrelazione è invariante per traslazioni quindi autocorrelaz.di Asen(2pf0t+q)=autocorrelaz.di Asen(2pf0t)
La mutua correlaz.invece, è invariante per traslaz.solo se x(t) e y(t) traslano dello stesso valore.
L'autocorrelazione inoltre è periodica dello stesso periodo della funzione correlante.
Risposta ad un segnale armonico Aej2pf0t: A|H(f0)|ejF(f0)ej2pf0t
Risposta ad un segnale Acos(2pf0t+j): A H(f0) cos[2pf0+j jH(f0)] (sistema lineare)
Tieni presente che rectD(t-t0)=u-l[t (t0-D u-l[t (t0+D
Se
in un sistema lineare x(t) y(t)
allora 
Quando la relazione che lega y(t) a x(t) è di tipo differenziale, conviene operare nel dominio della frequenza.
d (t)=,poiché d(t)x(t)=d(t)x(0),=d(t)d(0) ovvero un'impulso di area
Ricordati di raddoppiare X+(f) quando calcoli Zx(f)
Per
calcolare le componenti analogiche di bassa frequenza si può vedere se 
è facilmente
scomponibile nelle parti pari e dispari.
h(t)=e-atu-l(t) T jhh t)=A0e-a t con A0=1/2a
Sia nella convoluzione che nella correlazione la y(t-t) si sposta da sinistra a destra per le t (o t) crescenti.
xs e xc si ottengono da x(t) moltiplicando per sen(2pf0t) e cos(2pf0t) e poi facendoli passare in un passa-basso.
Media e varianza di alcune densità si possono calcolare tramite la funzione caratteristica.
Per calcolare E[h] conoscendo E[h x] si ha che E[h]=Ex[E[h x]] (attento al significato di quest'ultimo termine).
Per risolvere alcuni integrali, specialmente quelli con le gaussiane in mezzo, a volte bisogna mettere in evidenza l'integrale di una densità di probabilità, in modo tale da poterlo poi porre a 1 (anche se mx è complesso), oppure a volte si può mettere in evidenza anche un momento (es.s ) (vedi .3.3).
w x h
gaussiane indipendenti è ancora gaussiana (si può vedere tramite la
f.caratteristica) con mw=mx+my
e 
.
Quadratore:
fh(y)=
Una Raileigh in un quadratore h x dà in uscita una esponenziale.
Una gaussiana in un quadratore non dà niente di noto.
w=
gaussiane con m=0 e sx sy
è una Raileigh 
Se una fxh(x,y) è separabile in un prodotto f1(x) f2(y) allora x e h sono indipendenti.
Se X e Y sono indipendenti
E[XY]=E[X]E[Y] (attenzione E[X X]=E[X] E[X]
non vale!).
Variabili bidimensionali: fx h(w)= fxh(x,w-x)dx
Composizioni di 2 variabili aleatorie e variabili bidimensionali possono essere risolte graficamente.
Nelle
composizioni di variabili aleatorie h=g(x)
secondo una y=g(x), si può usare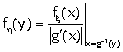 
sui rami e poi al limite sommare se i rami corrispondono a
uguali valori di y. (vedi esercizio .9 sugli appunti)
Z=X2+Y2
gaussiane con m=0 e s
è esponenziale 
Variabili che assumono solo valori positivi si possono spostare dentro o fuori i moduli (es. A|cos(t)|=|Acos(t)| )
Ricordati che Cxx(0)=s e Rxx(0)=E[X2(t)]=m2=m11.
Cxx(0) e Rxx(0) si possono calcolare dagli integrali da - a + delle loro F-trasformate.
Ricorda che la correlazione per i processi è la media E[X(t)X*(t-t
La correlazione E[Y(t)Y*(t-t)] può essere calcolata in funzione di X(t) conoscendo E[X(t)X*(t-t
Anche ai processi si può applicare la linearità di E considerando le parti legate a t come delle costanti.
Nelle correlazioni ricordati il coniugato! E[XX*].
Essendo Rxx(t)=Cxx(t)+mx2, la sua trasformata Sxx(f) avrà in 0 un impulso di ampiezza mx2 a meno che mx=0.
L'autocorrelazione (e la covarianza) di un processo armonico è Rxx(t)=Cxx(t)=(1/2)E[A2]cos(2pf0t
Onda
p.a.m. stazionaria con simboli SSL ha mX=
, Rxx(t)=
.
L'autocorrelazione all'uscita di un quadratore Ryy(t1,t2)=E[X2(t1)X2(t2)]=E[X1X2X3X4], poiché per x x x x gaussiane si ha E[x x x x ]=R12R34+R13R24+R14R23, allora per un processo gaussiano X, vale Rxx(t1,t1)Rxx(t2,t2)+ +2Rxx(t1,t2)Rxx(t1,t2) e se il processo è SSL vale Rxx2(0)+2Rxx2(t
L' autocorrelazione di un segn.armonico Acos(2pf0t+j) è Rxx(t)=A2/2cos(2pf0t).
Spesso ci sono delle onde p.a.m.camuffate (attento alla g(t-kT-q
Se X(t) è SSS, X(t) e X(t-t0) hanno la stessa fx(x) (non dipende da t).
R
di un processo derivato è Ryy=
.
Un segnale fatto di rect si può scomporre in rect che passa in un sistema con h(t) fatto di impulsi.
Tenere presente tutti i teoremi di Parseval.
ae-j2pkTf=Fad(f-kF) con F=1/T.
Tieni
presente che F-l
=j2ptx(t).
Nelle integrazioni con u-l(t) attenzione a metterlo anche dopo (sulla f.integrata).
Sen(2pf0t+j)
e cos(2pf0t+j)
sono ortogonali (infatti 
)
Anche cos(2pf1t) e cos(2pf2t) sono ortogonali.
Quando un processo gaussiano entra in un sistema, quasi sempre ne esce un altro gaussiano.
19 1.31
|
Privacy
|
© ePerTutti.com : tutti i diritti riservati
:::::
Condizioni Generali - Invia - Contatta
