 |  |
| |
 |
tecnologia meccanica |
|
Obbiettivi Verificare il comportamento reale del derivatore e dell'integratore di Miller
 |
CENNI TEORICI
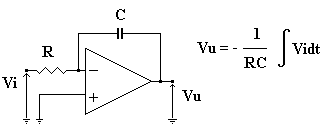
INTEGRATORE
L'uscita risulta sfasata in anticipo di 90 indipendentemente dalla pulsazione, assumendo ampiezze tanto più grandi quanto più piccolo è il valore della pulsazione stessa. Al limite, in continua, l'amplificazione tende a infinito; ciò è facilmente comprensibile, dal momento che in queste condizioni il condensatore si comporta come circuito aperto e quindi l'operazionale lavora come retroazione.
Il comportamento del circuito è quindi critico in continua, ed in generale a frequenze molto basse. In particolare, occorre considerare l'effetto della tensione di offset e delle correnti di polarizzazione; anche scegliendo operazionali con ridotti valori per questi due parametri, l'integrazione di una pur minima componente continua in ingresso porta inevitabilmente nel tempo l'uscita in saturazione. Nei sistemi che utilizzano l'integratore come vero e proprio operatore matematico, occorre quindi un qualche sistema per scaricare periodicamente il condensatore.
Particolare cura dev'essere impiegata nella scelta del condensatore. Occorre infatti utilizzare un componente dotato di ridotta corrente di fuga.
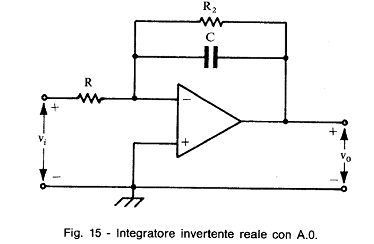
Per ottenere prestazioni costanti al variare della temperatura è inoltre indispensabile sciegliere condensatori a ridotto coefficiente termico. Per rendere l'integratore meno stabile all'influenza delle componenti continue si può utilizzare il seguente circuito.
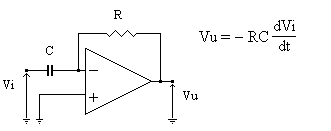
DERIVATORE
L'uscita è in ritardo di fase di 90° rispetto all'ingresso ed assume ampiezze tanto maggiori quanto più grande è la pulsazione. Questo è comunque vero solo nell'intervallo di frequenze in cui l'operazionale mantiene costante la sua amplificazione; in ogni caso il circuito ha comportamento critico alle alte frequenze ed innesca oscillazioni a causa dell'elevata amplificazione delle correnti di rumore.
DESCRIZIONE DELL'ESPERIENZA
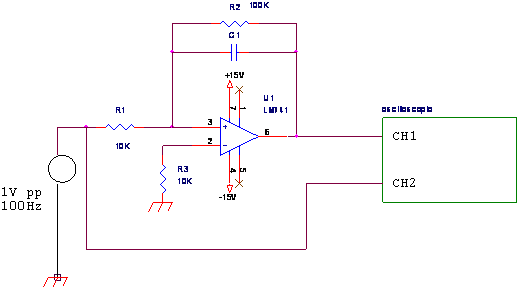
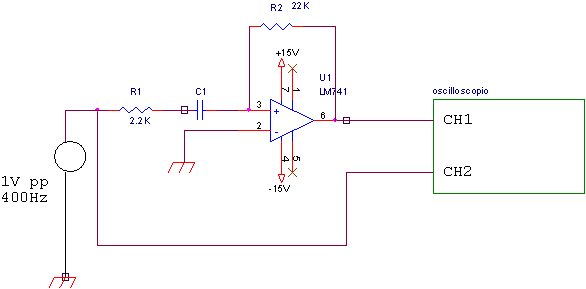
Si assembli il circuito seguendo lo schema di ura relativo al derivatore, prestando attenzione che i piedini dei vari componenti e i fili conduttori siano saldamente a contatto con i canali della bread board. Collegare alla bread board l'alimentatore stabilizzato in modo da fornire una d.d.p pari a 30V (+-l5V). Si collega un generatore di funzioni al circuito fornendo così un segnale triangolare di un Vpp di frequenza variabile (una prova a 400, una ad 1K e una a 30KHz). . Si procede poi alla verifica della prima parte dell'esperienza congiungendo al circuito ottenuto un oscilloscopio e visualizzando i risultati
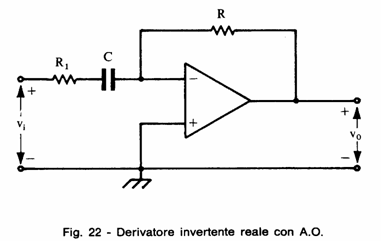
Nella seconda parte si modifica il circuito in modo da realizzare l'integratore di Miller, le fasi seguenti sono uguali a quelle precedentemente descritte, con la differenza che questa volta si dovrà fornire un segnale ad onda quadra di ampiezza pari ad 1Vpp. Le tre prove andranno eseguite a 10K, 4K, e 100Hz
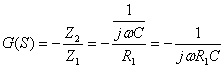
INTEGRATORE DI
MILLER IDEALE: Il circuito è nella classica conurazione invertente pertanto
in regime sinusoidale con s = Jw si avrà
INTEGRATORE DI MILLER REALE: Applichiamo ancora il metodo della trasformata di Laplace e otteniamo
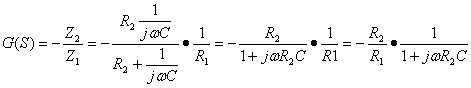
è la pulsazione di taglio superiore della rete (
è la frequenza di taglio superiore)
Avremo allora che per w<<wts FDT 
per cui la rete tende a comportarsi come amplificatore
invertente
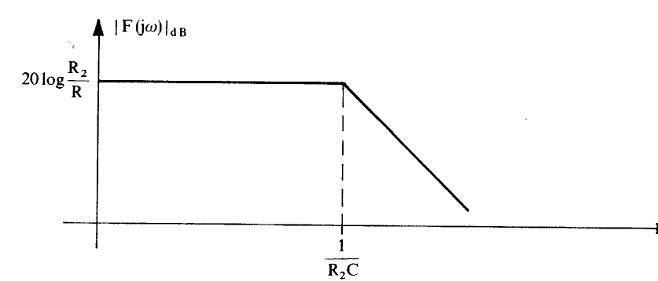
Per w>>wts FDT 
la funzione di trasferimento coincide con quella dell'integratore
di Miller ideale, e la rete tende a comportarsi da integratore.
La presenza del carico resistivo non modifica praticamente il comportamento della rete, a causa della piccola impedenza di uscita della rete stessa
Il diagramma di Bode del modulo della funzione di trasferimento è il seguente
Derivatore DI MILLER IDEALE: Il circuito è nella classica conurazione invertente pertanto in regime sinusoidale con s = Jw si avrà
DERIVATORE DI MILLER IDEALE
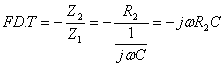
DERIVATORE DI MILLER REALE
è la pulsazione di taglio inferiore della rete;
Avremo allora che per w>>wti FDT per cui la rete tende a comportarsi come amplificatore
invertente
Avremo allora che per w<<wti FDT 
la funzione di trasferimento coincide con quella del derivatore
di Miller ideale e la rete tende a comportarsi come derivatore
La presenza del carico resistivo non modifica praticamente il comportamento della rete, a causa della piccola impedenza di uscita della rete stessa
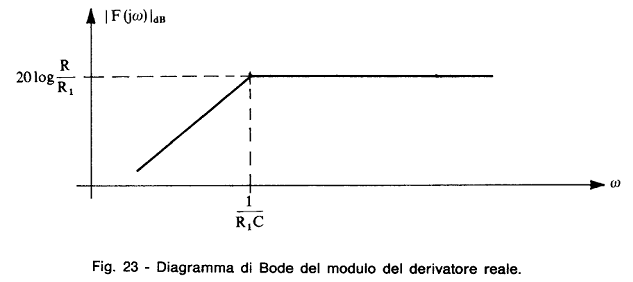
INTEGRATORE DERIVATORE
Frequenza di teglio= 15,4KHz Frequenza di taglio =723.8Hz
V opp a 10KHz VIPP T dove T = 1 = 1.136 V opp a 400Hz 4RC VIPP dove T = 1 = 0.165
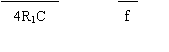
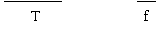
V opp a 4KHz = VIPP T dove T = 1 = 2.184 V opp a 1KHz 4RC VIPP dove T = 1 = 0.436
V oppTeorico
a 100Hz = -RS Vi = 100/10 = 10 V oppTeorico a 30KHz = -RS Vi =
100/10 = 10
|
Frequenza d'ingresso [Hz] |
VOPP rilevato |
VOPP teprico |
|
|
|
|
|
1K |
|
|
|
30K |
|
|
INTEGRATORE
|
Frequenza d'ingresso [Hz] |
VOPP rilevato |
VOPP teprico |
|
10K |
|
|
|
4K |
|
|
|
|
|
|
OSSERVAZIONI SUI VALORI MISURATI
INTEGRATORE : A 100 Hz cioè per f molto minore della ft la rete non integra affatto e si comporta come amplificatore invertente, con guadagno (R2/R1) 10
A 4 KHz la rete comincia a perdere le caratteristiche di amplificatore invertente e la rete integra abbastanza correttamente: lo sfasamento è di circa 45° il guadagno diminuisce ed inizia a vedersi un certo sfasamento. La non è ancora un'onda triangolare ma si presenta come una sucessione di curve esponenziali
A 10 KHz la rete integra bene; lo sfasamento è di 90°. L'uscita è una sucessione di rampe
A 1KHz la rete deriva con una certa approssimazione; la risposta anche se di tipo quadro presentava tempi di commutazione ancora molto lunghi
A 30 KHz la rete non deriva affatto ma si comporta come amplificatore invertente
Confrontando i dati rilevati con quelli teorici possiamo notare il buon esito dell'esperienza
|
Privacy
|
© ePerTutti.com : tutti i diritti riservati
:::::
Condizioni Generali - Invia - Contatta
