Ferraresi Gilles     III A

RELAZIONE DI T.D.P

Le resistenze nei circuiti elettrici-

Scopo: Verificare dal punto di vista pratico la teoria riguardante i resistori

MATERIALI E STRUMENTI REALIZZATI

Basetta da laboratorio

Multimetro digitale

Alimentatore stabilizzato

Fili conduttori

Resistenze serie E12

CENNI TEORICI

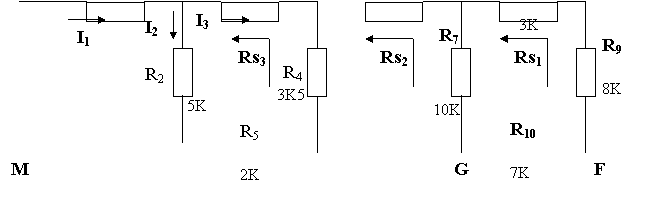
I resistori sono dispositivi che hanno la proprietà di opporsi alla circolazione della corrente elettrica e di degradare in calore l'energia elettrica assorbita. Il loro comportamento elettrico in corrente continua soddisfa la legge di OHM: R=V/I. Nel S.I l'unità di misura della resistenza è l'ohm. L'ohm è la resistenza di un conduttore attraversato dalla corrente di 1 ampere quando ai suoi estremi è applicata la differenza di potenziale di un volt. La resistenza che un conduttore offre al passaggio di corrente dipende dalla natura del materiale di cui è costituito, dalle sue caratteristiche geometriche e dalle condizioni di temperatura. Per un dato valore di temperatura, essa è proporzionale alla lunghezza e inversamente proporzionale alla sezione. Con poche eccezioni, aumenta all'aumentare della temperatura.

In un circuito elettrico possono essere inserite una o più resistenze disposte in serie o in parallelo. Due o più resistenze sono disposte in serie quando sono attraversate dalla stessa intensità di corrente. Sperimentalmente si calcola che la resistenza totale di due o più resistenze disposte in serie è uguale alla somma delle singole resistenze.

Due o più resistenze sono disposte in parallelo quando sono condotte fra punti che hanno lo stesso potenziale. Sperimentalmente si calcola che la resistenza totale di due o più resistenze disposte in parallelo è uguale al reciproco della somma dei reciproci delle singole resistenze.

Quando la corrente raggiunge un nodo si divide in tanti flussi di corrente quante sono le resistenze. Per calcolare queste correnti è utile usare il  primo principio di Kirchhoff che consiste nell'effettuare la somma algebrica delle correnti che confluiscono in un nodo eguagliandole a zero.

Ferraresi Gilles 3^A

SINTESI OPERATIVA

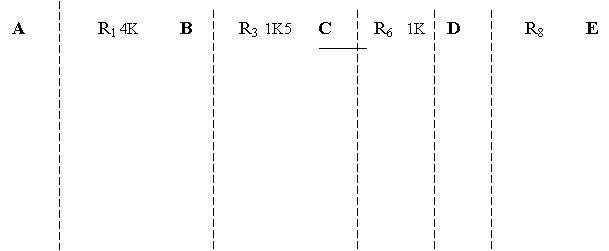
Dopo aver assemblato il circuito, seguendo lo schema elettrico sopra illustrato, si procede nell'esecuzione dell'esperienza. Per quanto riguarda la realizzazione del circuito su basetta, occorre prestare molta attenzione alla sua realizzazione, in quanto si potrebbe incorrere in errori, a volte molto banali, che potrebbero compromettere la buona esecuzione dell'esperienza. Inoltre, abbiamo visto come, quando il circuito risulta essere molto complesso, come in questo caso, sia utile realizzare circuiti più semplici, in modo da riuscire a risalire più facilmente alle varie resistenze equivalenti, rendendole più chiare.

Innanzitutto occorre scegliere il valore di resistenza che più si avvicina a quello richiesto; utilizzando la serie E12 la quale ha un valore nominale che varia in più o in meno del 10%, come nel nostro caso. Per avere una misura più accurata, si procede nel misurare la resistenza col multimetro e si prende nota del valore effettivo della resistenza. Si calcola lo scarto fra i due valori.

Dopodiché, dal punto di vista teorico, si effettuano vari calcoli per ricondursi alla resistenza equivalente, tenendo conto della disposizione delle varie resistenze (serie, parallelo). Una volta effettuati i vari calcoli, si procede a calcolare sperimentalmente i valori delle varie R_eq. Anche in questo caso si confrontano i due valori, e se ne verifica in questo modo l'attendibilità dei risultati.

Per quanto riguarda le tensioni nelle varie maglie, ci limitiamo a calcolarle sperimentalmente, in quanto non possediamo le conoscenze per calcolarle utilizzando relazioni matematiche. Riusciamo invece a calcolare i valori delle correnti incognite facendo uso anche del primo principio di Kirkoff, e a confrontarli con i valori letti dal multimetro. Con questa ultima operazione si conclude l'esperienza e si analizzano i vari dati ottenuti.

Tabelle, calcoli

Con questa tabella, risulta molto evidente, il discorso riguardante le serie commerciali delle resistenze, e soprattutto balza subito agli occhi, come esista una certa tolleranza di fabbricazione che si discosta dal valore nominale. Per questo tipo di esperienza non erano, comunque necessarie resistenze di precisione. La conoscenza di questi valori normalizzati, come detto in precedenza è importante in quanto, dopo aver ricavato i valori delle resistenze del circuito che si sta dimensionando, occorre ricercare fra i vari valori della serie prescelta quello che approssima meglio il valore del valore calcolato

x 100

Scarto percentuale = Valore misurato - valore nominale

Valore nominale

Scarto percentuale su R1= 0,5%

Scarto percentuale su R2= -l,1%

Scarto percentuale su R₃= -0,7%

Scarto percentuale su R₄= -0,9%

Scarto percentuale su R₅= 1,1%

Scarto percentuale su R₆= -l%

Scarto percentuale su R₇= -l,1%

Scarto percentuale su R₈= -0,4%

Scarto percentuale su R₉= 1,4%

Scarto percentuale su R₁₀= -l,7%

Ferraresi Gilles 3^A

R8910= R8+R9+R10 =2,69+8,32+6,68= 17,69KW RD1 R78910 =    R8910 x R7 R8910 + R7 R6 Ra RA6= RA + R6= 6,34+0,99= 7,33K= RD2 R4 G RA64 = RA6 x R4 R3 RA64   VALORI  EFFETIVI

RD4= 6,42K

=6,34 KW= RA   RD3= 5,56K

RD2= 7,33K

C   RD1= 17,70K

RS1= 2,31K

RS2= 2,04K

RS3= 2,11K

VALORI CALCOLATI

RD4= 6,41K

= 2,26K   RD3= 5,57K

RD2= 7,33K

B   RA6 // R4   RD1= 17,69K

RS1= 2,31K

RS2= 2,03K

RS3= 2,11K

	Confronto fra valori effettivi e calcolati delle varie Req

R3A645=  R3+RA64+R5= 5,57 KW = RB=  RD3

R₅

M

A B

R₁

R₂ R_B2= R₂ x R_B =2,53 KW

R_B R₂ x R_B

M

A    R1

R_2B Req= R1+R_2B= 3,88+ 2,53= 6,41 KW

Calcolo delle correnti UAM Req Va-(R1 x I1) R2 Primo principio di Kirchhoff nel nodo B I1-l2= I3   I3 1,56 - 0,86= 0,7 mA

M

2,11 KW