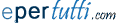Struttura atomica ed effetto Zeeman

Struttura atomica ed effetto Zeeman

• La descrizione della struttura atomica non può avvenire nell'ambito della meccanica classica, e necessita dell'uso della meccanica quantistica.
• Fra le principali particolarità associate alla natura quantistica dei sistemi atomici, emerge il fatto che gli atomi esistono in stati stazionari la cui energia non assume qualunque valore si voglia, ma solo dei valori predeterminati.
• L'insieme di tali valori dipende dalla specie atomica considerata.
• Un atomo può transire da uno stato all'altro cedendo o acquistando energia dalla radiazione elettromagnetica.
• I diversi livelli atomici possono essere caratterizzati da particolari numeri (numeri quantici) taluni dei quali sono interi (1,2,3 . ; -2, -l, 0, 1, . ), altri semi-interi (-3/2, -l/2, +1/2, . ). I numeri quantici caratterizzano compiutamente gli stati stazionari, essendo associati a grandezze fisiche che sono assegnate in quegli stati, come l'energia, il momento angolare ecc.
• Nelle transizioni, i numeri quantici possono subire solo dei cambiamenti predeterminati, ad esempio di una sola unità. La meccanica quantistica fornisce le limitazioni esistenti per queste transizioni, queste limitazioni sono note come 'regole di selezione'.
• Come diretta conseguenza, le possibili transizioni atomiche (soddisfacenti le regole di selezione) sono in numero assai inferiore al numero di coppie che sarebbe possibile scegliere nell'insieme dei livelli energetici esistenti.
• Nella ura 1a sono rappresentati (non in scala) i livelli energetici di un metallo alcalino, corrispondenti ad alcuni valori dei numeri quantici.
• Ciascun livello, che è caratterizzato fra l'altro dal numero quantico J (momento angolare elettronico totale, composizione del momento angolare orbitale L e del momento di spin elettronico S), nasconde dei sottolivelli 'degeneri', cioè aventi lo stesso valore di energia, caratterizzati da un numero quantico J_z che può variare da -J a +J a salti di un'unità. Così uno stato con J=3/2, nasconde quattro stati con J_z=-3/2, J_z=-l/2, J_z=+1/2 e J_z=+3/2.

• Se si applica un campo magnetico, l'energia degli stati aventi differenti valori di J_z viene modificata differentemente a seconda del valore di J_z, come è rappresentato in . 1b per i soli livelli inerenti la transizione D₂.
• Solo alcune delle differenti coppie di sottolivelli sono connesse, e le relative transizioni devono essere associate all'assorbimento di fotoni di un'assegnata polarizzazione, indicata in ura 1b con sigma+ e sigma- per le polarizzazioni circolari destra e sinistra e con pigreco per la polarizzazione lineare.
• Quindi, ad esempio, facendo interagire un vapore atomico immerso in campo magnetico con radiazione elettromagnetica polarizzata circolarmente sigma+, si osserva che la riga spettrale associata alla transizione D₂ si scompone in due componenti, associate alle transizioni J_z=-l/2 --> J_z=+1/2 e J_z=+1/2 --> J_z=+3/2.
• Per approfondimenti sull'effetto Zeeman (e non solo), esiste un bel sito web (in inglese), che consigliamo di visitare. ½ sono descritti vari esperimenti di fisica moderna attuabili in laboratori didattici.
• In realtà la struttura dei livelli del sodio è più complessa di quella appena descritta. Infatti, per bassi valori del campo magnetico, quali quelli utilizzati in una trappola magneto-ottica, prima di considerare l'effetto del campo magnetico sui livelli di assegnato valore di J, occorre considerare che tali livelli possiedono una struttura, nota come struttura iperfine, dovuta all'interazione fra il momento magnetico associato al momento angolare totale J ed il momento associato allo spin nucleare I.
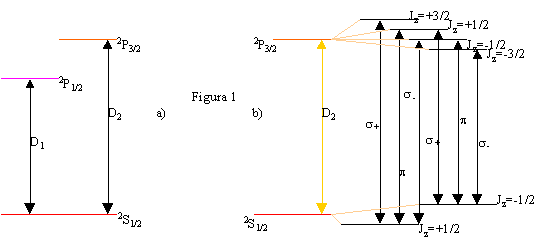
• La trattazione della struttura iperfine secondo i metodi della meccanica quantistica, permette di affrontare il problema con l'introduzione di un nuovo numero quantico F, associato alla somma di J e I. Già in assenza di campo magnetico, una dettagliata analisi spettroscopica della transizione D₂, mette in evidenza una struttura di livelli come quella rappresentata (non in scala) in ura 2.

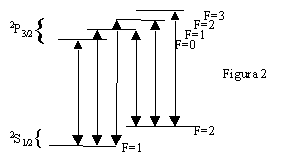
• Se consideriamo la sola transizione dal fondamentale ²S_1/2, F=1 (per la quale si può avere F_z=-l, 0, 1) all'eccitato ²P_3/2 F=0 (F_z=0), questa si separa per effetto del campo magnetico in tre righe spettrali, che corrispondono ad emissione o assorbimento di fotoni sigma+, pigreco o sigma-. Se il campo magnetico varia con la posizione, come avviene intorno al centro di una MOT, le tre transizioni avvengono a frequenze il cui spostamento dipende dalla posizione, come schematizzato (in scala enormemente esagerata) in ura 3.

• A causa dello spostamento di livelli che abbiamo descritto, l'assorbimento di un fotone con polarizzazione sigma+, se al centro, dove il campo magnetico è nullo, è possibile per atomi che hanno una certa (piccola) velocità verso la sorgente di luce, nella zona a sinistra del centro avviene per atomi che sono fermi o si spostano a destra, mentre a destra avviene per atomi che si spostano a sinistra.
• Identiche considerazioni, con una adeguata ri-definizione dei versi di polarizzazione, vanno fatte per gli altri fasci, che si proano in direzioni e versi differenti.
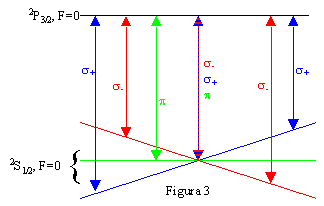
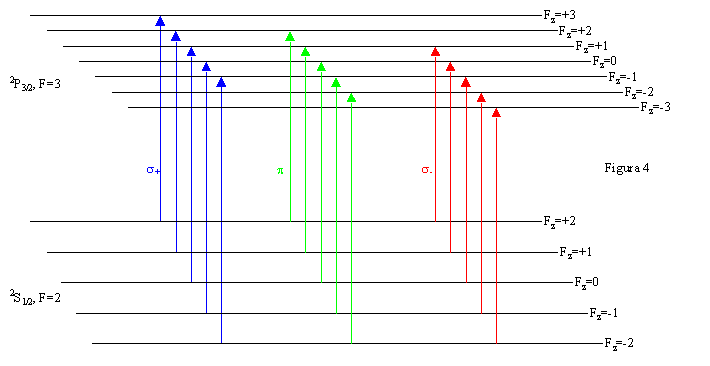
• Un discorso analogo si potrebbe fare per transizioni fra stati con differenti valori di F. Al crescere di F, il numero di sottolivelli Zeeman coinvolti cresce notevolmente. A titolo d'esempio, si consideri la transizione dal ²S_1/2, F=2 a ²P_3/2 F=3. La situazione per un campo B assegnato è rappresentata in ura 4, dove sono indicate le transizioni indotte da fotoni di diverse polarizzazioni.