CONTROLLI AUTOMATICI

Tesina:

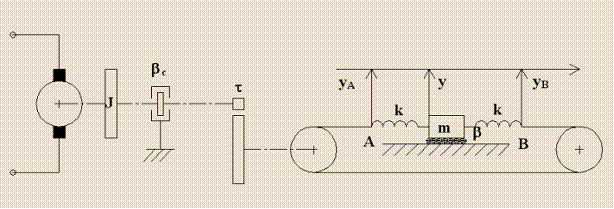
Controllo di un nastro trasportatore

Prof.: Fiorio Giovanni

Sommario:

Fotocopia del problema in esame

Costruzione del modello matematico 2 1.1 Equazioni sistema meccanico . . . . . . . . . . . . . . . . . . . 2

Determinazione G(s) metodo algebra dei blocchi 3

Risposta del sistema agli ingressi tipici 5 2.1 Ingresso a gradino unitario . . . . . . . . . . . .. . . . . . . . . 5 2.2 Diagrammi di Bode della G(s) . . . . . . . . . . . . . . . . . 8

Studio della condizione di stabilità assoluta 9

3.1 Criterio di Routh . . . . . . . . . . . . . . . . . . . . . . . . 9 3.2 Criterio di Nyquist . . . . . . . . . . . . . . . . . . . . . . . . 11 3.3 Criterio del luogo delle radici (LDR) . . . . . . . . . . . . . .. . 13

Valutazione della buona stabilità relativa . . . . . . . . . .. . . . . . . 16

4.1 Margine di fase . . . . . . . . . . . .. . . . . . . . . . . . . . 16

4.2 Margine di guadagno . . . . . . . . . . . .. . . . . . . .. . . . . 17

4.3 Limitazione picchi di risonanza . . . . . . . . . . .. . . . . . . . 18

Progetto a livello superiore . . . . . . . . . . . . . . . . . . . . . .. 22

Compensazione in cascata 22

Compensazione in retroazione 23

Altri tipi di strutturre 24

Progetto a livello intermedio e livello inferiore 25

6.1 Approccio mediante sintesi diretta . . . . . . . . . . . . . . . . . . 26

6.2 Approccio mediante "tentativo e verifica" . . . . . .. . . . . . . . . 31

7. Progetto del compensatore analogico 33

Verifica del compensatore analogico 39

8.1 1S Verifica: Analisi della W_r,c(s) . . . . . . . . . . . . . . . . . . 39

8.2 2S Verifica: Analisi della risp. al gradino con parametri di G(s) modificati 40

8.3 3S Verifica: Analisi della P(s) . . . . . . . . . . . . . . . . . .. . 41

9. Realizzazione del controllo digitale . . . . . . . . . . . . . . . . . . . 42

9.1 Progetto del compensatore analogico . . . . . . . . . . . . . . . . . 43 9.2 Inserimento del dispositivo di tenuta . . . . . . . . . . . . . .. . . . .. 47 9.3 Determinazione della C(z) . . . . . . . . . . . . . . . . . . . . .. . . 51

9.4 Prove di validazione . . . . . . . . . . . . . . . . . . . . . . . . 55

9.5 Conclusioni . . . . . . . . . . . . . . . . . . . . . . . . . . 61

1. Costruzione del Modello Matematico

Per la costruzione del modello matematico che caratterizza il sistema da controllare, sono state considerate le equazioni a livello meccanico. Partendo da esse, si è costruito il relativo schema a blocchi. Si è poi verificata l'esattezza dei calcoli con il metodo delle variabili di stato.

Per semplicità si è supposto che le condizioni iniziali fossero nulle (in quanto complicherebbe il lavoro senza risultati interessanti). In particolare si è posto che y_c sia il punto medio tra y_a e y_b, cioè y_c = (y_a - y_b)/2, al fine di evitare una costante aggiuntiva che infastidisce lo studio del sistema.

Il sistema considerato è ibrido, costituito cioè da parti meccaniche ed elettriche. La parte di comando è costituita da un motore in corrente continua che aziona il sistema meccanico di posizionamento della massa. Nel trattare questo sistema è opportuno separare le due parti, trattando indipendentemente la parte meccanica da quella elettrica.

Una volta scritte le equazioni, si passa alle L-trasformate, individuando una funzione di trasferimento che mi lega il comando del sistema V_a (tensione di armatura del motore) con l'uscita y (posizione istantanea della massa).

Equazioni del sistema meccanico

Divido quindi il mio sistema in vari sottosistemi, abinando ad ognuno di essi delle equazioni caratteristiche.

Motore elettrico:

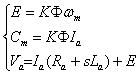Albero motore:

Massa:

cioè:   

Massa - molle:

Da queste ultime due si ottiene :

Determinazione G(s) (metodo algebra dei blocchi)

Posso quindi scrivere l'equazione finale che lega direttamente l'ingresso V_a con l'uscita y :

La funzione di trasferimento assume la forma:

dove:

Numericamente:

Ed infine si ha nella sua forma esatta:

anche scritta in forma abbreviata come:

Quindi scritta in questa forma, le costanti del polinomio a denominatore valgono:

a₀ = 1,04166666666666666666666666666667^.10^-6

a₁ = 1,47916666666666666666666666666667^.10^-4

a₂ = 0,115830664814814814814814814814815

a₃ = 2,16594043981481481481481481481481

a₄ = 266,771302083333333333333333333333

a₅ = 0

2. Risposta del sistema agli ingressi tipici

Conoscendo la funzione di trasferimento del sistema, è possibile calcolare la risposta del sistema a particolari ingressi del tipo (in L-trasformate):

Trovo quindi la risposta del sistema come:

Per studiare quindi la risposta al gradino delle sistema basterà moltiplicare la funzione di trasferimento per la trasformata nel dominio di Laplace del gradino unitario 1/s.

Successivamente i risultati verranno antitrasformati e diagrammati nel dominio del tempo.

Infine saranno tracciati i rispettivi diagrammi di Bode per ciò che riguarda la risposta in frequenza.

2.1 Risposta al gradino

Nota l'uscita (in L-trasformate) del sistema eccitato al gradino:

posso antitrasformate con il metodo dei residui e dei poli.

Usando il Matlab si ottengono immediatamente i seguenti valori:

Con questi valori ottengo l'espressione analitica della ristosta nel dominio del tempo:

Questa espressione è ovviamente un'approssimazione. La risposta y deve partire da 0 (poiché y è una variabile di stato e non può avere variazioni brusche anche in presenza di un ingresso brusco).

Il teorema del valore iniziale ci dice quale è l'ordine della prima derivata non nulla della risposta con la relazione:

Essa assume un valore finito per k = h + n - q - 1 dove h è il grado di integrazione dell'ingresso rispetto all'impulso, 1 per il gradino, n è il grado del denominatore e q quello del numeratore. In questo sistema k vale 5.

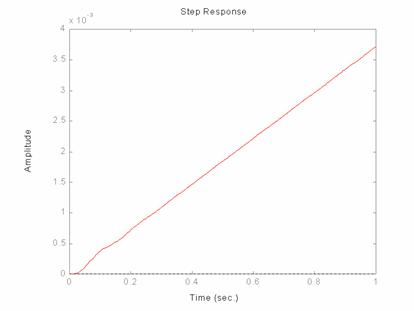
Per diagrammare la risposta in modo più preciso si usa quindi il comando "step" del Matlab, con il quale otteniamo:

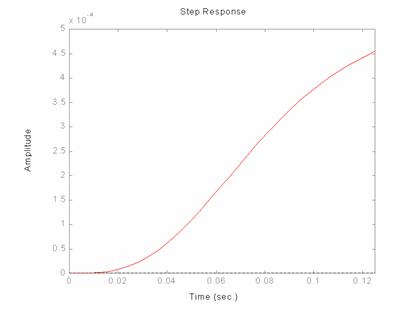
Per vedere meglio cosa accade nei pressi dell'origine:

Per vedere quale è la velocità con la quale la risposta cambia il suo andamento, devo derivare la v(s), che nel dominio delle frequenze equivale a moltiplicare la v(s) per s. Ovviamente essa corrisponde alla risposta all'impulso della G(s) (finzione di trasferimento) da cui si era partiti. Graficamente:

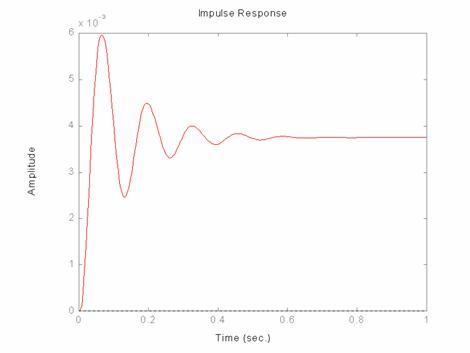
Diagrammi di Bode di G(s)

Per vedere cosa succede al variare della frequenza occorre disegnare i diagrammi di Bode di modulo e fase:

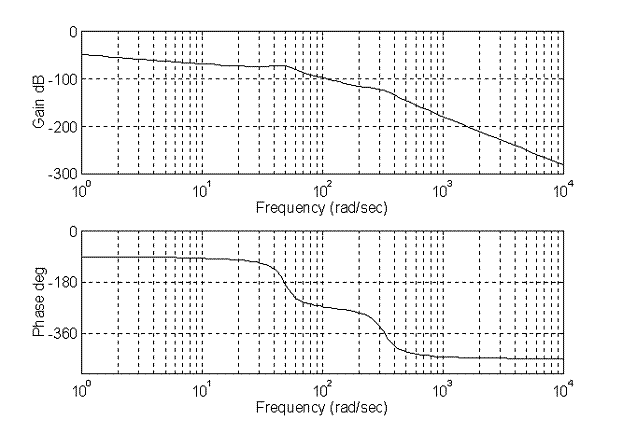
Si può osservare che il modulo della funzione di trasferimento parte con un guadagno in regime stazionario negativo, poi all'aumentare della frequenza diminuisce con pendenza -20dB/dec dovuto al polo nell'origione; passa ad una pendenza -60 dB/dec incontrando i primi due poli complessi e coniugati, finendo a causa degli altri due con una pendenza di -l00 dB/dec.

La fase parte da -90° a causa dello zero nell'origine. I successivi quattro poli la abbassano sempre più fino ad arrivare a -450°, ossia a -90° (gli angoli sono valutati con un'aritmetica circolare con 360° s 0° : si parla di calcoli in modulo 360°).

Il sistema ovviamente è privo di controllo; come dimostrano questi diagrammi andrà compensato.

3. Studio della Condizione di Stabilita' Assoluta

Si inizia ora a studiare il sistema meccanico in presenza di controllo, analizzando quindi un sistema ad anello chiuso in cui sono presenti un attuatore, un regolatore (compensatore ed un trasduttore puramente proporzionali:

Per semplicità si assume:

C(s) = K_c    A(s) = 1 T(s) = 1

Condizione indispensabile di stabilità è che tutti poli di G(s) abbiano parte reale negativa: Re(p_i) <0; andando a guardare la tabella dei poli su scritta (con l'accortezza di considerare come poli di G(s) le due coppie complesse coniugate e il solo polo nell'origine) si può facilmente notare che questa condizione è verificata.

Si procede ora allo studio della stabilità assoluta che è condizione ncessaria ma non sufficiente per una buona stabilità relativa; quest'ultima sarà valutata in seguito.

Per valutare la stabilità assoluta si usano i seguenti metodi:

Criterio di Routh

Criterio di Nyquist

Criterio del Luogo delle Radici

Criterio di Routh

Il criterio di Routh prende in considerazione la funzione di anello G_a(s) costituita dal prodotto di tutte le funzioni presenti nell'anello:

con le ipotesi prima fatte:

Posso scomporre la G_a(s) in:

Scrivi il polinomio caratteristico ad anello chiuso P(s):

Si costruisce la tabella di Routh:

dove:

La tabella di Routh completa diventa:

Ora consideriamo la prima colonna e studiamo il segno dei suoi coefficenti al variare di k:

Siccome ad ogni variazione di segno corrisponde una radice con parte reale positiva, il sistema risulta stabile se e solo se:

-l.71^.10⁵< k < 4277

ma a noi interessa che il guadagno k dell'anello sia positivo e quindi anche k_c positivo. Allora devo avere:

Criterio di Nyquist

Un modo alternativo al criterio di Routh per valutare la stabilità assoluta è quello di Nyquist. Lo strumento su cui si applica questo criterio è il cosiddetto diagramma polare del rapporto di trasferimento armonico. Questo non è altro che il luogo geometrico dei punti del piano Re(G_a)+jIm(G_a) che rappresentano G_a(jw) al variare di w da - a +

Particolare importanza assume il punto -1+j0 detto punto di Nyquist.Il diagramma di Nyquist è tracciabile a partire dal diagramma di Bode. Con l'aiuto del calcolatore si può tracciare l'andamento della parte reale e di quella immaginaria di G_a(jw) in modo più veloce. Il problema principale del calcolatore è quello di non chiudere il diagramma polare se Re(G_a) o Im(G_a) tendono ad infinito. Osservazione importante è che il diagramma di Nyquist ha sempre una forma chiusa. In ura quindi si sono indicati i punti da considerare chiusi all'infinito.

Il diagramma inoltre è stato tracciato per G_a(jw) / k , riportando quindi in ascisse ReG_a(jw) / k e in ordinate ImG_a(jw) / k. Ottengo così il punto di Nyquist che si sposta al variare di k.

Sono riportati di seguito il diagramma polare e il suo ingrandimento vicino all'origine (dal momento che assume anch'esso un'importanza rilevante):

	Diagramma polare
			w bassa
				w elevata
			w bassa

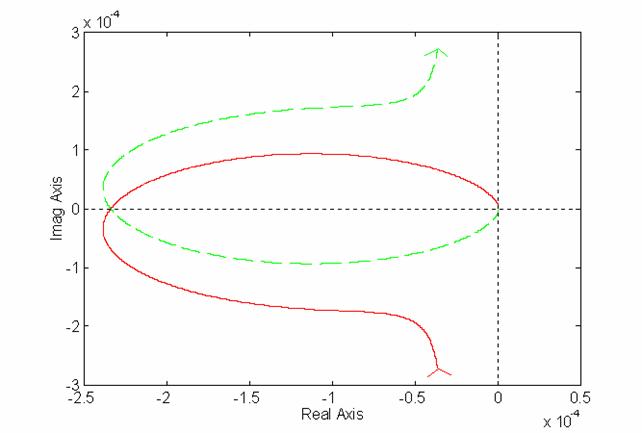
			Ingrandimento vicino all'origine
				w = 250 rad/s
	w elevata

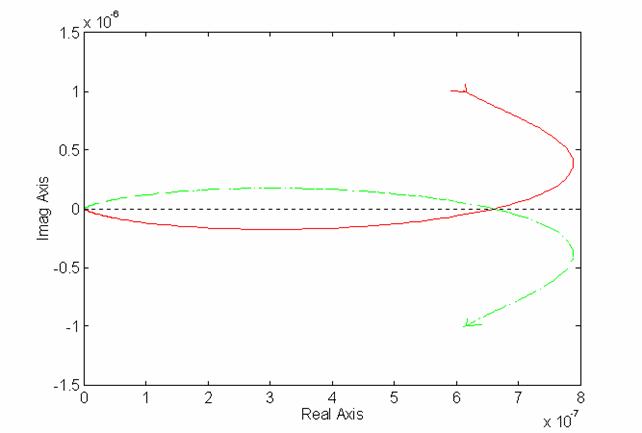
Si trovano i punti in cui il diagramma polare interseca l'asse ReG_a(jw), cioè i punti individuati dall'equazione: ImG_a(jw) = 0. Come si nota anche semplicemente guardando dal grafico, sono tre punti; si hanno allora quattro zone al variare di k. Ricordando che il diagramma era stato tracciato per G_a(jw)/k il punto di Nyquist che sul grafico ha valore 1 in realtà ha valore 1/k. In tabella si può descrivere meglio la situazione; per ogni zona è stato riportato il numero di rotazioni n_a (il numero di poli con parte reale positiva ad anello aperto), n_r (il numero di rotazioni orarie meno quello di rotazioni antiorarie del diagramma polare attorno al punto di Nyquist), n_c (il numero di poli con parte reale positiva ad anello chiuso).

Per il criterio di Nyquist n_c = n_a + n_r .

Come già visto con Routh il sistema risulta stabile solo nell'intervallo: 0 < k < 4277.

Criterio del Luogo delle Radici

Il metodo del luogo delle radici, oltre a mostrare se il sistema è stabile o no, fa vedere come si spostano i poli ad anello chiuso sul piano s al variare di k.

Si può calcolare il valore massimo ammesso per k affinchè il sistema sia stabile. La condizione di stabilità impone che tutti i poli ad anello chiuso stiano nel semipiano sinistro, perciò il valore limite di k è quello quotato nei punti in cui il luogo delle radici taglia l'asse immaginario.

Questi valori posso trovarli con l'equazione:

arg [G_a(jw)] = ±180 s

Si fa prima a puntare i punti in cui l'LDR taglia l'asse immaginario ed il calcolatore ci dice a che livello è k. Partendo dall'ipotesi che si vuole un k > 0 e ricordando che il sistema ha l'anello retroazionato negativamente, si può affermare che si deve considerare il "CASO A" e di conseguenza il diagramma del luogo delle radici sarà disegnato come tale.

	Luogo delle radici

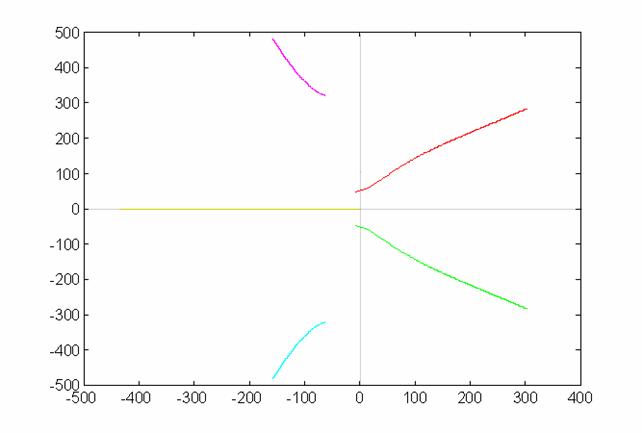
Si fa ora un ingrandimento vicino all'origine e si vanno a selezionare i punti dell'LDR che intersecano l'asse immaginario (A, B e l'origine O). Ovviamente i punti in ura rappresentano i 5 poli della G_a(s) quindi sono i 5 punti di partenza dell'LDR, corrispondenti a k = 0. Quindi nell'origine si ha un valore di k_limite= 0.

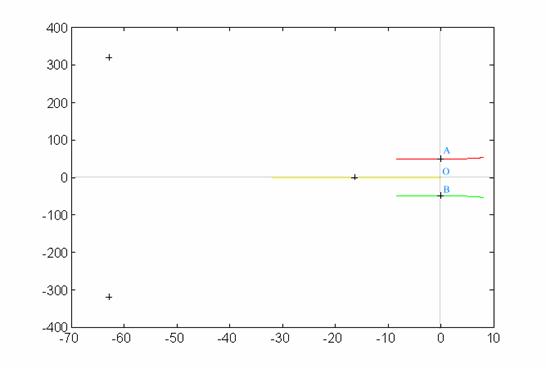
Quotando invece k nei punti A e B ed evidenziando quindi con una crocetta i poli ad anello chiuso individuati con questo k, graficamente ho la seguente situazione:

In A e B ho un valore di k_limite= 4263.

I poli ad anello chiuso corrispondenti a questo valore sono:

-62.83 + 320.69i

-62.83 - 320.69i

-0.03 + 48.50i

-0.03 - 48.50i

-l6.29

Da questi valori si può osservare come i due poli complessi e coniugati più lontani dall'origine si spostano molto più lentamente al variare di k (si sono spostati di pochissimo dalla posizione originaria). Inoltre gli altri due poli non sono proprio sull'asse immaginario (0.03 al posto di 0); questo è dovuto al fatto che si è lavorato con il puntatore grafico del Matlab e quindi si ha un certo errore. Il valore di k_limite è allora approssimato e si sposta di non molto dai valori precedentemente ricavati con gli altri due metodi.

Studio della Buona Stabilita' Relativa

Il diagramma di Nyquist da altre informazioni: si può valutare la buona stabilità relativa.

Si può dare un valutazione di quest'ultima attraverso:

Margine di fase

Margine di guadagno

Limitazione dei picchi di risonanza

Margine di fase

Condizione per avere una buona stabilità è: m_j 45°. Tale margine è rappresentabile con una retta passante per l'origine e con pendenza 45°. Il margine di fase di un sistema è ricavabile sul diagramma polare di G_a(jw)/k, con una circonferenza centrata nell'origine e passante per il punto di Nyquist. Tracciando una retta a 45° si ottiene un'intersezione con il diagramma per pulsazioni positive, si individua un punto la cui distanza dall'origine è pari al valore che deve avere il punto di Nyquist di quel sistema. Siccome il punto di Nyquist per il sistema è a -1/k, si ottiene il valore del k cercato.

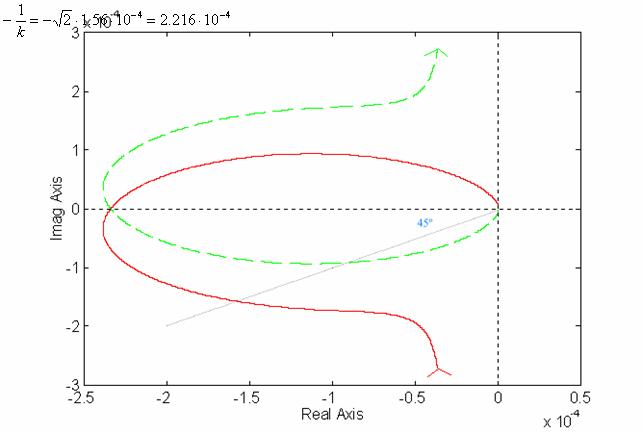
Quindi k = 4511, ma questo valore non è accettabile visto che dallo studio della stabilità assoluta si aveva k < 4277. Questa osservazione diventa veritiera osservando il diagramma polare di G_a(jw_c): se il margine di fase vale 45°, il punto di Nyquist cadrebbe tra -2.338^.10^-4 e 0, intervallo in cui il sistema è instabile.

Affinchè il sistema sia stabile il punto di Nyquist deve stare sotto il punto -2.338^.10^-4; tracciando quindi un cerchio con raggio [0, ^.10^-4], l'intersezione sul diagramma di Nyquist avviene per frequenze molto basse e con un margine di fase che è prossimo ai 90°.

Queste osservazioni sono dimostrate dalle seguenti equazioni analitiche.

Trovo la "crossover frequency" con l'equazione:

| G_a(jw_c) / k | = 1;

ottengo w_c = 0.003749 cui corrisponde

m_j arg(G_a(jw_c) / k ) + 180° = 89.998°

Utilizzando il Matlab si perviene alle stesse conclusioni.

Il valore di k_limite corrispondente è quello già trovato con il criterio di Nyquist.

Margine di Guadagno

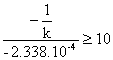
Un altro modo per stabilire la buona stabilità relativa è il margine di guadagno, definito come il rapporto tra il guadagno unitario ed il guadagno della funzione di trasferimento con la fase pari a 180°. Questo guadagno è pari al valore della parte reale del diagramma di Nyquist che taglia l'asse a parte immaginaria nulla. Per una buona stabilità deve essere m_g > 10. Nel diagramma polare il punto di Nyquist è a , occorre quindi calcolare il rapporto tra tale valore ed il valore di "taglio dell'asse reale" del diagramma. Si deve avere quindi:

Risolvendo la disequazione si ottiene m_g k . Questa imposizione è, comunque, molto meno forte di quella sul margine di fase.

Con questo valore di k si ha il diagramma alla ina successiva.

Si può costatare che con questo valore di k, il margine di guadagno vale 20 dB (pari a 10 unità) mentre il margine di fase è sempre prossimo ai 90°.

In . la fase al di sotto di -360° è riportata a 0°, è questa la ragione della spezzata.

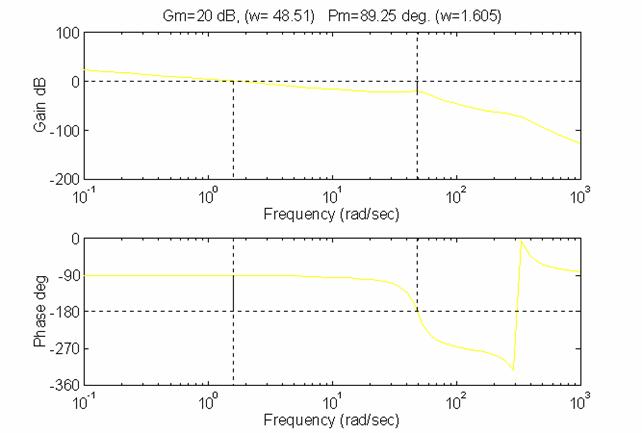
4.3 Limitazione picchi di risonanza

Lo studio dei picchi di risonanza, adifferenza dei precedenti, va fatto sulle funzioni di trasferimento ad anello chiuso. Graficamente:

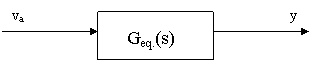
La funzione G_eq.(s) è ottenuta agevolmente con il comando "cloop" di Matlab. Ma banalmente si ha:

(i valori degli a_i sono i soliti all'inizio definiti ma in G(s) a₅ = 0 , qui a₅ = k)

Si può pensare di ricavare un guadagno k che permette d'avere un picco di risonanza pari a 3dB nella funzione di trasferimento ad anello chiuso. Per fare ciò si deve iterare ripetutamente il diagramma di Nyquist per diversi guadagni fino ad ottenere un diagramma polare tangente al cerchio M a 3dB, ossia ad un picco di risonanza di 1.4 (si ricorda che il cerchio M permette di rappresentare i luoghi a |G_eq.(s)| = cost. sul diagramma polare di G_a(s)).

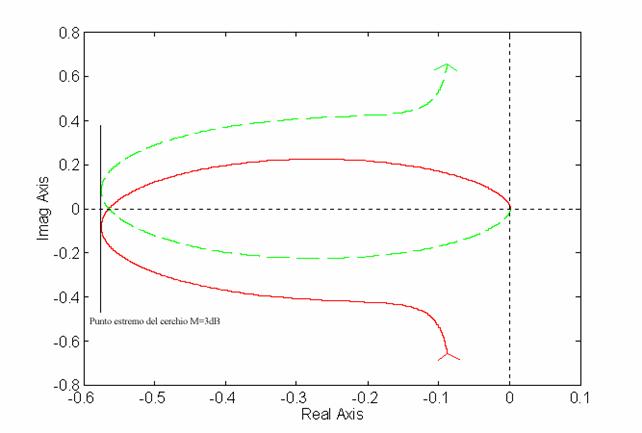
Questo diagramma di Nyquist tangente al cerchio M = 3 dB si è ottenuto ponendo k

Con un questo valore di k si hanno i seguenti margini:

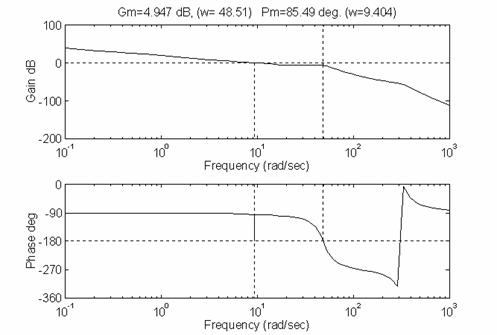
Il margine di fase vale ora 85.5°, mentre quello di guadagno vale 4.965 dB (ma è di minore importanza rispetto a quello di fase).

Il picco di risonanza, osservabile con il diagramma di Bode della funzione di trasferimento ad anello chiuso, è pari circa a 3 dB (lo si vede anche nel diagramma di Nichols). Graficamente:

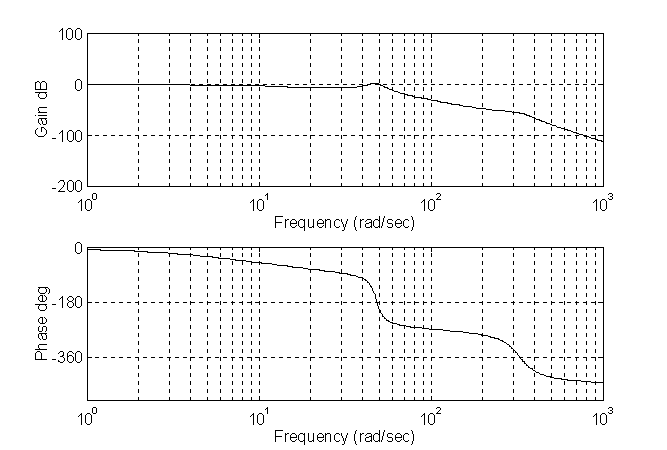
ingrandendo:

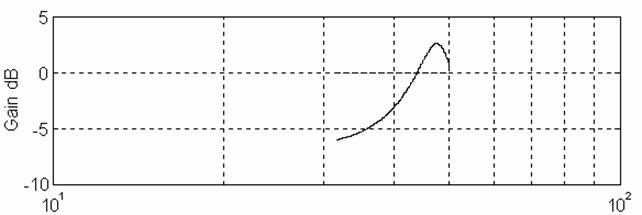
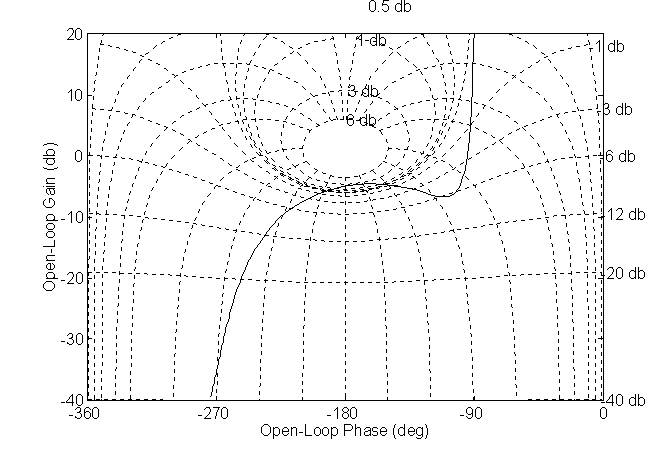
Osservandolo sulle sectiune di Nichols:

5. Progetto a livello superiore

Ci si propone ora di analizzare alcune strutture di controllo che si suppongono essere le più vantaggiose per quanto riguarda il soddisfacimento delle specifiche e la semplicità della forma del compensatore.

Compensazione in cascata

Nella compensazione in cascata di suppongono assenti i trasduttori dei disturbi (qui non presenti) e delle uscite secondarie. L'uscita del trasduttore dell'uscita primaria è confrontata direttamente con il riferimento. Graficamente:

	E		S

Schema del compensatore in cascata (in assenza di disturbi)

La funzione di trasferimento degli elementi fissi, che non è soggetta a scelta in sede di progetto, ha la seguente forma:

G_f (s)=T(s)‑G(s)‑A(s)

mentre la forma della f.d.t. dell'anello Ga (s) è:

G_a(s) = G(s)‑C(s)

dove C(s) è la f.d.t. del compensatore in cascata da progettare.

La f.d.t. ad anello chiuso tra riferimento ed uscita W(s) ha la forma:

Per tutte le suddette f.d.t. si suppone che il trasduttore T sia puramente proporzionale, ed in particolare si ipotizza:

T(s)=K_r

dove K è il rapporto di riferimento, cioè r/y.

La f.d.t. tra riferimento ed errore è:

Il tipo di sistema è determinato dal numero di zeri nell'origine della f.d.t. W(s), che in questo caso notiamo coincidere con il numero di poli di G_a(s) nell'origine. Il sistema non compensato in esame è di tipo zero in quanto G_f(s) ha un polo nell'origine.

Infine la funzione di attenuazione della sensitività ai parametri incerti vale (indipendentemente dal parametro):

Compensazione in retroazione

Questa struttura è simile alla precedente, tranne il fatto che il blocco di compensazione è in cascata al trasduttore dell'uscita primaria, come si vede in ura.

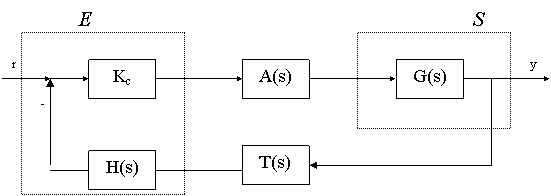
Schema del compensatore in retroazione (in assenza di disturbi)

La funzione di trasferimento degli elementi fissi è uguale a quella del compensatore in cascata, mentre le altre fd.t. diventano:

G_a(s) = G_f (s)‑H(s)‑ K_c

Con questa struttura è possibile scegliere il tipo di sistema; si può scegliere H(s) in modo che sia introdotto il numero di poli desiderato nell'origine di W_e(s). Nel nostro caso ciò non importa in quanto il sistema deve rimanere di tipo uno.

Lo svantaggio rispetto alla compensazione in cascata è che la sensitività ai parametri incerti risulta di solito più elevata; l'espressione di P(s) è analoga a quella della compensazione in cascata ma cambia ovviamente la forma della G_a(s).

Altri tipi di strutture

Si possono usare altri tipi di strutture come la retroazione dalle variabili di stato e riferimento filtrato o strutture miste. La retroazione dagli stati ha il vantaggio di non dover progettare alcun blocco dinamico e di avere una attenuazione dei parametri incerti abbastanza forte ma non è una specifica del problema in esame; inoltre questa struttura richiede dei calcoli troppo elaborati che rendono complessa la progettazione, soprattutto nel nostro caso in cui le variabili di stato sono cinque. Il riferimento filtrato permette come la compenzione in retroazione di scegliere il tipo di sistema ma non è quello che qui serve. Le strutture miste non sono prese in considerazione poiché non servono eccessivi gradi di libertà per risolvere le specifivhe del problema.

In conclusione, viste le poche specifiche da rispettare, ci si accontenta di usare la struttura con compensatore in cascata .

Progetto a livello intermedio e livello inferiore

Si sceglie la forma della funzione di trasferimento ad anello chiuso tra riferimento ed uscita e si scelgono i parametri in modo tale da poter soddisfare alle specifiche del problema. Una volta ricavati tali parametri si trova la funzione di trasferimento del sistema ad anello aperto.

Prima di usare la sintesi diretta si è cercato di vedere cosa succedeva compensando il sistema con un compensatore in cascata di tipo standard:

il compensatore in cascata a banda integrativa permette di ottenere un errore alla rampa entro le specifiche con un guadagno sufficientemente alto; tuttavia questo compensatore lascia intatto il luogo delle radici e quindi non era possibile ottenere dei poli ad anello chiuso con uno smorzamento inferiore a 0.4 (limite per il margine di buona stabilità).

il compensatore in cascata a banda derivativa sistema non permette di ottenere il soddisfacimento della specifica circa l'errore a regime (questo interviene sul sistema a medie ed alte frequenze ma non modifica il comportamento a regime) ed inoltre introduce margine di fase non necessario al sistema studiato; tuttavia questo compensatore inizia a modificare il luogo delle radici anche se non riesce del tutto ad attrarre i poli ad anello chiuso all'interno dell'area con coefficiente di smorzamento pari a 0.4.

il compensatore in cascata a banda integrativa-derivativa semplice non permette di soddisfare le specifiche sulla buona stabilità. Ma combinando la variazione del luogo delle radici del compensatore a banda derivativa e l'aumento del coefficiente di velocità del compensatore a banda integrativa permette un soddisfacimento delle specifiche.

Si dovrà quindi usare un compensatore che lavora più o meno come quest'ultimo descritto, ma, vista la non immediata soluzione del problema, si passa ad usare prima il metodo della "sintesi diretta" (che serve da approccio alla forma del compensatore) e poi il metodo per "tentativo e verifica".

Approccio mediante sintesi diretta

Si può scegliere la f.d.t. ad anello chiuso con cinque poli senza alcuno zero, poiché per la realizzabilità fisica del compensatore in cascata la differenza tra numero di poli e numero di zeri deve esssere almeno pari a quella presente nel sistema.

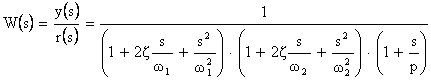
Si è posto un solo coefficiente di smorzamento pari a 0.5 ed inoltre w < w < p.

La specifica sulla buona stabilità è soddisfatta dalla scelta di z = 0.5 che impone un picco di risonanza abbastanza ridotto.

La specifica del sistema sulla precisione a regime impone un errore della risposta alla rampa a inferiore a

L'errore della risposta alla rampa vale:

Nella condzione di ugualianza p vale:

Ovviamente p, w e w₂ per come è stata definita W(s) devono essere positivi affinchè i poli ad anello chiuso abbiano parte reale negativa; questo implica che il denominatore della precendete espressione deve essere positivo:

Siccome w è positiva anche il denominatore di quest'ultima deve essere positivo, allora: w > 83.

Per rispettare le specifiche si possono scegliere come valori:

w = 120 rad/s

w = 300 rad/s

p = 3500 rad/s

Con questi parametri ho un errore alla rampa a regime di circa 1.195 10^-2 . La W(s) vale:

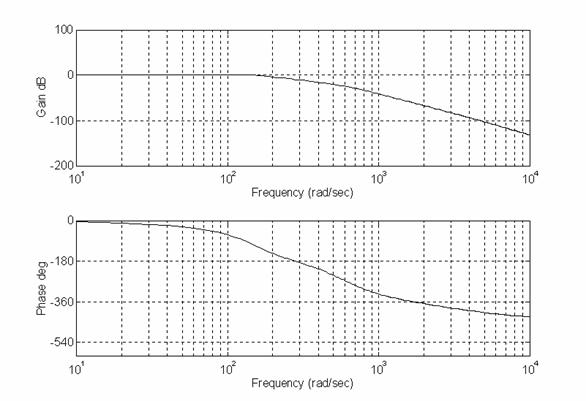
Il diagramma di Bode della W(s) così definita:

Ingrandendo nell'intervallo di frequenze compreso tra 50 rad/s e 195 rad/s si nota la banda passante w_b = 195 rad/s e un picco di risonanza che non tocca neanche i 2 dB.

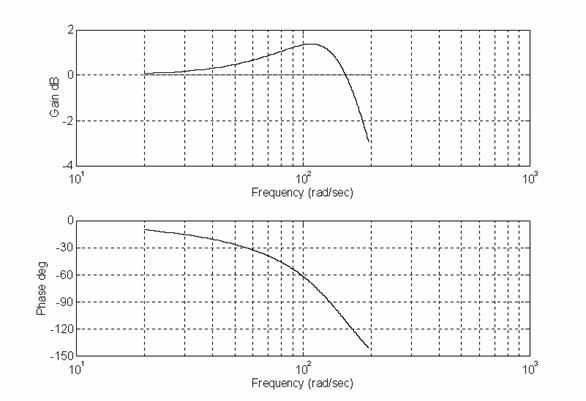
La risposta al gradino unitario y_r = W(s)/s ha il seguente grafico:

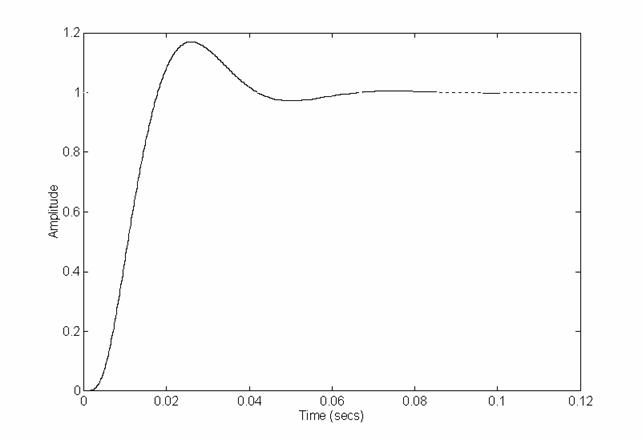
Dal quale si osserva agevolmente che la sovraelongazione massima S è inferiore a 0.25, indice di un buon margine di stabilità.

Si passa ora a ricavare la funzione di trasferimento del compensatore in cascata:

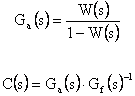
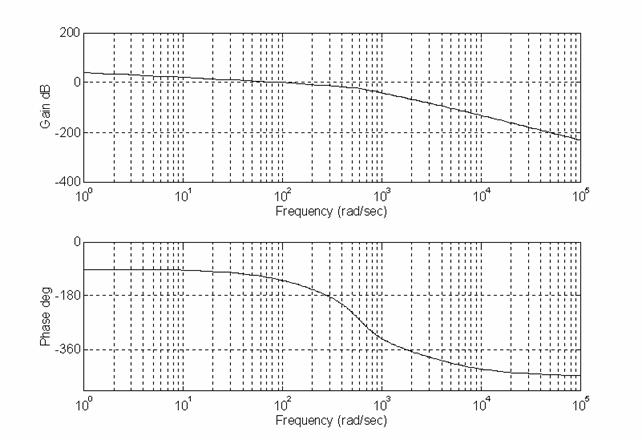
La funzione di trasferimento del sistema ad anello aperto G_a(s) vale:

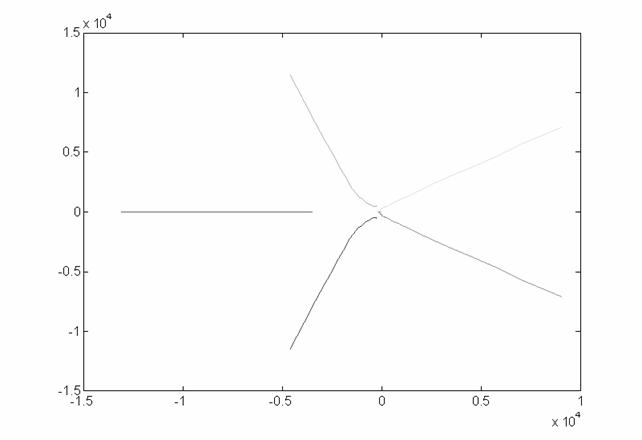
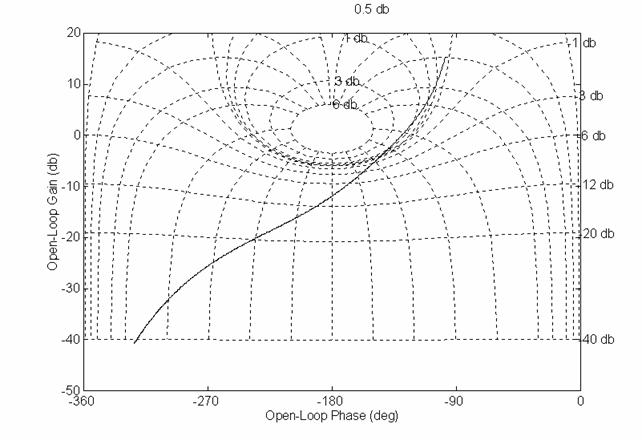
Dal diagramma di Bode, dal luogo delle radici e dalla carta di Nichols si osserva come questa funzione ad anello aperto dia la conferma di una buona stabilità relativa.

si ottiene:

Il problema di questo compensatore è di avere degli zeri che vanno a cancellano i poli complessi coniugati del sistema degli elementi fissi. Siccome questi poli hanno uno smorzamento molto basso, è rischioso cancellarli: una variazione dei parametri potrebbe portare il sistema ad oscillare troppo.

La sintesi diretta è però servita da approccio perché ha dato l'idea di mettere nel compensatore degli zeri complessi coniugati in modo da attrarre i poli ad anello chiuso nella zona con x < 0.4.

Approccio mediante "Tentativo e Verifica"

Con il metodo del "tentativo e verifica" si cerca di modificare opportunamente il luogo delle radici del sistema in modo da attrarre, con opportuni accorgimenti, i rami all'interno della fascia con smorzamento x > 0.4. Il compensatore progettato con la sintesi diretta da già l'idea che il compensazione dovrà essere a una banda derivativa multipla.

L'accorgimento che si dovrà avere usando questo metodo è l'ottenimento di un tempo di salita ragionevole senza portare il sistema a oscillare troppo.

Si suppone che il compensatore abbia solo zeri con parte reale negativa e, affinchè esso sia ficamente realizzabile, un corrispondente numero di poli ovviamenete con parte reale negativa.

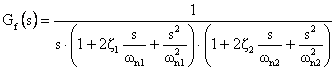
La funzione di trasferimento degli elementi fissi G_f(s) = A(s) G(s) T(s) = G(s) (con le ipotesi fatte inizialmente) si può anche scrivere nella forma:

con:

x₁ = 0.17

x₂ = 0.19

w_n1 = 326.65

w_n2 = 48.98

Si possono allora scegliere i quattro zeri del compensatore sull'asse reale negativo, due a distanza w_n1 e altri due a distanza w_n2 . I quattro poli si prendono sempre sull'asse reale negativo ma a distanza sufficentemente lontana in modo da non respingere i poli ad anello chiuso vicino all'origine e quindi da non andare ad intaccare tutto il lavoro che si sta facendo nei pressi.

Il compensatore assume la forma :

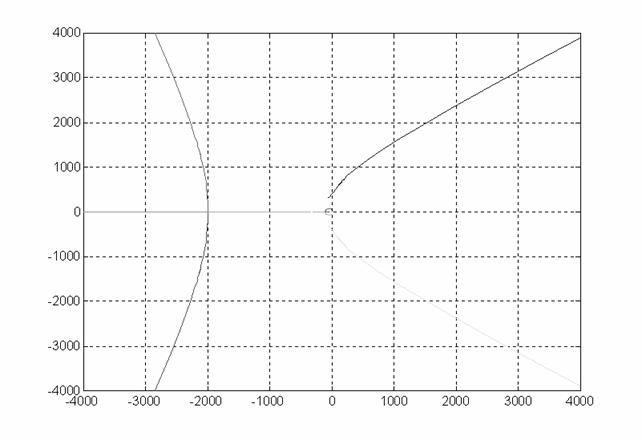
Si può osservare come è modificato il luogo delle radici nei pressi dell'origine:

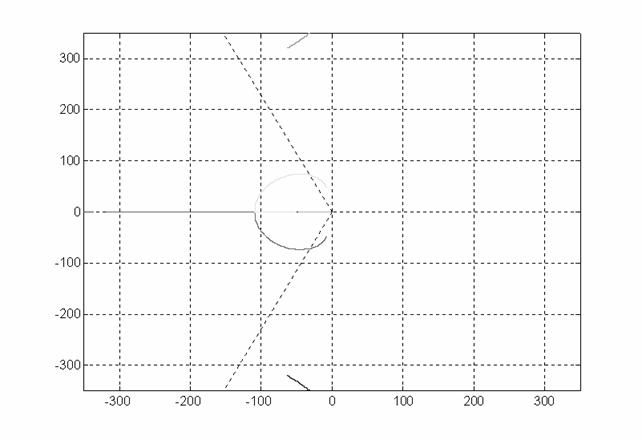
Come si può notare due poli sono attratti bene ma gli altri due rimangono ancora al di là di x

7. Progetto del Compensatore in cascata

Dal precedente tentativo quindi si è capito che inserendo nel compensatore poli e zeri solo sull'asse reale si attraggono i rami del luogo delle radici all'interno della fascia a smorzamento 0.4, ma non abbastanza, ottenendo così una risposta del sistema ancora non accettabile.

Si può pensare allora di inserire degli zeri complessi coniugati per attrarre i poli ad anello chiuso: si possono usare degli zeri simili a quelli del compensatore ricavato con la sintesi diretta ma tali da non cancellare i poli complessi coniugati e da attrarli all'interno della zona a coefficiente di smorzamento maggiore di 0.4.

Zeri: due in -30 j50 e due in -120 260j

Poli: quattro in -5000

Il luogo delle radici è il seguente:

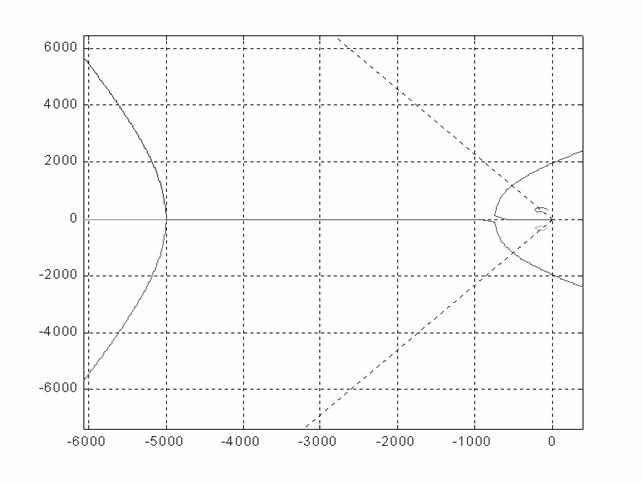
Ingrandendo nella zona vicino all'origine si può notare come gli zeri del compensatore attraggono i poli ad anello chiuso.

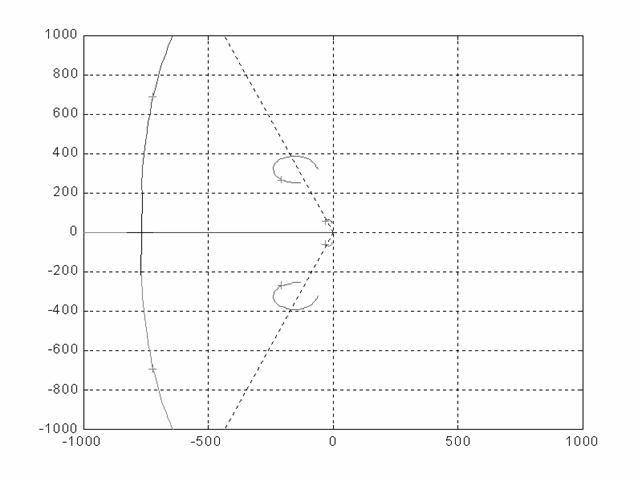
Si va a quotare ora il guadagno da assegnare al compensatore per avere lo smorzamento maggiore di 0.4. Si ha un valore di guadagno infinito pari a circa K^* = 3.67 , a cui corrisponde un coefficiente di velocità K_v = 750 e quindi un errore alla rampa a (la specifica è ampiamente soddisfatta). Tale guadagno porta i poli ad anello chiuso nella posizione illustrata nella ura sopra (è ovvio che vi sono altri due poli assai lontani dall'origine su due rami che nell'ingrandimento non sono indicati).

Vengono ora descritte le due funzioni di trasferimento ad anello aperto e anello chiuso:

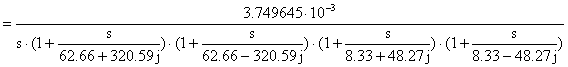
Quindi k ^*_f = k _f costF. dove costF = 256024237.

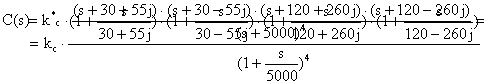
Quindi k ^*_c = k _c costC. Dove costC = 1941898.4 .

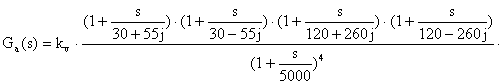
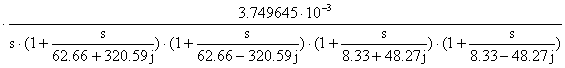
Per passare da guadagno infinito a quello stazionario semplicemente:

k_v = k _c k _f (k ^*_c k ^*_f ) / (costC costF) = K ^* / (costC costF) = 750.

L'espressione della W(s):

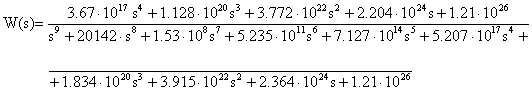
Vengono di seguito riportati i diagrammi significativi:

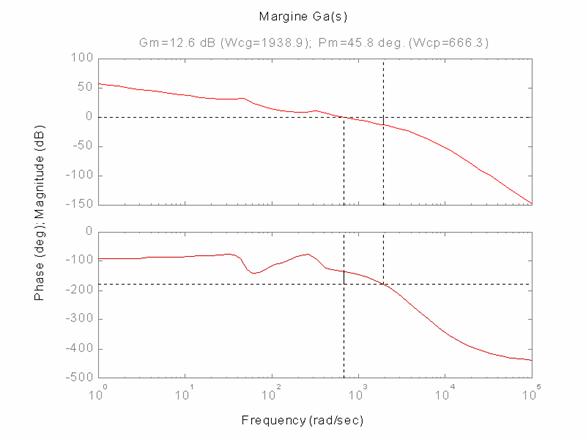
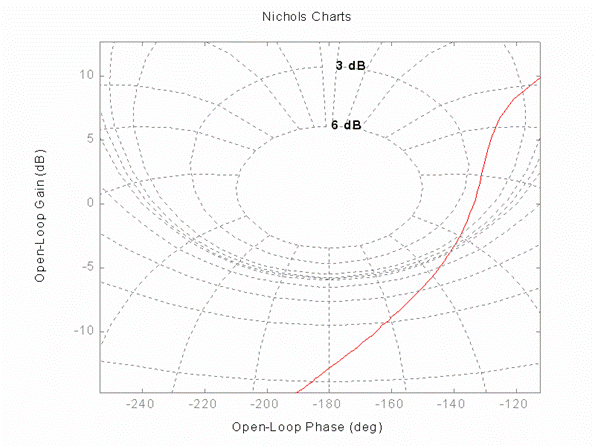
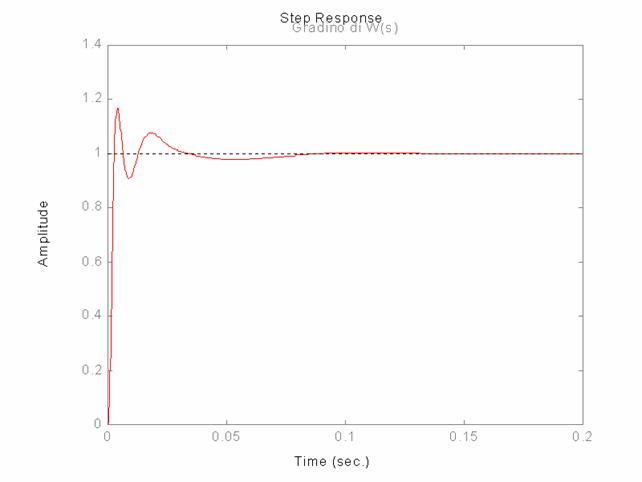
Prestazioni del sistema compensato:

Il tempo di assestamento e di salita caratterizzano la rapidità di risposta, così anche la banda passante che non deve essere nè troppo piccola (per evitare tempi di risposta eccessivi) nè troppo ampia (per evitare tempi eccessivamente ristretti); in tal caso si potrebbero verificare rotture nel sistema meccanico. Nel nostro caso la banda passante risulta ampia ma, come si legge dai tempi di risposta, non c'è una sollecitazione eccessiva del sistema meccanico.

Il compensatore progettato è un compensatore a banda derivativa quadrupla con poli complessi coniugati: le specifiche standard sul margine di fase, picchi di risonanza e sovraelongazione massima sono rispettati; la specifica sul margine di guadagno è di poca importanza ma è sforata di non molto. L'unica specifica data dal problema è ampiamente soddisfatta.

Verifica del Compensatore analogico

1^a Verifica: Analisi della W_r,c

Per la verifica si può valutare il comportamento della grandezza pericolosa comando: nel sistema in studio il comando è la corrente d'alimentazione del motore elettrico. La funzione di trasferimento tra il riferimento ed il comando è

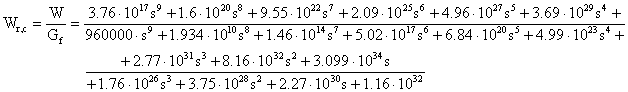
Il modulo di tale funzione di trasferimento è riportato di seguito e pare a prima vista elevato ma è una diretta conseguenza dei valori tipici del sistema meccanico sotto controllo per cui non deve spaventare ma solo avvisare di dimensionare adeguatamente le protezioni.

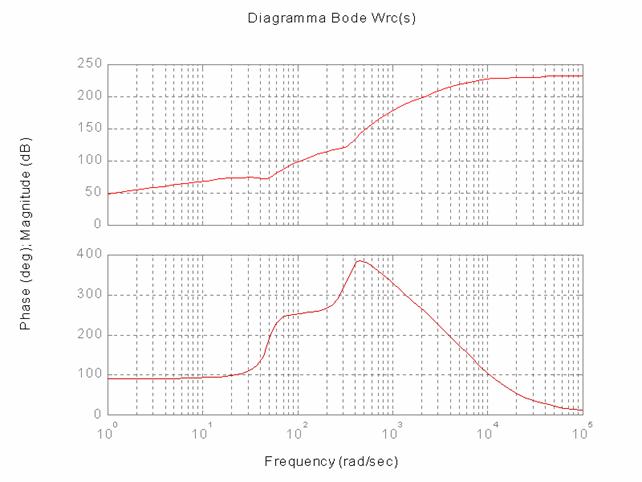
2^a Verifica:Analisi della risposta al gradino con parametri di G(s) modificati

Un'altra verifica che si è ritenuta utile svolgere è il controllo della funzione di attenuazione della sensitività ai parametri incerti. Bisogna vedere cosa accade al variare di alcuni parametri del sistema ovvero al variare della posizione dei poli complessi coniugati (x piccolo) della funzione di trasferimento degli elemnti fissi.

Se si spostano tali poli in 0, -62 j310, 8.33 48.27j (si sono modificati i primi due poli) e si è ottenuta la seguente risposta al gradino:

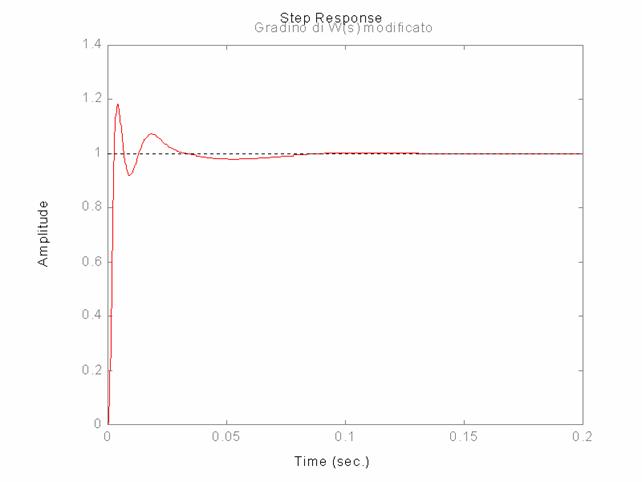
Tale riposta si discosta di pochissimo da quella precedente, indice di un buon controllo.

3^a Verifica: Analisi della P(s)

Un ulteriore metodo per verificare come il sistema risponde alla variazione dei parametri è quello di valutare la sensitività ai parametri incerti. L'espressione della funzione di attenuazione ai parametri incerti P(s) vale:

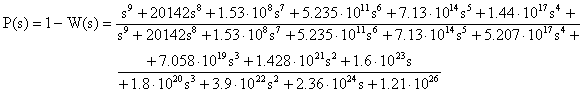
L'andamento del suo modulo:

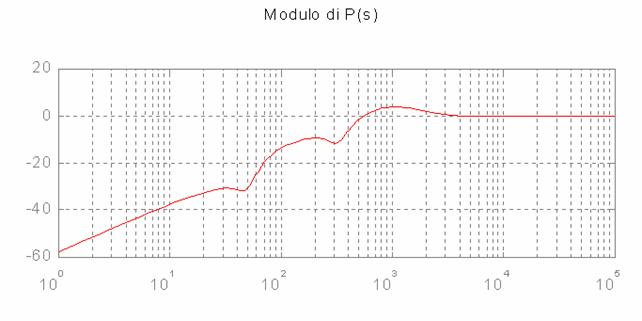
Si nota come le variazioni dei parametri siano sentite solo oltre la banda di precisione ma non si lavorerà mai oltre tale banda in quanto qui il sistema è del tutto inutile. Il sistema controllato, quindi, non è disturbato dalle variazioni dei suoi parametri.

Realizzazione digitale

Per realizzare una struttura di controllo digitale si deve sostituire al compensatore analogico un corrispondente compensatore digitale indicata con C(z). Ovviamente va inserito a valle del nuovo compensatore un dispositivo in grado di convertire i segnali digitali in analogici: il dispositivo di tenuta di ordine zero (zero order hold). Questo dispositivo ricostruirsce il segnale analogico partendo dalla sequenza di impulsi in uscita dal compensatore digitale. La sua funzione di trasferimento risulta:

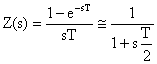
dove T è il periodo di campionamento. Mediante una regola derivata dall'applicazione del Teorema di Shannon si trova:

dove w_b è la banda passante del sistema controllato. T è il periodo di campionamento che consente una corretta ricostruzione del segnale analogico partendo da quello digitale.

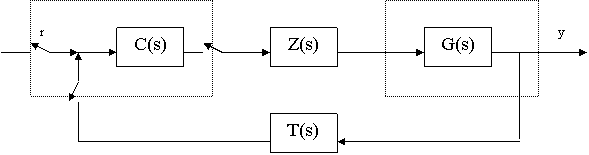
Schema a blocchi per il controllo digitale.

Il compensatore che sarà progettato conterrà soltanto zeri, non è quindi fisicamente realizzabile ma permette di ottenere una buona risposta del sistema in esame. Verrà quindi progettato un nuovo compensatore analogico e poi sarà trasposto nell'ambito digitale.

Progetto del Compensatore Analogico

Si possono mettere i quattro zeri del compensatore sull'asse reale negativo, due a distanza w_n1 e altri due a distanza w_n2 .Il compensatore assume la forma :

Le specifiche i progetto imponevano che fosse verificato l'errore di inseguimento della rampa a regime: a . Siccome è una struttura di compensazione in cascata, a vale:

Questa specifica si traduce nella scelta del guadagno k_c da attribuire al compensatore.

La f.d.t. ad anello aperto ha l'espressione:

Il sistema così compensato ha il seguente luogo delle radici nei pressi dell'origine:

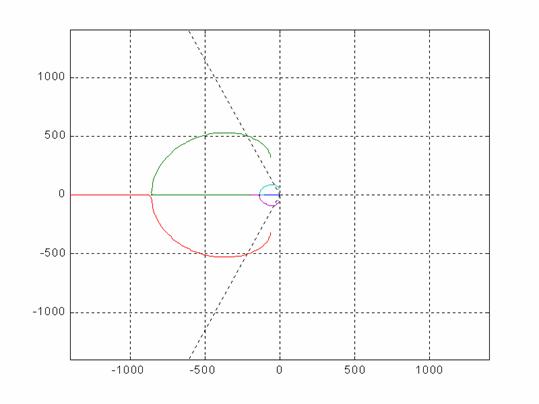
Si può vedere che i rami dei poli ad anello chiuso sono attirati dalle due coppie di zeri sull'asse reale tutti entro la fascia di smorzamento x £ 0.4. Quotando il guadagno vicino alla zona x = 0.4 si ottiene un coefficiente di velocità che vale circa 1000.

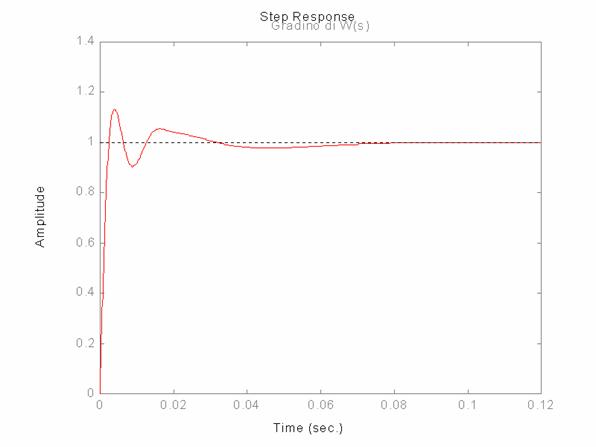
Di seguito sono riportati i diagrammi significativi:

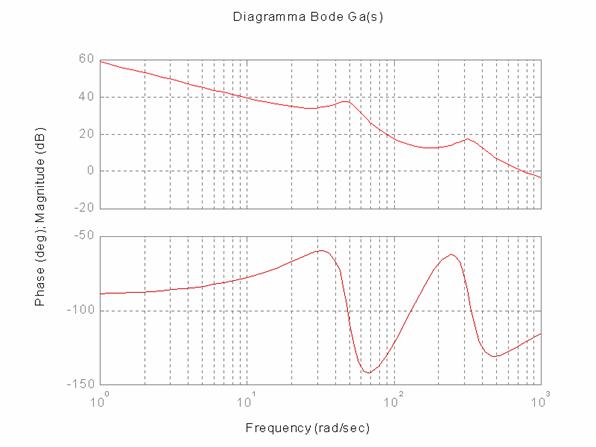
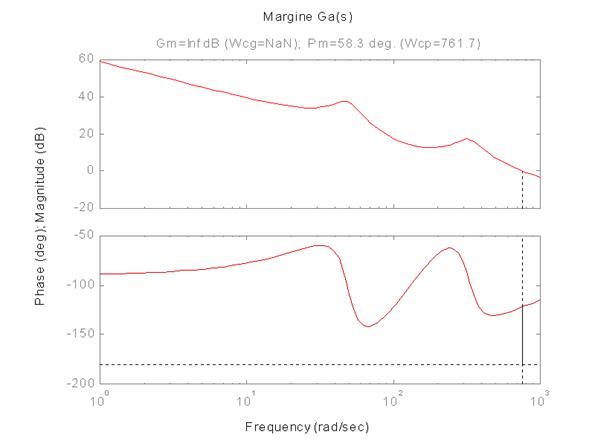
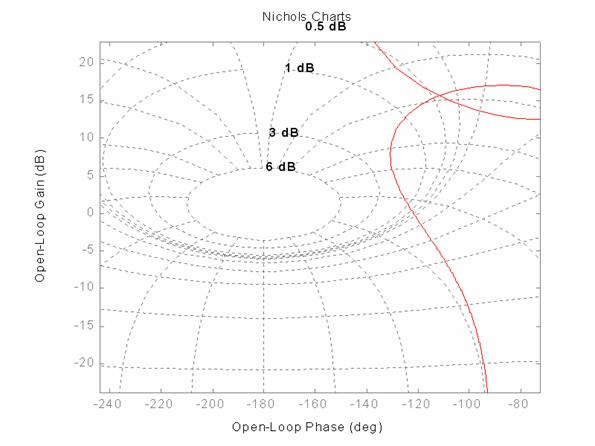
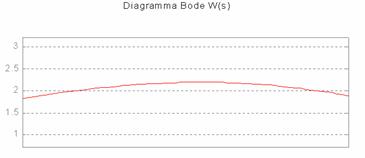
Il picco di risonanza è evidenziato anche dal diagramma di W(s):

Dall'esame del diagramma di Bode in catena chiusa si trova anche:

Il passo di campionamento da utilizzare e la corrispondente frequenza valgono:

Si sceglie:

Inserimento del dispositivo di tenuta

Il dispositivo di tenuta Z(s) è inserito in cascata con il compensatore; quindi va ad aggiungere un polo al compensatore e quindi alla funzione di trasferimento ad anello aperto. Si deve ora controllare che Z(s) non causi un effetto destabilizzante.

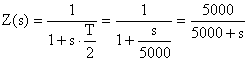
Il luogo delle radici diventa:

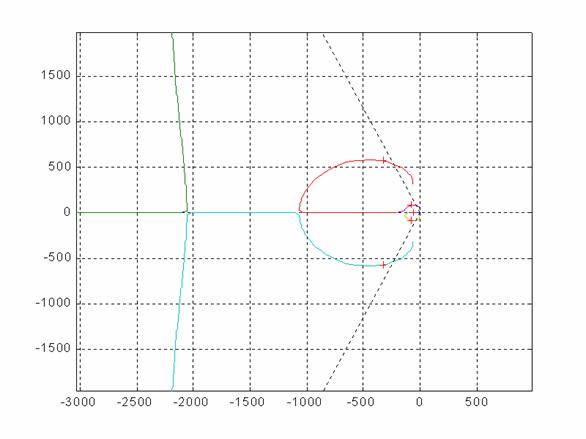
Nelle ine seguenti sono riportati di diagrammi più significativi.

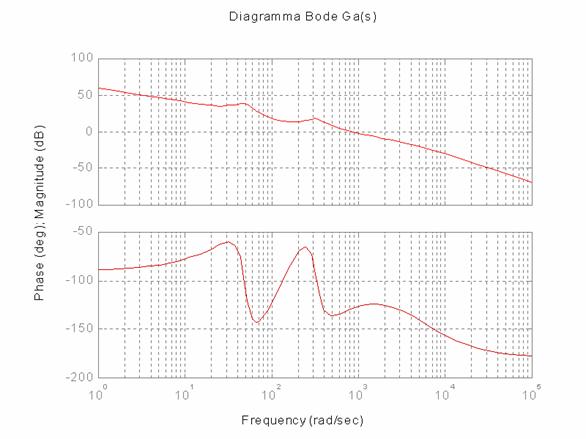
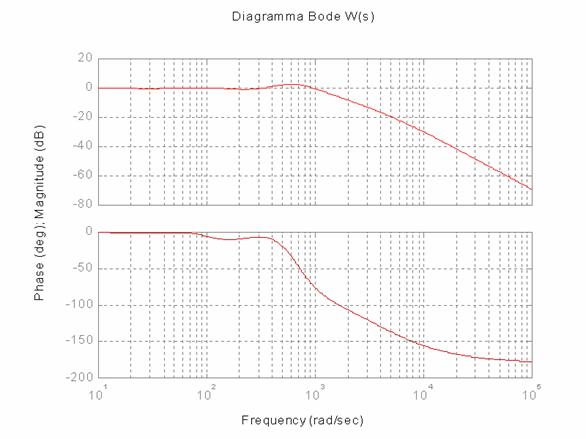
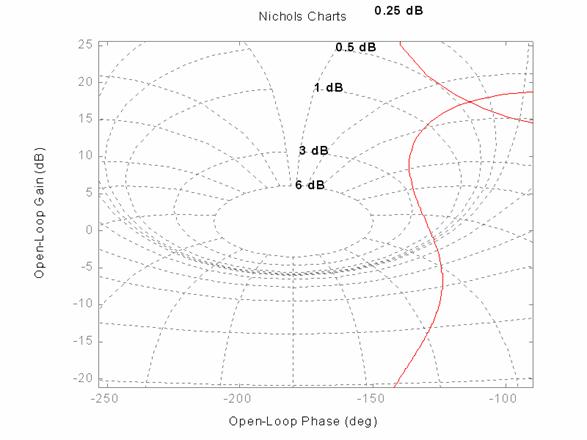
Il picco di risonanza (già osservabile sulla carta di Nichols):

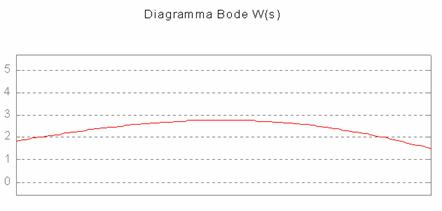
Il tutto è stato ottenuto con un guadagno k_c = 7.2

L'inserimento di questo dispositivo ha determinato una diminuzione del margine di fase e un aumento del picco di risonanza ma nonostante ció tutte le specifiche sono ampiamente soddisfatte.

Determinazione della C(z)

Si passa ora alla realizzazione digitale vera e propria del compensatore: basta convertire la f.d.t. del compensatore analogico nella corrispondente in ambito di trasformata Zeta. Nel nostro caso il compensatore analogico ha quattro zeri reali, per cui vale:

Si tratta di una funzione di trasferimento impropria.

Metodo dell'Invarianza della Risposta ad Ingressi Tipici:

Se si invia un impulso in ingresso a questo sistema si ottiene:

Antitrasformando questa espressione si ha una combinazione lineare di impulsi e loro derivate, che non hanno una corrispondenza nella trasformata Zeta. Non si può usare il metodo dell'invarianza della risposta agli ingressi tipici ad una C(s) impropria, a meno che non si utilizzano segnali di ingresso di ordine superiore, che però non garantiscono, nelle loro trasformate Zeta, l'alternanza dei segni dei coefficienti.

Metodo delle Differenze in Avanti:

Dalla C(s) si ottiene subito C(z) con la seguente sostituzione:

Si riporta per semplicitá la funzione C(s), contenente anche il guadagno prima determinato:

Sostituendo si ottiene:

Calcolando l'eventuale costante aggiuntiva:

Non è quindi necessaria alcun k aggiuntivo. Questa verifica é inutile nei metodi delle differenze, della trasformazione bilineare di Tustin con e senza precompensazione in frequenza, perché con le sostituzioni fatte é sempre garantita in modo automatico. E' necessario calcolare tale limite nel metodo della trasposizione dei poli e degli zeri.

I coefficienti della C(z) risultano:

Metodo delle Differenze all'Indietro:

Dalla C(s) si ottiene subito C(z) con la seguente sostituzione:

Ricordando che C(z) assume la seguente forma:

dove i valori dei coefficienti risultano:

Il fatto che f₀ sia nullo, comporta che il sistema è anticipativo, condizione non accettabile per un sistema fisico. Si potrebbe ritardare il campionamento di 4 istanti T ma questo pare eccessivo, per cui si esclude tale trasformazione dalla realizzazione pratica.

Metodo della Trasformazione Bilineare (o di Tustin):

Dalla C(s) si ottiene subito C(z) con la seguente sostituzione:

I coefficenti della C(z) valgono:

Metodo della Trasformazione Bilineare (o di Tustin) con Precompensazione in Frequenza:

Si è utilizzato un valore di w = 200 rad/s. La scelta è stata indicata dal fatto che i diagrammi di Bode delle f.d.t. del compensatore in ambito analogico e digitale tendono a distanziarsi per pulsazioni elevate. Siccome le pulsazioni significative del nostro compensatore sono quelle degli zeri 100 e 200 rad/s, si è scelta pulsazione w₁ = 200 (fino a questa pulsazione i diagrammi di Bode non saranno eccessivamente diversi).

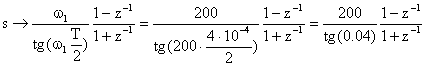
Dalla C(s) si ottiene C(z) con la seguente sostituzione:

Affinchè l'approssimazione si valida l'argomento della tangente deve essere molto piccolo, infatti :

I coefficenti della C(z) valgono:

Metodo della Trasposizione dei Poli e degli Zeri:

Siccome la C(s) presa in considerazione ha solo quattro zeri reali, si opera la seguente sostituzione:

I coefficenti della C(z) valgono:

Eseguendo i limite delle f.d.t. dei due tipi di compensatori si ottiene:

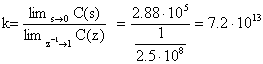
I due limiti coincidono se k = 7.2 10¹³, dove

Indicando con C_n(z), la C(z) ottenuta trasformando C(s) con la sstituzione sopra scritta.

Come nel metodo delle differenze all'indietro f₀ risulta nullo e ciò comporta che il sistema diventi anticipativo, condizione non accettabile per un sistema fisico. Anche qui si potrebbe ritardare il campionamento di 4 istanti T ma è una approssimazione troppo alta, per cui si esclude tale trasformazione dalla realizzazione pratica.

Prove di Validazione

Una volta proposta la realizzazione digitale del compensatore analogico, si deve verificare la validità delle trasformazioni. Si sceglie un opportuno segnale di prova da utilizzare in modo che possa simulare bene i segnali veri e propri di ingresso del sistema. Questo segnale di prova deve avere limitata escursione, rapidità di variazione e semplicità nella forma: si utilizza quindi un segnale a rampa tagliata.

Osservazione importante è che il compensatore analogico ha una f.d.t. impropria (cioè ha una azione derivativa), allora conviene fare in modo che il segnale citato risulti come uscita del compensatore e non come ingresso, perché altrimenti l'uscita risulterebbe discontinua nel tempo e il confronto tra uscita digitale e analogica sarebbe molto difficile.

La trasformata di Laplace del segnale a rampa tagliata risulta:

L'aspetto di tale segnale è il seguente:

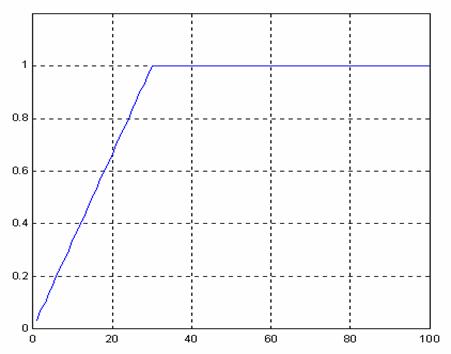
In realtà con l'espressione analitica della y(s) su scritta, lo spigolo non esiste e antitrasformando si ottiene la y(t) (uscita del compensatore analogico) dalla si prenderanno i campioni y(kt).

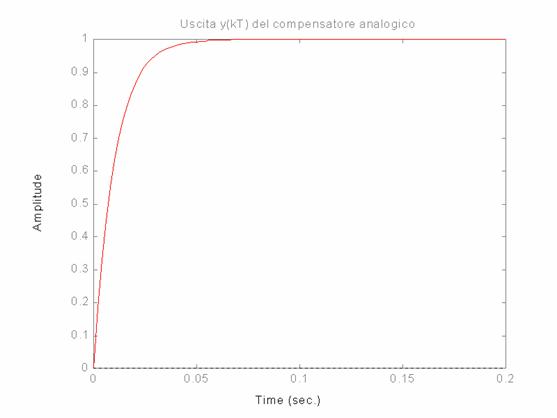
Il grafico effettivo della y(t):

Ora si sta analizzando solo il comportamento del compensatore digitale, quindi ingressi ed uscite si riferiscono al solo compensatore; si ha quindi il seguente schema:

Si fa y(s) = C(s) u(s), allora l'ingresso deve essere:

Dove F è la durata del "fronte" di salita del segnale ed è legata a T (passo di campionamento) tramite F = n T e scegliendo n =50 :

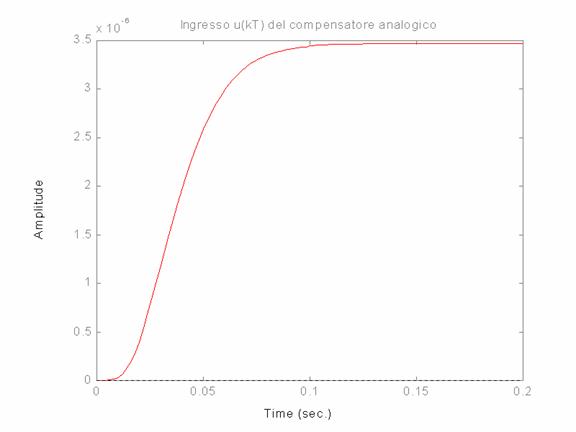
L'andamento del tempo dell'ingresso u(t):

Si calcola ora l'andamento nel tempo delle u(t) e y(t) e ponendo t = kT si considerano i campioni u(kT) e y(kT) del segnale continuo. D'altraparte si possono ottenere le uscite digitali y^*(kT) utilizzando la funzione C(z) partendo dai campioni u(kT).

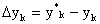
Le differenze fra i campioni analogici e digitali risultano:

la quale varia a seconda del metodo di discretizzazione adoperato.

Di seguito sono riportati i casi fisicamente realizzabili eliminando quindi il metodo delle differenze all'indietro e il metodo della trasposizione che sono anticipativi.

Metodo delle Differenze in Avanti

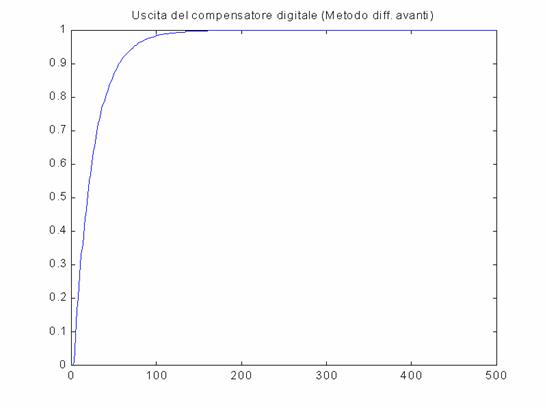
L'andamento dell'uscita digitale è il seguente:

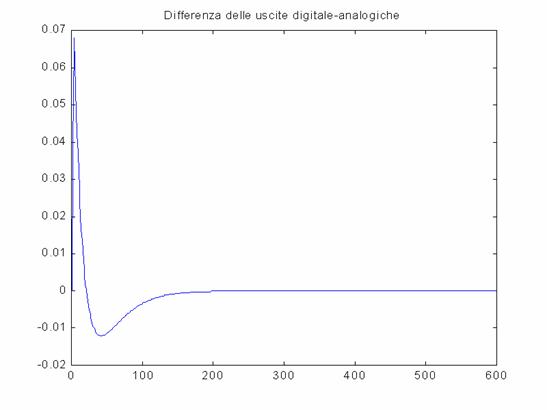
L'andamento della differenza tra uscita digitale e analogica è la seguente:

Metodo della Trasformazione Bilineare (o di Tustin)

L'andamento dell'uscita digitale è il seguente:

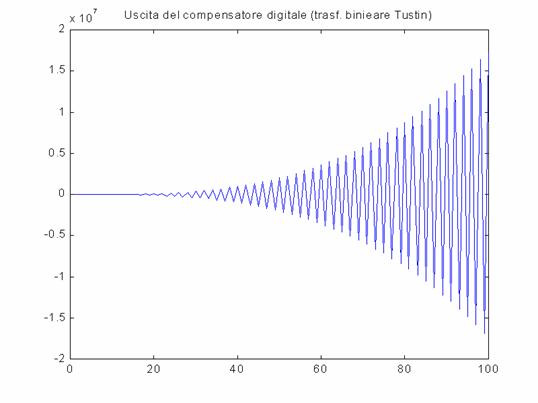
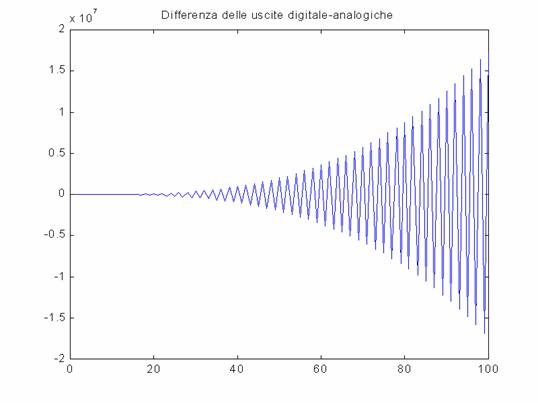
L'andamento della differenza tra uscita digitale e analogica è la seguente:

Metodo della Trasformazione Bilineare con Precompensazione in frequenza

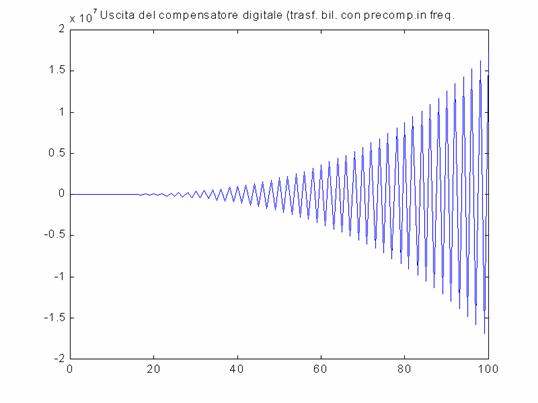
L'andamento dell'uscita digitale è il seguente:

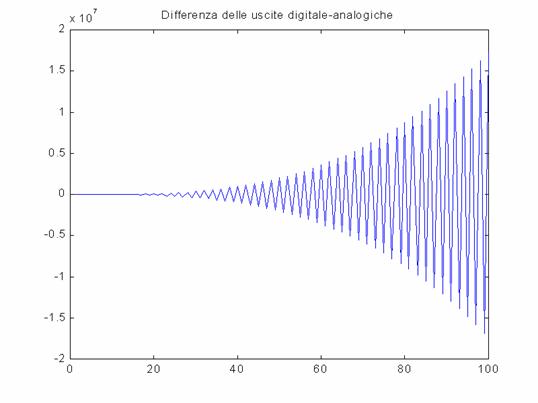
L'andamento della differenza tra uscita digitale e analogica è la seguente:

Conclusioni

Nei metodi della trasformazione bilineare si ottengono andamenti oscillanti crescenti con conseguente esplosione della differenza fra uscita analogica e digitale. Con il metodo delle differenze all'indietro e della trasposizione di poli e zeri si avrebbe la necessità di eseguire un campionamento ritardato di 4 campioni, per evitare che i sistemi risultino anticipativi.

L'unico metodo ritenuto valido è quello delle differenze in avanti: analizzando la risposta al segnale di prova delle C(z) si nota come riproduca abbastanza bene l'uscita con un errore (differenza tra uscita analogica e uscita digitale) che va a zero subito dopo la partenza. Il valore di picco dell'errore è registrato quindi in partenza e comunque ha un valore molto basso pari a 0.0681.