| tecnica |
|
modulo II
Premessa. In questo modulo vengono introdotte le principali definizioni e proprietà relative alla probabilità. Si può affermare che la teoria della probabilità rappresenta una sorta di "matematica dell'incerto", in quanto si propone di rappresentare - per quanto possibile - degli "eventi incerti" mediante dei numeri "certi" (o per lo meno calcolabili in linea di principio); tali numeri sono appunto le probabilità di tali eventi, i "valori medi" associati alle grandezze che descrivono tali eventi, ecc. Per "evento incerto (o "aleatorio", come si dice nel linguaggio probabilistico), qui si intende un evento il cui verificarsi o meno non può essere noto a priori, ad esempio: "realizzerò un ambo alla prossima estrazione del lotto", oppure "domani pioverà"; in entrambi questi esempi, per sapere se tali eventi si verificheranno bisognerà attendere la loro eventuale realizzazione. Non bisogna pensare, naturalmente, che l'incertezza riguardi solo il futuro; essa è presente ogni volta che siamo in condizioni di scarsa, o non completa, informazione: si pensi agli eventi associati ai seguenti enunciati: "questo studente non ha studiato a sufficienza" (proposizione che potrebbe essere formulata da un professore al termine di un esame), oppure "questo reperto archeologico risale al I sec. A.C." (proposizione che potrebbe essere formulata da un archeologo all'atto di un ritrovamento), oppure "Domenica scorsa la Juventus ha vinto" (evento che è incerto per una persona che non segua il calcio, o che Domenica scorsa non si trovasse in Italia, o forse per un cittadino straniero).
Come si vede, tali eventi sono esprimibili mediante proposizioni che non sono, per chi le formula, né vere né false, ma appunto "incerte". Sottolineiamo "per chi le formula" perché la mancanza di informazione assume spesso aspetto soggettivi, come è chiaro dall'ultimo esempio (per un tifoso di calcio, probabilmente il risultato dell'ultima partita della Juve sarebbe noto, e quindi "certo" il relativo evento).
A tale tipo di proposizioni incerte il calcolo delle probabilità intende associare un numero, compreso tra zero ed uno, che stia a misurare il "grado di veridicità" di una proposizione. Sotto tale aspetto, la teoria della probabilità può essere considerata come una estensione della usuale logica delle proposizioni, che assegna ad ogni enunciato il valore "vero" oppure "falso". Nell'ambito della teoria della probabilità - ovvero della matematica dell'incertezza - siamo invece, per carenza di informazioni, in condizioni appunto di incertezza, per cui, accanto a proposizioni vere (cui assegneremo probabilità 1) e false (cui assegneremo probabilità 0), avremo appunto proposizioni incerte (quali quelle di cui agli esempi precedenti), la cui probabilità sarà un numero reale tra 0 e 1, tanto più vicino ad 1 quanto più la proposizione appare, sulla base delle informazioni in possesso, vera.
Per sviluppare le regole della probabilità è necessario dapprima introdurre l'algebra degli eventi aleatori, dunque gli assiomi della probabilità e le proprietà che da essi derivano. L'impostazione assiomatica che qui si presenta, essendo quella su cui si basa il moderno calcolo delle probabilità, è utile per trattare il problema con la maggior generalità possibile: per realizzare ciò, essa prescinde da ogni possibile interpretazione fisica del concetto di probabilità, a rischio di poter apparire a prima vista piuttosto astratta; non bisogna tuttavia dimenticare che il calcolo delle probabilità, le cui finalità sono pratiche, serve a dare una impostazione quantitativa ad una problematica basata su concetti che sono intuitivi. Ad esempio, ogni persona, indipendentemente dal fatto che abbia studiato o meno la probabilità, sa cosa intende quando afferma: "è più probabile realizzare un ambo anziché un terno al gioco del lotto", oppure "è poco probabile che io riesca a ottenere un voto alto al prossimo esame".
Storicamente, la probabilità nasce dalla osservazione che molti fenomeni fisici aleatori (casuali) presentano una certa "regolarità", ovvero una frequenza piuttosto stabile nel verificarsi. Il modulo inizia dunque introducendo il concetto di fenomeno aleatorio, dunque l'algebra degli eventi aleatori e i fondamenti del calcolo delle probabilità, secondo un approccio elementare (un approccio avanzato richiede la "teoria della misura": per esso si può fare riferimento - ad esempio - al testo di Dall'Aglio, nella Bibliografia di seguito riportata).
Bisogna però osservare che molte proposizioni incerte non si riferiscono ad eventi "ripetibili". Se pensiamo alle due proposizioni sopra riportate come esempio, riguardanti rispettivamente il lotto e il risultato di un esame, ci accorgiamo che molti di noi attribuiranno significati diversi al concetto di probabilità nei due casi: nel primo si fa riferimento alla "frequenza" di un evento ripetibile (se ripeto molte volte l'estrazione di numeri al lotto, mi aspetto di ottenere più ambi che terni, ovvero la frequenza dell'ambo sarà maggiore); nel secondo ci riferiamo ad un evento chiaramente non ripetibile, di cui cioè non è realisticamente pensabile parlare di frequenza (non è possibile ripetere l'esame tante volte nelle identiche condizioni); lo stesso vale, ad esempio, quando formuliamo un pronostico su di una partita di calcio (sebbene i giornalisti sportivi si divertano a calcolare la frequenza di vittoria di una squadra "a" contro una squadra "b" nei precedenti incontri, è abbastanza ovvio che queste statistiche non hanno alcun valore - se non al più psicologico - ai fini della probabilità di vittoria di "a" nel prossimo incontro, visto che questo avverrà in condizioni diverse, con giocatori diversi, ecc.) . Anche in questi ultimi casi si può tuttavia parlare di probabilità, anche se la sua interpretazione è piuttosto "soggettiva" (opinione di chi formula il pronostico) anziché "oggettiva", come è quella che si riferisce alla "frequenza" dell'evento (frequenza che sarebbe appunto una proprietà dell'evento indipendente - ammesso che ciò sia possibile - dallo stato di informazione del soggetto che vuole calcolarne la probabilità). L'interpretazione soggettiva è storicamente successiva a quella oggettiva, ma trova sempre maggiori campi di applicazioni e seguaci tra gli studiosi (essa è trattata ampiamente nel testo di Dall'Aglio, ed è di base a quello di Scozzafava) .
E' importante in ogni caso evidenziare che la teoria della probabilità fino ad oggi sviluppata, grazie soprattutto alla impostazione assiomatica di Kolmogorov (1933) permette di lavorare bene con qualsiasi interpretazione "filosofica" della probabilità, la quale può dunque anche essere assunta come un concetto primitivo, proprio come il concetto di "punto" in Geometria, quello di "insieme" in Algebra o Analisi, ecc.
livello elementare
Spirito G. "La matematica dell'incerto", Tascabili Newton Compton, 1995
Pintacuda: "Primo corso di probabilità", Muzzio
Scozzafava "La probabilità soggettiva e le sue applicazioni " Editoriale Veschi, 1991
livello medio
Dall'Aglio G. "Calcolo delle Probabilità", Zanichelli, 1987
De Finetti B. "La Logica dell'incerto (saggi 1931-l976)", Il Saggiatore 1989
Gnedenko B. V. 'Teoria della Probabilità', Editori Riuniti, 1979.
Papoulis A. 'Probabilità, Variabili Aleatorie, Processi Stocastici', Boringhieri, 1978
(3a Edizione, in Inglese: Mc Graw Hill, N.Y., 1991.).
2.1 FENOMENI E MODELLI ALEATORI, VARIABILI ALEATORIE.
Fenomeni deterministici e fenomeni aleatori.
Dal punto di vista delle applicazioni della probabilità alla fisica o all'ingegneria, i fenomeni naturali possono essere classificati in due grossi sottoinsiemi :
i fenomeni deterministici;
i fenomeni aleatori.
Un fenomeno deterministico è un fenomeno descritto da grandezze note a priori o comunque calcolabili con esattezza. Un fenomeno si dice invece aleatorio (o casuale) quando una o più grandezze che lo descrivono sono affette da incertezza, nel senso che il loro valore non può essere conosciuto a priori (ossia prima di effettuare l'osservazione che ci consente di calcolare il valore di tali grandezze).
Un esempio di fenomeno deterministico è quello del passaggio di corrente elettrica in un conduttore, fenomeno descritto dalla legge di Ohm: se si considera un conduttore di resistenza R ai cui capi è applicata una tensione costante V, è noto che attraverso tale conduttore fluirà una corrente di intensità I = V/R; dunque, una volta note o misurate le grandezze V e R, la corrente I è nota con precisione (prescindiamo qui dall'errore di misura, che non dipende dal fenomeno; di esso tratteremo poi).
Di esempi di fenomeni aleatori ne conosciamo parecchi nell'esperienza quotidiana (ad esempio: il risultato del lancio di un dado o di una moneta, quello di una partita di calcio, il verificarsi di determinate condizioni atmosferiche nel futuro, ecc.). In fisica, un esempio di fenomeno aleatorio è quello della determinazione della posizione di un elettrone che ruoti intorno al nucleo di un atomo (in base al "principio di indeterminazione" di Heisenberg, su cui si tornerà). In altri termini, un fenomeno aleatorio o casuale è (o appare) governato dal "caso", piuttosto che da una legge deterministica.
Quando si tratti di fenomeni che evolvono nel tempo, si può anche esprimerne l'aleatorietà dicendo che: "un fenomeno è aleatorio se, pur avendolo osservato con precisione fino al tempo t, non possiamo dire nulla di certo riguardo al suo svolgimento per tempi maggiori di t"; si pensi, ad esempio, all'evoluzione delle condizioni atmosferiche, o a quella della richiesta di potenza elettrica da parte di una data utenza, ecc.: in questi casi possiamo individuare una o più grandezze che descrivono il fenomeno (ad es. la temperatura, la pressione atmosferica, la quantità di precipitazione, e così via nel primo caso; la potenza attiva o reattiva richiesta dagli utenti nel secondo). Detta X(t) una di tali grandezze (oppure un vettore composto di tali grandezze) valutata all'istante t, è chiaro che - pur conoscendo l'intera funzione X(t) dall'istante r all'istante s (con r < s), non possiamo predire il suo valore in qualsiasi istante futuro u, con u > s; ciò vale qualunque sia la scelta di r, s e u. Se invece tale grandezza seguisse una legge nota, ad esempio: X(t) = a + bt (con a e b parametri costanti), il fenomeno sarebbe deterministico (osservando X(t) in un dato intervallo temporale si potrebbero ricavare, con un metodo analitico, le costanti a e b, e quindi predire con esattezza il valore di X(t) in un qualsiasi istante futuro, o anche passato).
Concetti di: "Evento aleatorio" e "Variabile aleatoria"
In termini concettuali (una definizione formale verrà introdotta più avanti) si intende con il termine "evento aleatorio" una proposizione relativa ad un fenomeno aleatorio (ad esempio: fenomeno = "lancio di un dado"; evento = "uscita di un numero pari"), con "prova" l'osservazione di un fenomeno aleatorio. L'evento aleatorio è ben definito se, a seguito della prova, è possibile decidere univocamente se l'evento si è verificato oppure no (nell'esempio precedente, se il risultato del lancio del dado - ossia della "prova" - è il numero due, l'evento "uscita di un numero pari" si è verificato).
Una grandezza numerica è detta "variabile aleatoria" se il suo valore non è noto o calcolabile con esattezza prima della esecuzione della prova, ad esempio: il risultato di un lancio di un dado, prima che tale lancio sia effettuato, il valore che assumerà la temperatura - in un dato luogo - in un istante futuro, l'epoca di appartenenza di un reperto archeologico (si è già notato che la aleatorietà non riguarda solo il tempo futuro!), il numero di reti che saranno realizzate nella prossima partita di calcio "Bologna-Juventus" (oppure: il numero di reti che si sono verificate nella partita di calcio "Bologna-Juventus" del campionato 1962-63, se non ne conosciamo il risultato!), ecc.
Ritornando agli esempi dei fenomeni naturali, si può dire che un fenomeno è aleatorio se una o più grandezze numeriche (temperatura, corrente elettrica, ecc.) che lo descrivono sono variabili aleatorie, o, più in generale, che una variabile aleatoria è una grandezza numerica associata ad una prova di un fenomeno aleatorio (nel caso della partita di calcio del campionato 1962-63, la prova consisterà nella consultazione dei giornali dell'epoca, o di un vecchio album "Panini", o . del sito Internet: "www.juventus.it" !):
Modelli aleatori
Ad una analisi approfondita si può osservare che in realtà tutti i fenomeni in natura sono aleatori, nel senso che non sono mai note o calcolabili con esattezza tutte le grandezze che li descrivono. Operando una distinzione grossolana, possiamo dire che, da un punto di vista pratico, ciò è dovuto all'inevitabile errore di misura che influenza anche fenomeni (supposti) deterministici; da un punto di vista teorico, poi, esiste una aleatorietà intrinseca in ogni fenomeno che risiede nelle nostre limitate capacità di conoscenza delle cause dei fenomeni, soprattutto a livello microscopico.
Esaminiamo dapprima l'aspetto dell'errore di misura. Si consideri l'esperimento consistente nella misura di una resistenza R, tenendo conto che esiste un errore aleatorio (ossia: imprevedibile) di misura, dovuto essenzialmente a: 1) imprecisione degli strumenti, 2) errori di lettura. Sia R il valore vero della resistenza (che noi non conosciamo); se effettuiamo un certo numero n di misure, i risultati non saranno necessariamente gli stessi, ogni misura essendo affetta da un errore aleatorio ei
R1= R+e R2 = R+e R3= R+e .. , Rn= R+en
La grandezza ei rappresenta una "variabile aleatoria", ossia un numero "affetto da incertezza": infatti essa varia casualmente (ossia in maniera imprevedibile) da misura a misura, potendo assumere non un unico valore, ma un insieme di valori in un dato intervallo (ad esempio, l'intervallo (-3,+3 Ohm)). La grandezza R è invece una costante (è sempre la stessa in ogni misura): essa è quindi una grandezza deterministica, sebbene incognita nell'esempio in esame. Di conseguenza, ogni risultato della misura, Ri , risulta essere - prima della effettuazione della misura ! - una variabile aleatoria: anche se conosciamo i valori delle prime n misure, non possiamo prevedere con esattezza il valore della misura successiva. Ad esempio, se R = 20 Ohm, allora il risultato della misura può assumere valori nell'intervallo (-l7,+23 Ohm), anche se naturalmente i valori più lontani da R saranno poco "probabili". Se l'errore fosse nullo o considerato trascurabile, avremmo invece - in ogni misura - il risultato Ri = 20 Ohm, ovvero una grandezza deterministica (rappresentata cioè da un unico valore). Se, ritornando all'esempio precedente, nella applicazione della legge di Ohm teniamo conto dell'errore di misura su tensione e/o resistenza, avremo una incertezza sui valori di V e R che determina una incertezza sul valore di I determinato dalla relazione I=V/R; se, per esempio, la tensione V è nota con certezza, e pari a 100 Volt, la I sarà una grandezza che può assumere valori nell'intervallo (100/23, 100/17 Ampere), e non sapremo quale di questi valori sarà assunto prima di effettuare la misura. In altri termini, I è in questo caso una variabile aleatoria (si noti che, contrariamente a quello che la dizione "variabile" può far pensare, I è - in ogni data misura - costante, e non variabile, ma noi non conosciamo il valore di tale costante prima di effettuare la misura. In altri termini, il termine "variabile" non deve far pensare ad una variabilità nel tempo; del resto, il nostro esempio è relativo ad una corrente continua!).
Esiste poi una aleatorietà intrinseca di molti (in effetti, tutti) fenomeni naturali: a ben vedere, per esempio, anche il passaggio della corrente elettrica in un conduttore è un fenomeno aleatorio: a causa dell'agitazione termica delle particelle, infatti, anche in assenza di tensione applicata esiste una corrente, detta "di rumore", variabile in maniera "irregolare" (casuale) nel tempo e di ampiezza molto piccola, spesso non rilevabile strumentalmente; poiché, in assenza di un campo elettrico applicato dall'esterno, i dipoli elettrici di tali particelle sono orientati casualmente nello spazio, tale corrente è "mediamente" nulla (cioè, se si effettua il calcolo del valor medio temporale di tale corrente su un intervallo di tempo sufficientemente lungo, esso risulta praticamente nullo). Poichè gli strumenti di rilevazione sono sensibili al valore medio della grandezza da misurare, essa risulterà - a meno di non utilizzare strumenti particolarmente sensibili - praticamente nulla. Tale corrente tuttavia esiste, e si sovrappone a quella derivante dalla legge deterministica di Ohm: a rigore perciò, volendo descrivere il più precisamente possibile il fenomeno, dovremmo scrivere:
I = V/R + e
dove e e(t) è una variabile aleatoria, di valore medio nullo, che rappresenta la corrente di rumore nell'istante t considerato. Ciò fa sì che anche la corrente I attraverso il conduttore sia una variabile aleatoria, il cui valore medio temporale coincide con V/R, ma che istante per istante (anche se la tensione è costante!) varia casualmente. Anche se conoscessimo con esattezza il valore di I(t) fino al tempo s, il valore di I(u), in un qualsiasi istante u > s, sarebbe incognito. L'agitazione termica è infatti un fenomeno aleatorio.
Si noti che tale incertezza è indipendente dall'errore di misura: si tratta, appunto, di una incertezza "intrinseca" del fenomeno. Ciò vale per tutti i fenomeni naturali, i quali sono - per effetto della imprevedibilità del comportamento delle particelle elementari - intrinsecamente aleatori, come stabilito nell'ambito della meccanica quantistica, ed efficacemente espresso dal principio di indeterminazione, stabilito dal fisico tedesco Werner Heisenberg nel 1927 (all'età di 26 anni!). Tale principio, espresso in maniera elementare, afferma che non è possibile conoscere con precisione simultaneamente due grandezze che descrivono il moto di una particella. In particolare, detta x la coordinata lungo un certo asse X di una particella, e detta p = mvx la analoga coordinata della quantità di moto, esse possono essere note a meno di un errore, detto dx nel primo e dp nel secondo caso, e che tali errori debbono verificare la disequazione:
dx dp h/2p (1)
dove h è la costante di ck ( h = 6.6262 E-34 Js nel sistema MKSA). Dunque, se aumentiamo la precisione su x, ovvero portiamo a zero il valore di dx, l'errore dp tende all'infinito, e viceversa. Il fatto importante è che questa incertezza è intrinseca, nel senso che non dipende da eventuali errori di misura: essa non può essere eliminata migliorando la tecnica di misura. Da ciò segue, ad esempio, che il moto degli elettroni è intrinsecamente aleatorio, e quindi il passaggio di corrente è un fenomeno aleatorio: in altri termini, non possiamo mai conoscere con esattezza la corrente di "rumore elettrico"; a ciò, che è un fatto teorico , si aggiunge poi il fatto pratico dell'errore di misura.
Se un fenomeno è descritto bene (ossia: con sufficiente approssimazione) trascurandone la aleatorietà, allora è possibile adottare un modello deterministico per un fenomeno aleatorio. Nel caso della legge di Ohm, se la precisione richiesta è accettabile - dal punto di vista ingegneristico - trascurando il rumore elettrico e le indeterminazione sulla misura di V e I, l'equazione V = RI è un modello deterministico che descrive, con buona approssimazione, un fenomeno aleatorio. Ad esempio, nel campo dell'Elettrotecnica, dove sono in gioco correnti di valore molto elevato rispetto a quella di rumore, queste ultime possono essere trascurate. Quando si ha a che fare con correnti molto piccole, ad esempio in alcune applicazioni della Elettronica, invece, ciò non sempre è possibile o opportuno (ad es., ciò è vero in particolare nell'ambito delle comunicazioni elettriche, in cui il "rumore elettrico" va studiato proprio per consentirne l'eliminazione o diminuzione attraverso opportuno "filtraggio"). Come si vede, il fenomeno è sempre lo stesso (passaggio di corrente ), ma il modello adottato è in un caso deterministico, nell'altro aleatorio: è la persona che deve studiare il fenomeno a scegliere quale modello adottare, in base alle sue finalità, alla precisione richiesta, ecc.
Anche la trasmissione su linee elettriche è un fenomeno aleatorio, perché a rigore, si dovrebbero conoscere, ad esempio, con precisione le conduttanze verso terra che tengono conto dell'effetto corona, fenomeno che è complesso da modellare e anche poco prevedibile (essendo legato alle condizioni atmosferiche); tali conduttanze, come è noto, sono calcolate facendo una media su un determinato periodo (si parla infatti di "perdite annue per effetto corona"). In tal modo, si adotta un modello deterministico, perché più semplice di quello aleatorio, ma anche abbastanza accurato. Quando si descrive un fenomeno aleatorio attraverso un modello deterministico, è come se si tenesse conto del solo "valore medio" delle grandezze che descrivono il fenomeno, ritenendo trascurabili le variazioni casuali di tali grandezze rispetto al loro valore medio (come succede appunto nell'esempio delle conduttanze, come in quello della legge di Ohm).
In definitiva, essendo tutti i fenomeni aleatori, quello che interessa è vedere se è possibile adottare un modello deterministico, o un modello aleatorio; quindi è importante fare una distinzione non tra fenomeni, ma tra modelli deterministici e modelli aleatori, tenendo presente che il modello di un fenomeno è sempre una rappresentazione approssimativa del fenomeno stesso. Si consideri ad esempio il caso del lancio di una moneta; l'uscita della "testa" o della "croce" è legata ad un'enorme molteplicità di variabili di tipo meccaniche; il voler descrivere il fenomeno attraverso un modello deterministico, porterebbe a delle complicazioni difficilmente superabili. Per questo motivo, si preferisce descrivere il fenomeno attraverso un modello aleatorio, considerando che, sperimentalmente, dopo un numero di lanci molto grande, la "frequenza" con la quale esce la testa è generalmente pari alla frequenza con la quale esce la croce.
2.2 REGOLARITÀ DEI FENOMENI ALEATORI E "LEGGE DEI GRANDI NUMERI"
Quello appena esemplificato è un esempio di "regolarità" del fenomeno aleatorio "lancio di una moneta". Infatti, molti fenomeni aleatori hanno come caratteristica una certa regolarità, per questo motivo possono essere affrontati con uno studio di tipo matematico, ossia mediante la teoria della probabilità.
Vale infatti la cosiddetta "legge dei grandi numeri" per gli "eventi aleatori", legge che è espressa in maniera elementare di seguito.
Legge dei grandi numeri Dato un evento aleatorio A, per n la frequenza relativa di A in n prove tende ad una costante. Tale costante rappresenta la probabilità che l'evento A si verifichi in una generica prova:
lim Fn (A) = P(A)
n
dove Fn (A) = Sn(A)/n, essendo Sn(A) il numero totale di volte che si verifica l'evento A nella successione di n prove, e P(A) è la "probabilità di A".
Questa è una legge "empirica", in quanto è stata dedotta in passato mediante osservazione diretta dei fenomeni aleatori, ed è infatti detta anche "legge empirica del caso". E' bene sapere che - nell'ambito della teoria della probabilità - la legge dei grandi numeri può essere dimostrata matematicamente, sotto certe ipotesi, ma di ciò per il momento non ci occupiamo, in quanto il nostro discorso è per il momento essenzialmente concettuale e qualitativo.
Ad esempio, essa stabilisce che - se facciamo n lanci di una moneta - la frequenza relativa dell'evento A = "uscita di testa in un generico lancio", tende ad essere sempre più prossima al valore P(A) (ad esempio, 0.5) all'aumentare di n. La regolarità del fenomeno aleatorio sta nel fatto che, benché la frequenza relativa Fn (A) sia una variabile aleatoria, all'aumentare di n essa tende ad una costante. Per chiarire meglio questo fatto, consideriamo tre diverse successioni di lanci di una moneta, e supponiamo, come si fa di solito, che P(A) sia uguale a 0.5 (si noti che questa è una ipotesi, benché appaia "ragionevole": in generale, il valore di P(A) va determinato sperimentalmente);
S1 = (t,t,c,t,c,t..); S2 = (c,c,t,t,t,c.); S3 = (t,t,t,c,c,t.);
si vede che - considerando i primi tre lanci - per S1 è F3(A)=2/3, per S2 è F3(A)=1/3, per S3 è F3(A)=3/3=1; ciò illustra come la frequenza dell'evento, definita in relazione ad una successione di lanci - sia una variabile aleatoria (varia casualmente al variare della successione di lanci). Ciò è naturale, data l'aleatorietà dell'evento; tuttavia, questa imprevedibilità è in un certo senso limitata dal fatto che, pur non potendo dire nulla di preciso sul risultato del lancio, possiamo però dire che Fn(A) tende - come si osserva sperimentalmente - al valore 0.5 per ogni successione. In realtà sarebbe più corretto affermare " per quasi ogni successione", in quanto può accadere (siamo pur sempre nel campo del caso!), se si è "sfortunati", di osservare successioni anomale, ossia fatte di sole teste, di sole croci, ecc., ma queste saranno molto rare (avranno probabilità zero). Quello che qui importa notare è che, mentre la frequenza è una variabile aleatoria, il numero (probabilità di A) a cui essa tende è una costante deterministica (per quanto, spesso, incognita: comunque essa è calcolabile mediante le regole della probabilità, mentre non esiste alcuna "regola" che ci consenta di prevedere il risultato di un lancio, oppure il valore della frequenza di A su un certo numero di lanci).
Un'altro esempio - più interessante dal punto di vista ingegneristico - della regolarità dei fenomeni aleatori è quello della legge probabilistica dell'errore di misura. Torniamo all'esempio dell'errore di misura sul valore di una resistenza: è intuitivo che, in assenza di errori sistematici, si abbia:
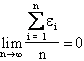
(ossia: la somma degli errori, su un numero elevato di misure, tende ad annullarsi, in quanto gli errori casuali sono con ugual probabilità positivi o negativi, e grosso modo di uguale ampiezza). Si può quindi affermare che il valore vero di R coincide con il valore "medio" relativo ad un numero elevato (teoricamente infinito) di misure. Come si vede, anche in questo caso, benché gli errori siano variabili aleatorie, presentano una certa "regolarità".
In effetti, la teoria degli errori ci consente anche di determinare con quale probabilità gli errori assumono determinati valori: è possibile infatti verificare che l'errore casuale di misura si distribuisce con buona approssimazione secondo una curva di Gauss. Per fissare le idee consideriamo ancora l'esempio della misura di una resistenza il cui valore "vero" è R = 20W, con errore massimo e 3. Supponiamo di effettuare 100 misure di resistenza, ottenendo dei valori misurati di R riportati - per classi - nella seguente tabella:
N. misure Intervallo di valori di R5 17 5 22 10 18 10 21 70 19 |
Il significato dei numeri in tabella è il seguente: 5 misure di R sono comprese nell'intervallo (17-l8 Ohm), altre 5 in quello (22-23 Ohm), etc. La somma del numero di misure è pari a 100, come si vede. Possiamo riportare tali valori su di un istogramma delle frequenze, che riporta, in corrispondenza di ogni intervallo di valori misurati, il numero di misure che cadono in quell'intervallo (. 1a). Ad esempio, risulta che nell'intervallo (19-21 Ohm) cadono 70 misure: possiamo dire dunque che la probabilità che il valore misurato sia compreso in tale intervallo è pari all'incirca al 70%. Per ottenere un valore più esatto di tali probabilità bisogna naturalmente aumentare il numero di misure. Aumentando il numero di misure è possibile restringere le ampiezze degli intervalli: i "rettangolini" che costituiscono l'istogramma diventano sempre più stretti fino ad approssimare sempre di più, quando il numero di misure tende all'infinito, una curva continua.
Generalmente, nei casi come questo in cui l'aleatorietà è dovuta all'errore di misura, è noto che tale curva è rappresentabile con una funzione detta 'Gaussiana" (per la precisione: "funzione densità di probabilità Gaussiana"), in quanto derivata per la prima volta dal matematico tedesco Carl Friedrich Gauss (1777-l855), in relazione ad osservazioni astronomiche. Il nome densità di probabilità deriva dal fatto che l'area sottesa a tale curva in corrispondenza di in certo intervallo fornisce la probabilità di osservare una misura in tale intervallo. Tale curva è rafurata in . 1b.
L'espressione generale della funzione densità di probabilità Gaussiana, in funzione della variabile indipendente x (qui: valore misurato) è:
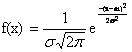 xI ), dove:
m = valore medio (costante reale); s = deviazione standard (costante positiva).
xI ), dove:
m = valore medio (costante reale); s = deviazione standard (costante positiva).
Il valore medio, o "media statistica", m, è il "baricentro" di tale funzione di probabilità, e coincide nell'esempio in esame con il "valore vero" della grandezza da misurare. Il parametro s (deviazione standard) rappresenta la "dispersione" dei valori intorno alla media. In altri termini, all'aumentare della deviazione standard aumenta la probabilità di osservare valori "lontani" dalla media, e quindi, nell'esempio in questione, uno strumento di misura è tanto migliore quanto più s è prossima a zero. Al decrescere di s la curva tende a divenire più alta e più stretta, essendo l'area ad essa sottesa sempre uguale ad 1.
|
s > s |
|
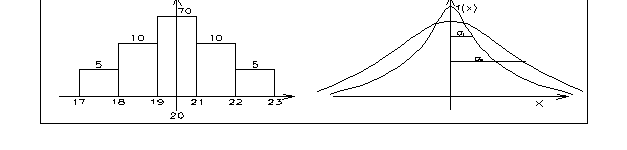
. 1a: Istogramma . 1b: Funzione Gaussiana
Se s tende a zero, la curva tende ad un "impulso" di Dirac centrato sul valore x = m. Questà è l'unica misura che si potrebbe ottenere da uno strumento ideale. La curva Gaussiana è anche detta "Normale", ed è la più utilizzata per la descrizione di molte variabili aleatorie "continue" (dalla altezza delle persone alla intensità del "rumore elettrico").
Questo tipo di esperienze può essere fatto da ogni persona (anche se non ha studiato la probabilità!), ed è appunto sulla base di queste esperienze (soprattutto in relazione ai giochi di azzardo, intorno all 1600) che è nato lo studio della "regolarità" dei fenomeni aleatori attraverso la probabilità.
2.3 - EVENTI ALEATORI E ALGEBRA DEGLI EVENTI.
Si definisce esperimento aleatorio (nel seguito denotato con E) l'osservazione di un qualsiasi processo o fenomeno aleatorio. In altri termini, sulla base di quanto già detto, un esperimento aleatorio (talvolta detto prova) può dar luogo a più risultati, e l'effettivo risultato non è noto a priori. Ad esempio, un esperimento aleatorio può essere il lancio dei dadi, la misura di una corrente, o di una resistenza, la misura della durata di vita di un componente di un sistema ingegneristico, ecc.
Si definisce spazio campione (o "spazio dei campioni", in inglese sample space) l'insieme di tutti i possibili risultati di un esperimento. Esso viene indicato con il simbolo W, mentre con w si denota il generico risultato. Considerato l'esperimento aleatorio "lancio di un dado", si può scrivere: W= per i = 1,,6 se si è interessati all'uscita di una delle 6 facce; se si è interessati all'uscita del pari o dispari, lo spazio campione diviene: W = , con wp = pari, wd = dispari. Se invece si vuol sapere dove cadrà il dado, W coinciderà con l'insieme delle coppie ordinate di numeri reali che individuano il piano su cui può cadere il dado. Dunque, ad ogni esperimento aleatorio possono essere associati più spazi campione; lo spazio campione è in effetti un insieme che dipende dall'osservatore (ossia dagli scopi della sua ricerca).
Si noti anche che in genere il risultato w non è un numero, ma un simbolo (v. esempio del "pari o dispari"); un esempio affidabilistico è il seguente: si tiene in osservazione un componente elettrico per determinare se funzionerà o no, senza guasti, per un anno. Al termine dell'intervallo di osservazione, la risposta sarà "funziona" oppure "non funziona"; volendo, si possono indicare tali eventi con i simboli "zero" e "uno", ma si tratterà appunto di simboli (come le variabili logiche "vero" e "falso") piuttosto che di numeri . Se invece l'osservazione riguarda la misura della durata di vita (cioè "quanto dura" il componente), allora lo spazio campione è formato da tutti i numeri reali non negativi.
Un evento aleatorio A è un sottoinsieme di W (A W), ovvero AIA W), con A W) insieme delle parti di W (l'insieme di tutti i sottoinsiemi di W). Si nota esplicitamente che la definizione (così come il concetto) di evento aleatorio non dipende da quella di probabilità! (che infatti non è stata ancora definita).
Ovviamente, si dice che: l'evento A si verifica quando il risultato wIA; ad esempio, se E = "Lancio di un dado", e A = [Esce un numero pari], se risulta w=2, allora A si verifica perché wIA = (per convenzione, indichiamo tra parentesi quadre una proposizione e tra parentesi graffe gli elementi dell'evento corrispondente). Per definizione, W è detto "evento certo" (perché si verifica sempre), mentre (l'insieme vuoto, ossia l'insieme tale che w wIW) è detto "evento impossibile" (perché non si verifica mai). Ad esempio, nel lancio del dado, detto X il risultato osservato, l'evento [X > 6] non contiene alcun elemento di W, ed è quindi - naturalmente - un evento impossibile. Per una maggiore chiarezza, può essere utile ricorrere ai diagrammi di Venn (v. ura), in cui un insieme è rappresentato da un'area limitata da una curva chiusa ed un elemento dell'insieme è individuato da un punto interno alla linea chiusa.
A
W
Esempio di diagramma di Venn: W = evento certo; A = generico evento; = evento impossibile
Consideriamo un assegnato spazio campione W, e una famiglia di eventi (indicati con A,B, ecc.); possiamo definire per essi diverse operazioni (unione, intersezione, complementazione), di seguito illustrate: l'insieme costituito da W, dagli eventi e da tali operazioni si dice appunto Algebra. Nel seguito, anche dove non espressamente indicato, si supporrà implicitamente che gli eventi considerati appartengano - ovviamente - allo stesso spazio campione.
UNIONE
|
|
L'unione di due eventi A e B, indicata con A B, è un evento che si verifica se si verifica almeno uno dei due eventi A, B: esso cioé si verifica se wIA oppure wIB. La definizione può essere estesa immediatamente a più eventi.
Esempio 1. (d'ora in poi faremo spesso riferimento a questo esempio): Si consideri il lancio di un dado, con W ; se A=[Esce un numero pari] e B=[esce un numero maggiore di 3], allora : A B = ; si nota che l'elemento "4" che appartiene sia ad A che a B va considerato una sola volta, ovviamente, così come il 6.
Esempio 2 (Sistema parallelo in affidabilità). Si considerino due resistenze, a e b, in parallelo tra due nodi di un circuito elettrico. Si suppone che ognuna delle resistenze si possa guastare (a causa, per esempio, di valori di corrente troppo elevati) divenendo un circuito aperto a seguito del guasto. Se il compito di tale sistema è quello di assicurare il passaggio di corrente tra i due nodi, esso funziona se (e solo se) funziona almeno una delle due resistenze. Formalmente, qui lo spazio campione può essere considerato come l'insieme degli stati di funzionamento delle due resistenze (funzionamento normale oppure circuito aperto); detti allora S, A e B gli eventi (aleatori):
S = [Il sistema funziona]; A = [la resistenza a funziona]; B = [la resistenza b funziona], è naturale scrivere (per ora accettiamo intuitivamente il concetto di uguaglianza che è espresso nella relazione che segue; esso sarà definito più precisamente nel seguito):
S = A B.
In generale, un sistema formato da due o più componenti è detto "parallelo" se il funzionamento del sistema richiede il funzionamento di almeno uno dei suoi componenti.
INTERSEZIONE
|
|
L'intersezione di due eventi A e B, indicata con A B, è un evento che si verifica quando si verificano entrambi gli eventi A e B, cioè se wIA e wIB.
Nell'es. 1, A B=
A volte si sente dire, o si legge: "l'intersezione di due eventi è un evento che si verifica quando si verificano contemporaneamente (o simultaneamente) i due eventi": bisogna fare attenzione a interpretare tale tipo di affermazioni, che sembrerebbe indicare che gli eventi devono essere contemporanei, mentre non è così (esempio: A = [ieri ha piovuto], B = [oggi piove] : A B si verifica se piove oggi e ha piovuto anche ieri, ma è chiaro che gli eventi si riferiscono ad intervalli di tempo diversi.)
Esempio 3 (Sistema serie in affidabilità). Si considerino due resistenze, a e b, in serie tra due nodi di un circuito elettrico. Nelle stesse ipotesi dell'es. 2, tale sistema funziona se funzionane entrambe le due resistenze. Formalmente, con la stessa notazione di cui sopra, si ha: S = A B. In generale, un sistema formato da due o più componenti è detto "serie" se il funzionamento del sistema richiede il funzionamento di tutti i suoi componenti. Si noti come anche in questo tipo di definizioni affidabilistiche non compaia la probabilità.
EVENTO COMPLEMENTARE
|
|
Dato un evento A, si dice "evento complementare di A" , e si indica con
![]() (ovvero "A
negato") l'evento che si verifica quando
non si verifica A. Nell'es. 1,
(ovvero "A
negato") l'evento che si verifica quando
non si verifica A. Nell'es. 1, ![]() = . Naturalmente, il complementare dell'evento
certo è l'evento impossibile, e viceversa.
= . Naturalmente, il complementare dell'evento
certo è l'evento impossibile, e viceversa.
IMPLICAZIONE
Dati due eventi, A e B, su uno stesso spazio campione, si dice che "A implica B", e si scrive A B se, quando si verifica l'evento A, si verifica anche l'evento B. In termini insiemistici, ciò equivale a: " A è contenuto in B", ovvero: tutti gli elementi di A sono anche elementi di B. Ciò comporta che l'evento A sia, in un certo senso, più "piccolo" di B, come si vede in ura.
A
W B
Nell'esempio 1, non si ha nè A B nè B A; se invece D = [Esce un numero maggiore di 4], allora D B. Si consideri, come altro esempio, la misura di una corrente I, in Ampere, su un certo conduttore: nel caso più generale, W coincide con l'insieme dei numeri reali; se A = [I > 30] e B = [I > 20], allora A implica B (se si verifica A, si verifica necessariamente B!).
Naturalmente si hanno le evidenti proprietà (valide per ogni coppia di eventi A e B):
A W A B A; A A B (1)
Ad esempio, la seconda delle (1) trova la seguente applicazione affidabilistica: se un sistema serie di due componenti (a,b) funziona, allora funziona necessariamente il componente a (lo stesso vale per il componente b).
Si nota che la definizione non esclude che, essendo A B, sia anche A = B (la definizione di uguaglianza è data appresso), perciò qui non si usa il simbolo
UGUAGLIANZA
Due eventi A e B si dicono uguali, e si scrive A=B, se A B e B A. Infatti in tal caso gli insiemi corrispondenti sono formati dagli stessi elementi. Tornando all'es. 1, in cui A= [X è numero pari], se B = [X è divisibile per 2], allora è chiaro che A=B (se X è pari, allora è divisibile per 2, e viceversa), e infatti A e B sono formati dagli stessi elementi (2,4,6). In generale, la definizione di uguaglianza ora data è più agevole da verificare di quella alternativa (forse più intuitiva): "A e B sono uguali se sono formati dagli stessi elementi", in quanto non obbliga ad enumerare tutti gli elementi di A e B (nell'esempio di prima gli elementi erano solo 3, ma potrebbero essere molti di più, o anche infiniti). Sulla base di tale definizione, si verifica facilmente, ad esempio, che:
A B = B A; A B = B A (proprietà commutativa)
Tale proprietà, analoga a quella della somma o del prodotto per i numeri reali, si estende facilmente a più eventi; ad esempio, per tre eventi:
A B C = A C B = B A C = B C A = C B A = C A B, ed analogamente per l'intersezione. Questa e altre proprietà elementari dell'algebra degli eventi (come la proprietà associativa e quella distributiva,) sono richiamate in Tabella 1, più avanti. Esse sono intuitive, e spesso facilmente visualizzabili mediante i diagrammi di Venn: tuttavia, è bene ricordare che la loro dimostrazione rigorosa va condotta in base alla definizione di uguaglianza appena esposta.
Per chiarire meglio il significato non banale della definizione di uguaglianza, ritorniamo al concetto di "sistema serie". Abbiamo detto, intuitivamente, che un sistema s formato dai componenti a e b è detto "serie" se, con lo stesso significato degli eventi S,A,B prima introdotto, si può scrivere: S = A B. Questo vuol dire due cose, e cioè che (ricordando il concetto di implicazione):
1. (A B) S (se a e b funzionano entrambi, allora funziona s)
2. S (A B) (se funziona s, allora a e b funzionano entrambi)
La 1. afferma che il funzionamento di entrambi i componenti è condizione sufficiente per il funzionamento del sistema; la 2. afferma che il funzionamento di entrambi i componenti è condizione necessaria per il funzionamento del sistema. Dunque, in altri termini, un sistema è serie se: "il funzionamento di tutti i suoi componenti è condizione necessaria e sufficiente per il suo funzionamento". Se si affermasse "un sistema serie funziona se funzionano tutti i suoi componenti" si darebbe una definizione non completa, corrispondente alla sola relazione 1., la quale è vera anche per il sistema parallelo! (se tutti i componenti di un sistema parallelo funzionano, è chiaro che il sistema funziona, e questo è in genere vero per ogni sistema). Bisognerebbe invece aggiungere, al "se" della proposizione precedente, la condizione "e solo se". In effetti è questo che si fa quando di scrive: S = A B, senza tanti giri di parole .
(si consiglia di dare uno sguardo alla Tab.2.3.1 prima di proseguire)
EVENTI INCOMPATIBILI
Se A B = (ossia i due insiemi sono disgiunti, cioé non hanno elementi in comune), gli eventi A e B si dicono incompatibili (infatti non possono verificarsi entrambi). Naturalmente l'evento impossibile è incompatibile con qualsiasi evento. Nell'es. 1, se C = [esce un numero dispari], allora A e C sono ovviamente incompatibili.
Gli eventi A e ![]() sono, naturalmente,
incompatibili (come espresso dall'ultima relazione di Tab. 1)
sono, naturalmente,
incompatibili (come espresso dall'ultima relazione di Tab. 1)
Nel caso di più eventi, essi si dicono incompatibili se lo sono a due a due; ciò vuol dire che al più uno di essi si può verificare. Ad esempio, tre eventi (A,B,C) sono incompatibili se:
A B = ; A C = ; B C = (se si verifica uno qualsiasi dei tre, nessuno degli altri due si può verificare). Naturalmente, ciò implica che anche l'intersezione dei tre eventi sia l'evento impossibile: A B C = (questa proprietà è ovvia: la sua dimostrazione formale può essere effettuata mediante la proprietà commutativa). Nell'esempio dei dadi appena introdotto, con B= [X>3], gli eventi A,B,C non sono incompatibili: infatti, A e C sono incompatibili, ma non lo sono A e B (nè B e C).
|
PROPRIETA' NOTEVOLI DELL'ALGEBRA DEGLI EVENTI Le seguenti proprietà, spesso utilizzate nel seguito, valgono per qualsiasi insieme di eventi (A,B,C..) di un dato spazio campione W
|
Tab. 2.3.1
Nota: Come si vede, la gran parte di tali proprietà è banale, in quanto molto intuitiva. La prima proprietà distributiva (della intersezione rispetto all'unione) è analoga a quella della moltiplicazione rispetto al prodotto per i numeri reali: (a+b)c = ac + bc (questa nota formula può essere utile per memorizzare la proprietà). Si noti che invece che per la seconda non vale tale analogia, in quanto (a+b)c non è uguale a: (a+c)(b+c).
Proprietà notevoli della implicazione
Si supponga che A B; si verificano allora facilmente (ad esempio mediante i diagrammi di Venn) le seguenti notevoli proprietà:
A B =
B; A B = A; ![]()
![]() (2)
(2)
(la terza si può dimostrare per assurdo). Si noti che valgono anche le relazioni inverse: cioè, se una qualsiasi delle (2) è vera, allora A B. Quindi, l'unione o l'intersezione possono essere utilizzate per definire l'implicazione.
Applicando la terza delle (2) alla prima delle (1), si ha anche che : "l'evento impossibile implica ogni altro evento", affermazione che può apparire strana, dato che l'evento impossibile non si verifica mai! (la si può comprendere pensando che l'evento impossibile è il "più piccolo" evento dello spazio campione, ed è dunque contenuto in ogni altro evento).
DIFFERENZA
|
|
L'evento differenza "A meno B", indicato con AB, è un evento che si verifica quando A si
verifica e B non si verifica. In altri termini, esso è costituito dagli
elementi di A che non appartengono a B. Si ha la notevole proprietà: AB = A ![]() . Nell'esempio 1, AB = . Infatti A= e B = : "togliendo" da A gli elementi 4 e 6 che sono
anche in B, si ha l'evento "A meno B" (alternativamente, si può operare
l'intersezione tra A e il complementare di B: farlo per esercizio).
. Nell'esempio 1, AB = . Infatti A= e B = : "togliendo" da A gli elementi 4 e 6 che sono
anche in B, si ha l'evento "A meno B" (alternativamente, si può operare
l'intersezione tra A e il complementare di B: farlo per esercizio).
TEOREMA DI DE MORGAN
Tale importante teorema stabilisce le seguenti identità:
![]() ;
; ![]() (3a)
(3a)
Anche esse vanno dimostrate mediante la definizione di uguaglianza. Tuttavia, è semplice verificarle intuitivamente; ad esempio, la prima afferma che l'evento "non si verifica almeno uno degli eventi A e B" è uguale all'evento "non si verifica nè A nè B". Un chiaro corrispondente affidabilistico di tale affermazione è: "un sistema parallelo non funziona quando (se e solo se) non funziona nessuno dei suoi componenti", affermazione che appare di immediata comprensione.
Analogo ragionamento vale per la seconda relazione, che può essere interpretata affidabilisticamente come segue: "un sistema serie non funziona quando (se e solo se) non funziona almeno uno dei suoi componenti". Il lettore è invitato a verificare la validità di tali relazioni anche mediante un esempio con i diagrammi di Venn.
Il teorema di De Morgan può essere facilmente generalizzato a più eventi come segue:
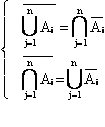 (3b)
(3b)
Spesso, come vedremo, è utile esprimere un evento mediante l'unione di
eventi incompatibili; esempi notevoli di tali decomposizioni sono le seguenti,
valide per ogni coppia di eventi A e B; in entrambe e l'evento
differenza AB = A ![]()
A = (A B) (AB) (4a)
A B = B (A B) (4b)
Anche esse possono essere facilmente visualizzate mediante i diagrammi di Venn.
Se si vuole dimostrare, ad esempio, la prima relazione, il modo più semplice è il seguente:
A = A W = A (B ![]() ) = (A B) (A
) = (A B) (A ![]() ), da cui l'asserto.
), da cui l'asserto.
Si noti che, come detto, in entrambi i casi a secondo membro appare l'unione di eventi incompatibili come si vede subito dal diagramma di Venn, e si può dimostrare mediante la proprietà associativa.
Nota: Su alcuni testi, l'operazione di unione (o "somma logica") è indicata con il simbolo +, quella di differenza con il simbolo -, quella di prodotto con il puntino, ecc., come per i numeri reali. Ciò è naturalmente lecito, purché non si faccia confusione con le corrispondenti operazioni valide per i numeri. Un esempio di tale confusione lo offre la (4b) che, secondo tale simbologia alternativa andrebbe scritta: A + B = B + (A-B): a questo punto, sarebbe un errore "semplificare", come si potrebbe fare con i numeri, al secondo membro i termini B e -B: ne risulterebbe: A + B = A, mentre la relazione: A B = A chiaramente non vale sempre (quando è valida?). Si noti invece che la (4b) vale sempre !.
|
Privacy
|
© ePerTutti.com : tutti i diritti riservati
:::::
Condizioni Generali - Invia - Contatta