modulo IV

Le variabili aleatorie

4.1 DEFINIZIONE DI VARIABILE ALEATORIA (v.a.)

Il concetto di variabile aleatoria (v.a.) è stato già introdotto inizialmente (par. 2.1). Qui lo si definisce in maniera un po' più formale; dal punto di vista delle applicazioni affidabilistiche, le v.a. trovano la maggior parte delle applicazioni nella "analisi dinamica" (cap. 6), per cui il lettore interessato alle applicazioni può anche leggere questo modulo dopo il cap. 5 (che utilizza essenzialmente i metodi del Cap. 2,e qualche risultato del Cap. 3).

Con il calcolo delle probabilità, si sono definiti gli eventi come possibili risultati di un determinato esperimento aleatorio; ad ogni evento si è poi associato un numero, detto probabilità dell'evento, che in un certo qual modo quantifica "l'attitudine" di un evento a verificarsi.

Per facilitare la manipolazione dei dati, è utile introdurre una corrispondenza che associ gli eventi di un determinato esperimento aleatorio all'insieme dei numeri reali, A, in modo da poter considerare come risultati possibili di un esperimento aleatorio non più gli eventi stessi, ma i numeri reali ad essi associati. Si introduce, in tal modo, il concetto di variabile aleatoria.

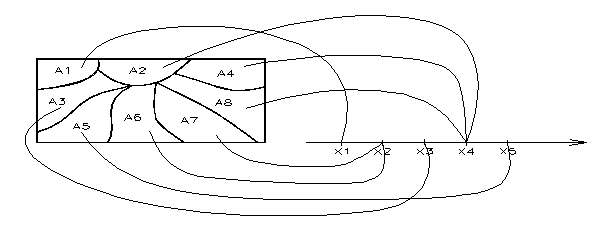
Una variabile aleatoria (v.a.) è una legge che associa ad ogni evento un numero reale; in termini matematici, una variabile aleatoria è una "funzione reale misurabile" definita sullo spazio campione. Detto, quindi W lo spazio campione, la variabile aleatoria è una funzione definita in

A W) ed a valori in A, che rappresenta il "codominio" di tale applicazione (. 1).

In pratica, una v.a. è un numero incognito, ovvero rappresenta un insieme di possibili numeri.

Esempi di vv.aa. sono:

1) La v.a. "indicatrice" , diciamo X_A, di un evento A di un dato spazio campione, ossia una grandezza che vale 1 se A si verifica, 0 se A non si verifica: evidentemente tale v.a. associa a tutti gli elementi di A il numero reale 1, a tutti gli elementi del complementare di A il valore 0. Qui il codominio di X_A è semplicemente l'insieme binari (0,1), che è un particolare sottoinsieme dei numeri reali. Chiaramente, se vogliamo sapere se "la v.a. X_A vale 1", ci stiamo chiedendo se A si verifica;  quindi la proposizione [X_A=1] equivale all'evento A, (infatti X vale 1 se e solo se A si verifica);

2) ancora con riferimento ad un esperimento "binario" (per il quale ci interessi cioè solo sapere se un dato evento A si verifica oppure no), se vinciamo una certa somma, p.es. 100 lire se A si verifica, e nulla altrimenti, la vincita - prima di effettuare l'esperimento - è chiaramente una v.a., che vale 0 oppure 100; se la indichiamo con Y, si può scrivere Y = 100X_A , essendo X_A l'indicatrice di A;

3) Il risultato di un lancio di un dado, visto come numero (e non come simbolo!) è una v.a. con spazio campione formato dalle sei facce del dado (f₁,..f₆) e codominio (1, . 6), coincidente con i primi 6 numeri naturali, ovvero il numero di puntini scritti su tali facce. Ma se siamo interessati al fatto che esca un numero pari, potremmo introdurre la v.a. indicatrice di tale evento, diciamo Y. In tal caso, Y è un'altra v.a. (essendo una grandezza numerica) definita sullo stesso spazio campione, ma a valori in (0,1). Essa associa agli elementi (f₂,f₄,f₆) il valore 1, agli elementi (f₁,f₃,f₅) il valore 0; si nota come ad uno stesso numero del codominio (ad es. 1), corrispondano in genere più eventi dello spazio campione (ad es., in questo caso, gli eventi: (f₂); (f₄); (f₆); (f₂,f₄,f₆), l'evento (f₂,f₄), ecc.

Si osserva che, come in questo esempio, la corrispondenza tra A W) e A non deve essere necessariamente biunivoca. Ciò succede anche in . 1: ad esempio la variabile aleatoria associata agli eventi A₂, A₄, A₈, assume sempre lo stesso valore x₄, e la variabile aleatoria associata agli eventi A₆, A₇ assume sempre lo stesso valore x₂.

I prossimi esempi sono di interesse affidabilistico (ma in effetti potrebbe esserlo anche l'Es. 1), se l'evento A rappresenta il "buon funzionamento di un dato sistema"). Si darà indicazione del codominio delle v.a. in esame, lasciando al lettore di individuare il dominio, ossia lo spazio campione (si noterà che comunque - dal punto di vista pratico - la corretta individuazione del dominio non è essenziale) .

4) Si consideri un sistema formato da n componenti, ed un dato intervallo di tempo: il numero di componenti di tale sistema che funzionano ininterrottamente nell'intervallo di tempo è una v.a., con codominio l'insieme: (0,1, . n);

5) Il numero di manovre che un interruttore compie nella sua durata di vita (ossia prima del suo "guasto") è una v.a., con codominio l'insieme dei numeri naturali (0,1, . n, . ); si noti che - per lo meno teoricamente - il codominio non è limitato superiormente.

Gli esempi visti finora sono relativi a vv. aa. discrete, ossia con codominio discreto (anche se possibilmente infinito, come nell'Es. 5); i prossimi riguardano vv. aa. "continue" (il codominio ha la potenza del continuo).

6) il tempo di funzionamento di un dato componente  è una v.a., a valori in A

In effetti, ciò è vero anche per la durata di vita di un qualsiasi organismo vivente (animale, pianta, essere umano), o per la durata di gran parte dei fenomeni naturali o sociali (durata di un temporale, di una guerra, di una telefonata, ecc.);

7) il "carico" di un sistema elettrico (ossia il valore potenza elettrica richiesta dall'insieme degli utenti del sistema) in un dato istante di tempo futuro è una v.a., a valori in A

Se si considera il carico in un intervallo, anziché in un istante, di tempo, si ha a che fare invece con un "processo" aleatorio , ossia una funzione aleatoria del tempo, in parole povere una grandezza che varia nel tempo, e che in ogni istante è descritta da una v.a.; il "processo" è dunque descrivibile come un "insieme" di vv. aa., ed è una grandezza un po' più complessa di una semplice v.a.

Se si considera però la "punta di carico" del sistema nell'intero intervallo, si ritorna invece ad una v.a. (essa infatti rimane costante - benchè incognita -  all'interno dell'intervallo).

Come si può capire in base a quest'ultimo esempio, il nome "variabile" non deve far pensare ad una variabilità temporale (si riveda anche quanto detto nel Cap. 2, . 4, a proposito di una corrente continua di valore incognito); quando fu assegnata tale denominazione, si era in epoca "frequentista", per cui si pensava ad una grandezza che variava ad ogni ripetizione dell'esperimento (come il risultato di successivi lanci di un dado). In effetti, quando si ha a che fare con esperimenti non ripetibili (cioè quasi sempre), o con una incertezza di carattere soggettivo, la v.a. è una costante incognita, e non varia, affatto, come nei seguenti esempi:

8) l'anno di nascita di un certo personaggio storico, per chi non l'abbia studiato o non lo ricordi, è una v.a. (a valori nell'insieme dei numeri naturali che individuano i possibili anni di nascita);

9) la 1000-sima cifra dopo la virgola del numero reale "pi greco" è - per chi non non lo conosca (quasi tutti, probabilmente) - una v.a., a valori nell'insieme (0,1, . , 9); probabilmente, se una qualsiasi persona dovesse indovinare di che cifra si tratta, attribuirebbe a tutte e 10 la stessa probabilità di 1/10 ( e farebbe bene), anche se teoricamente potrebbe calcolarla con certezza . In ogni caso, è chiaro che essa è una costante!

A ben vedere, il valore "esatto" - espresso in base decimale - del numero p, visto come numero reale è da considerarsi aleatorio anche "oggettivamente" - anche se p viene fuori da una formula deterministica! - in quanto non esiste alcuna formula che ci consenta di calcolare le successive cifre della sua espansione decimale, pur essendo note tutte le precedenti. Ogni tanto c'è qualche studioso, in genere giapponese . , che si "diverte" a calcolare un numero sempre maggiore di cifre decimali (un certo Kaneda, dell'Università di Tokyo, arrivò nel 1987 a calcolare p fino a 10⁸ cifre), ma il procedimento potrebbe continuare all'infinito, mentre i nostri tempi sono inevitabilmente finiti, e quindi il numero è aleatorio e, chiaramente, costante!

Gli ultimi esempi mostrano come la dizione "variabile aleatoria" possa essere fuorviante (i seguaci della concezione soggettiva utilizzano spesso il termine "numero aleatorio").

Si nota, infine, che il concetto di v.a., come quello di evento aleatorio, è indipendente da quello di probabilità

4.2 DISTRIBUZIONE DI PROBABILITA' DI UNA V.A.

Nel seguito, si indicherà con (X = x_A) l'evento A tale che, per ogni punto di A, si abbia: X = x_A

Per convenzione, la vv.aa. sono indicate con lettera maiuscola, i loro possibili valori con lettera minuscola.

In genere, ci interesserà calcolare la probabilità con cui una data v.a. assuma i possibili valori del suo codominio; questo è possibile una volta noti i valori di probabilità degli eventi dello spazio campione (si noti che quando  scriviamo P(X = 3), oppure P(X > 1), ecc., ci riferiamo comunque alla probabilità P( ) definita sul dominio , anche se apparentemente l'evento è definito in termini di codominio).

Con riferimento alla . 1 del par. precedente, si può costruire la seguente tabella:

Da un punto di vista formale, si può scrivere:

P(A₁) = P(X=x₁) P(A₁)= p₁

P(X=x₂) = P(A₆ A₇) = p₆ + p₇

P(X=x₃) = P(A₃) = p₃

P(X=x₄) = P(A₂ A₄ A₈) = p₂ + p₄ + p₈

4.2. 1. Variabili aleatorie discrete.

L'associazione di un evento ad un numero reale è assolutamente arbitraria, quindi, si comprende che la variabili aleatorie sono infinite, esistendo infiniti eventi.

Come esemplificato, le variabili aleatorie si dividono in discrete e continue, a seconda della "potenza" del codominio.

Nel caso di vv.aa. discrete, si dice "legge di distribuzione di probabilità" (in breve: "ldp") di una v.a. X, la funzione che associa ad ogni possibile valore di X la probabilità con cui essa assumere tale valore; essa è dunque una funzione reale di variabile reale, definita da:

p_X(x) = P(X = x) (1)

La legge di probabilità può essere espressa a mezzo di una tabella del tipo:

dove gli x_i sono i valori discreti che la variabile aleatoria può assumere e p_i sono le probabilità P(X=x_i).

Naturalmente, deve essere:

p_i 0 e (2)

La distribuzione di probabilità può essere riportata su un grafico (. 2).

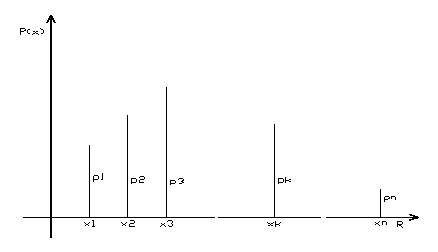
4.2.2 Variabili aleatorie continue

Una v.a. X è continua se i valori che essa assume sono contenuti in un intervallo reale.

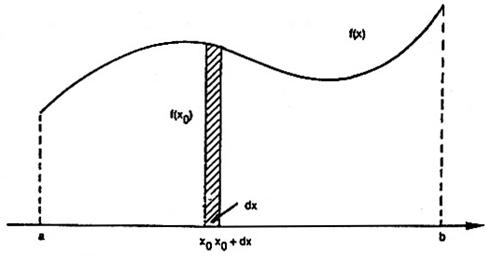
Per le v.a. continue non è possibile ottenere una rappresentazione equivalente a quella delle v.a. discrete perché, in tal caso, non è possibile elencare i valori che essa assume e , quindi, attribuire a ciascuno di essi le corrispondenti probabilità. Il problema si risolve associando a ciascun punto dell'intervallo su cui è definita la v.a. una funzione f(x), detta funzione densità di probabilità ("fdp"), tale che, per ogni x₀I(a,b) si abbia (v. . 3):

f(x₀)dx = P(x₀ X x₀+dx) (3)

Si noti che la fdp non è una probabilità, anche dal punto di vista dimensionale; ad esempio, se la v.a. X è un tempo, la dimensione di f(x) sarà del reciproco di un tempo; quindi il valore di f(x) dipenderà dall'unità di misura scelta (sec^-l, ore^-l, ecc); da ciò segue, ad esempio, che la fdp potrà anche assumere - a differenza di una probabilità - valori maggiori di 1!

Tramite la (3), nota la f(x), si può calcolare la probabilità di qualsiasi evento utilizzando le nozioni

elementari del calcolo integrale. Ad esempio, volendo calcolare la probabilità che la X assuma un valore compreso nell'intervallo (c,d), basterà integrare la f(x) da c a d. Pertanto si avrà (. 4):

relazione da cui appare chiaro il significato del nome di "densità".

La funzione densità di probabilità gode delle seguenti - intuitive - proprietà:

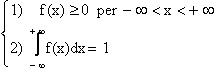che sono le equivalenti delle: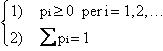

del caso discreto, quando alle p_i si sostituiscono le quantità f(x_i)dx e al simbolo a il simbolo

Valgono le seguenti proprietà:

La probabilità che una v.a. continua assuma un qualunque valore x₀ è sempre 0; infatti,

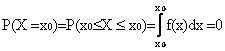
Quindi, ad esempio, la probabilità che una v.a. continua assuma un valore razionale è zero! (perché?). Analogamente, la probabilità che una v.a. continua assuma un valore irrazionale è 1 (i due eventi sono infatti complementari).

(5)

(6)

Si definisce funzione di distribuzione di probabilità (in breve "FDP") si indica con F(x) la seguente funzione:

(7)

Valgono le seguenti proprietà:

F(x) è funzione crescente di x    (8a)

Infatti, se a < b, l'evento (X < a) implica l'evento (X < b));

F(- ) = P(x ) = 0 (8b)

F(+ ) =P(x (8c)

Da F(x) è deducibile la probabilità di un qualsiasi evento relativo ad intervalli, infatti:

P(a X <b ) = F(b)- F(a) (9)

Si osservi la FDP può essere definita anche per una v.a. discreta con valori x_i:

F(x) = P(X x) =ap_i

con sommatoria estesa a tutti i valori x_i non superiori ad x. E' facile vedere che il grafico di tale funzione sarà "a gradini" (funzione costante a tratti).

4.3 MEDIA STATISTICA DI UNA VARIABILE ALEATORIA

E' molto utile introdurre dei parametri (deterministici!) che possano fornire un'indicazione sintetica dei possibili valori assunti da una v.a., senza esaminare l'intera distribuzione o densità di probabilità. I più importanti sono definiti di seguito.

Il "valore medio" (o: "media statistica", o: "valore atteso", o: "speranza matematica") di una v.a. X si indica con il simbolo E[X o ,e rappresenta, dal punto di vista frequentista, la media aritmetica dei valori che una v.a. assume in un gran numero di prove. Esso si ottiene come media pesata dei valori assunti per le rispettive probabilità, e rappresenta il valore della v.a. X attorno al quale la distribuzione "si accentra", ovvero il "baricentro" della ldp o della fdp.

Data una v.a. discreta X definita su W ed a valori (x₁,x₂,,x_n)IA risulta per definizione:

m 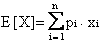(1)

Allo stesso modo, per una v.a. continua si ha:

Facendo un'analogia con la meccanica, il valore medio, per come è stato definito, è assimilabile al baricentro di una distribuzione di masse. In altre parole, E[X] rappresenta il momento di un sistema costituito da n "masse" p_i ( i = 1,..,n), poste ad una "distanza" x_i da un "polo"; per tale motivo, E[X] è anche detto momento primo della distribuzione.

La funzione E[ ] è un operatore lineare e gode delle seguenti proprietà:

E[c] = c; con c = costante;

E[c X] = c E[X];

E[a+b X] = a+b E[X];

4. se P(a < X < b) = 1, allora: a < E[X] < b.

4.4 MEDIA DI FUNZIONI DI VARIABILI ALEATORIE. MOMENTI SUPERIORI.

Se X è una v.a. definita su un certo spazio campione W, e g è una funzione definita su A, è chiaro che y = g(x) è ancora una v.a.. Ad esempio, se R è la v.a. "Resistenza di un dato elemento di un circuito", e v è la tensione (supposta nota, cioè deterministica) applicata a tale elemento, la corrente I = v/R, che fluisce in esso, è una v.a che si ottiene applicando la funzione g(r) = v/R alla v.a. R.

Per calcolare il valore atteso di tale funzione, è utile la seguente proprietà (intuitiva) che permette di calcolare la media di y = g(x) senza far ricorso alla sua legge di probabilità:

(se X è continua)

(se X è discreta)

Si possono, a questo punto, introdurre i momenti superiori di una v.a. Si definisce momento di ordine r di una v.a. la grandezza

(2)

dove il secondo membro deriva dalla 1); infatti m_r è la media della v.a. Y = X^r

Tramite il momento primo, si costruisce la v.a. scarto rispetto alla media definita dalla relazione:

Y = X - m

Si deduce, quindi, che i momenti delle v.a. Y sono misure di variabilità rispetto alla media, per cui si definiscono i momenti della v.a. scarto, che si indicano con e valgono:

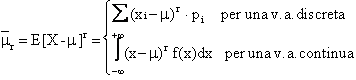(3)

Tra questi il più importante è il momento secondo rispetto alla media che prende il nome di varianza ed è indicato con s o con Var(X):

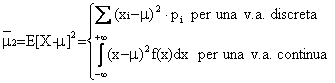(4)

Vale la seguente proprietà che discende dalla linearità di E[X]:

Var(X) = E[(X - m)]² = E[X²]- E²[X] = m m (5)

Ovvero: la varianza è uguale al momento secondo meno il momento primo al quadrato. Si noti che E[X²] E²[X]; in generale, infatti, se g(x) non è una funzione lineare, si ha E[g(x)] g[E(X)]; dal fatto che deve essere Var [X] 0 (perché?), si ricava, anzi, che E[X²] > E²[X].

In effetti Var [X] > 0 sempre, eccetto nel caso in cui X è costante, caso in cui Var(X) = 0; in tal caso si dice che la v.a. coincide "quasi certamente" con il suo valore medio.

La varianza, in definitiva, è un parametro collegato all'ampiezza della curva e indica la dispersione intorno alla media.

Si definisce deviazione standard (standard deviation) e si indica con D(X) o s la radice quadrata positiva della varianza; a volte s è detto scarto quadratico medio.

E' bene sottolineare che i momenti sono indicatori sintetici di una v.a. e quindi non esauriscono la conoscenza della sua distribuzione; tuttavia, conoscendo media e varianza di una distribuzione, è possibile in alcuni casi particolari (ad esempio, per una distribuzione Gaussiana) ricavare la funzione di distribuzione stessa.

Esistono numerosi altri parametri per sintetizzare una v.a. in analogia con quelli appena visti; i più importanti sono la moda e la mediana.

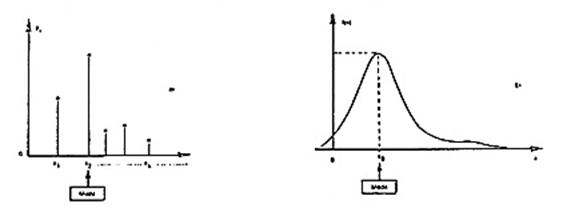
La moda è il valore in cui è massima la ldp (per una v.a. discreta) o la fdp (per una v.a. continua); talvolta si dice che esso è il valore più probabile di una v.a. (ma ciò nel caso continuo non è vero, in

quanto ogni valore in tal caso viene assunto con probabilità zero!); la . 1 mostra come può essere determinata.

La mediana è quel valore per cui la funzione di distribuzione vale ½ , cioè vale ½ la probabilità che la v.a. superi la mediana, o che sia inferiore alla mediana (. 2).

4.5 ESEMPI DI DISTRIBUZIONI DI VARIABILI ALEATORIE DISCRETE.

In questo paragrafo e nel successivo verranno analizzate alcune particolari famiglie di vv.aa. utili da un punto di vista applicativo.

Le distribuzioni delle vv.aa. prese in considerazione sono tutte funzioni di uno o più parametri, cioè di determinate quantità che le caratterizzano. Se è noto dunque che un certo fenomeno aleatorio è descritto da una v.a. appartenente ad una determinata famiglia, per poterlo descrivere completamente dal punto di vista probabilistico, è necessario solo individuare il valore assunto dai parametri di quella famiglia.

4.5.1 Variabile aleatoria Binomiale

La variabile aleatoria binomiale è utilizzata ogni qual volta l'esperimento aleatorio in esame può essere ricondotto ad una prova che genera solo due eventi incompatibili del tipo successo-insuccesso; è quindi, una v.a. discreta. Sia n il numero di prove, p la probabilità che la prova abbia avuto esito favorevole e q = 1-p la probabilità che la prova abbia avuto esito sfavorevole; se le prove sono indipendenti, la variabile aleatoria X = "numero di successi in n prove" segue una ldp detta binomiale, e si scrive X B(n,p); mediante il calcolo combinatorio e l'ipotesi di indipendenza, si dimostra che essa ha la seguente legge di distribuzione di probabilità:

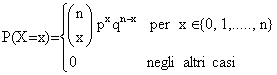(1)

Esempio 1: Si calcoli la probabilità che effettuando 3 lanci di una moneta escano 2 teste.

Detta X la variabile aleatoria associata all'evento "escono x teste", considerando che n=3, p=q=1/2 la P(X=1) sarà:

risultato che si può verificare anche con enumerazione diretta dei casi possibili e favorevoli (ma questo solo perché p=1/2, e dunque vale l'equiprobabilità di tutte le possibili terne di risultati).

Esempio 2 Si calcoli la probabilità di ottenere 5 teste su 10 lanci, e si verifichi che non vale ½.

Esempio 3 Dato un sistema di generazione formato da 3 generatori in parallelo, tutti di taglia 10 MW, di uguale affidabilità - nel periodo di un anno - pari a 0.95, si calcoli la probabilità che il sistema fornisca senza interruzioni nell'anno in esame almeno 20 MW.

La distribuzione di probabilità vista è detta binomiale perché la somma dei suoi termini per x variabile da 0 a n, rappresenta lo sviluppo del binomio di Newton.

La binomiale gode delle seguenti proprietà:

la distribuzione di probabilità prima cresce e poi decresce per cui in generale è unimodale;

la media e la varianza sono pari rispettivamente a:

E[X] = n p   Var[X] = n p (1-p) (2)

4.5.2 Variabile aleatoria di Bernoulli, o "Indicatrice di un evento"

La v.a. indicatrice di un evento A, detta anche v.a. di Bernoulli, è una particolare v.a. Binomiale in cui n=1 e p = P(A). In altre parole, la v.a. segue una ldp B(1,p), e la sua legge distribuzione di probabilità è la seguente:

E' facile dimostrare che E[X^r]=p r = 1,2, da cui deriva, in particolare, che:

E[X] = p Var[X] = p(1-p) (4)

La prima  si dimostra applicando la definizione di valore medio:

E[X] = a x_i p_i = 0 p⁰ (1-p)¹ + 1 p¹ (1-p)⁰ = p

La seconda delle (4) si dimostra nel seguente modo:

Var (X) = E[X²] - m = E[X²] - p²; ma E[X²] = E[X] = p, quindi Var [X] = p-p² = p(1-p).

Derivando Var[X] e uguagliando a zero si vede che la varianza per una v.a. di Bernoulli ha un massimo per p = ½ e tale massimo vale 1/4.