APPENDICE #1

La linearizzazione di funzioni di una sola variabile

Consideriamo la trasformazione non lineare y=g(x). La linearizzazione nell'intorno di un punto x₀ di tale funzione consiste nel sostituire l'espressione della g(x) con quella della retta tangente il grafico y=g(x) della funzione in corrispondenza del punto (x₀, g(x₀)).

Il punto generico sulla retta tangente, detta a_t la tangente dell'angolo a che essa forma con l'asse delle x (tga_t =a), avra' coordinate (x,y=g(x₀)+a_t (x-x₀)).

Il valore a_t (coefficiente angolare) della retta e' pari a quello che la derivata prima della funzione g(x) assume nello stesso punto.

La retta tangente si puo' pensare ottenuta a partire dalla retta secante, passante per i punti (x₀,g(x₀)) e (x,g(x)), al tendere di x a x₀.

Il coefficiente angolare di tale retta e' pari a

 

e quello della retta tangente si ottiene da questo al tendere di x a x₀:

In maniera del tutto analoga si ricava l'espressione linearizzata di una funzione di due variabili g(x,y) nell'intorno del punto (x₀,y₀). Essa consiste nella sostituzione di g(x,y) con l'espressione del piano tangente nel punto (x₀,y₀) alla superficie z=g(x,y).

Il punto generico sul piano tangente avra' coordinate (x,y,z= g(x₀,y₀)+a_1t(x-x₀)+a_2t(y-y₀)), con a_1t l'inclinazione della retta ottenuta intersecando il piano tangente con il piano coordinato di equazione y=0 e a_2t l'inclinazione della retta ottenuta intersecando il piano tangente con il piano coordinato di equazione x=0.

I coefficienti angolari di tali rette sono pari rispettivamente alla derivata parziale di g rispetto a x, calcolata nel punto di linearizzazione e alla derivata parziale di g rispetto a y, sempre nello stesso punto.

Il piano tangente infatti si puo' pensare ottenuto dal piano secante la superficie nei punti (x₀,y₀,g(x₀,y₀)), (x,y₀ ,g(x,y₀)) e (x,y,g(x,y)), al tendere di x a x₀  edi y a y₀.

L'equazione del piano secante e' data da

dove

Quella del piano tangente sara'

dove

Se ordiniamo le coordinate x,y di un generico punto del piano in un vettore  , possiamo scivere l'equazione di un piano nella seguente forma matriciale:

.

La matrice A  contiene i coefficienti angolari delle rette ottenute intersecando il piano rispettivamente con il piano coordinato di equazione y=0 e con quello di equazione x=0.

L'ordine con cui scrivo tali coefficienti nella matrice dipendera' da quello con cui ordino le coordinate x,y nel vettore x.

L'equazione del piano tangente in forma matriciale sara'

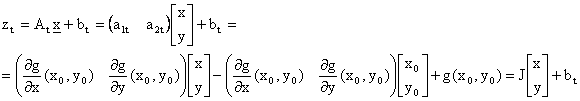
dove

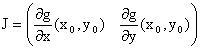
si chiama matrice Jacobiana della trasformazione g(x,y), qui calcolata nel punto (x₀,y₀).

Consideriamo infine il caso di una trasformazione a valori vettoriali.

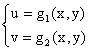
In questo caso si trattera' di linearizzare separatamente le due componenti g₁ e g₂ in corrispondenza del punto (x₀y₀). Avremo

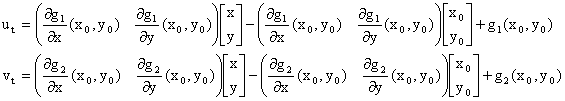
che puo' scriversi come

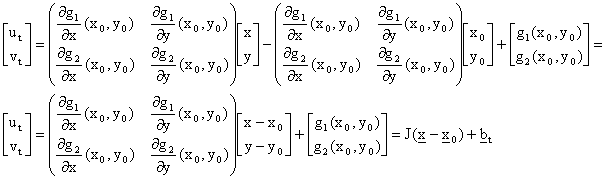
In questo caso la matrice jacobiana ha 2 righe, la prima contenente le derivate parziali dalla componente g₁ e la seconda quelle della g_2.