associativa - elemento neutro - inverso

Def. Un insieme , su cui sia fissata un'operazione (ovvero una applicazione, una funzione):

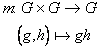
è detto gruppo se l'operazione gode delle seguenti proprietà:

1) associativa: ;

2) elemento neutro: : tale che ;

3) inverso: in corrispondenza ad ogni elemento , , tale che .

Def. Il gruppo si dice gruppo commutativo (o abeliano) se in più vale :

4) commutativa :

Def. Un insieme , su cui siano fissate due operazioni (ovvero due applicazioni, due funzioni),

dette somma e prodotto:

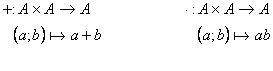
è detto anello se valgono le seguenti proprietà:

1) associativa per la somma : ;

2) elemento neutro per la somma : tale che ;

3) opposto: in corrispondenza ad ogni elemento tale che ;

4) commutatività per la somma : ;

5) associatività per il prodotto : ;

6) proprietà distributive :

Def. Un anello si dice con unità, se vale anche:

7) elemento neutro per il prodotto : tale che

Def. : Un anello si dice commutativo, se vale anche:

8) commutatività per il prodotto :

Def. : Si dice che un anello è anello a divisione (o corpo), se è anello con unità e in più vale:

9) inverso : in corrispondenza ad ogni elemento , tale che:

Def. : Un anello commutativo a divisione si definisce campo. (In pratica è un campo se sono

soddisfatte le condizioni 1-9).